人教A版数学必修二2.2.3 直线与平面平行的性质 教案
文档属性
| 名称 | 人教A版数学必修二2.2.3 直线与平面平行的性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 228.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 00:00:00 | ||
图片预览

文档简介
2.2.3 直线与平面平行的性质
一、教学目标:
1、知识与技能:掌握直线与平面平行的性质定理及其应用。
2、过程与方法:学生通过观察与类比,借助实物模型理解性质及应用。
3、情感态度与价值观:进一步提高学生空间想象能力、思维能力;体会类比的作用;渗透等价转化的思想。
二、教学重、难点:
重点:直线与平面平行的性质定理的理解。[来源:学科网]
难点:直线与平面平行的性质定理的证明及正确运用。
三、学法指导:学生借助实物,通过类比、交流等,得出性质及基本应用。
四、教学过程:
(一)复习回顾
复习:(1)直线与平面平行的判定定理:。
(2)平面与平面平行的判定定理:
师生活动:教师提问,首先叫一个同学来回顾,然后让其他同学来补充完善。
答案:(1)不在平面内的一条直线与平面内的一条直线平行,则这条直线与这个平面行
(2)一个平面内的两条相交直线分别与另一个平面平行,则这两个平面平行
本质:线线平行推出线面平行,由线面平行可推出面面平行
(二)研探新知
问题1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?
师生活动:教师提问,学生思考回答。平行、异面
问题2:若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?
师生活动:教师提问,学生思考回答。无数条,平行
问题3:如何在平面α找到这些与直线a平行的直线?
师生活动:教师提问,学生思考回答。过直线a作平面
问题4:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?
师生活动:教师提问,学生思考回答。平行或相交
问题5:直线a与平面平行,过直线a的某一平面,若与平面相交,则交线与直线a有什么样的位置关系?
师生活动:通过学生思考、交流,得出:
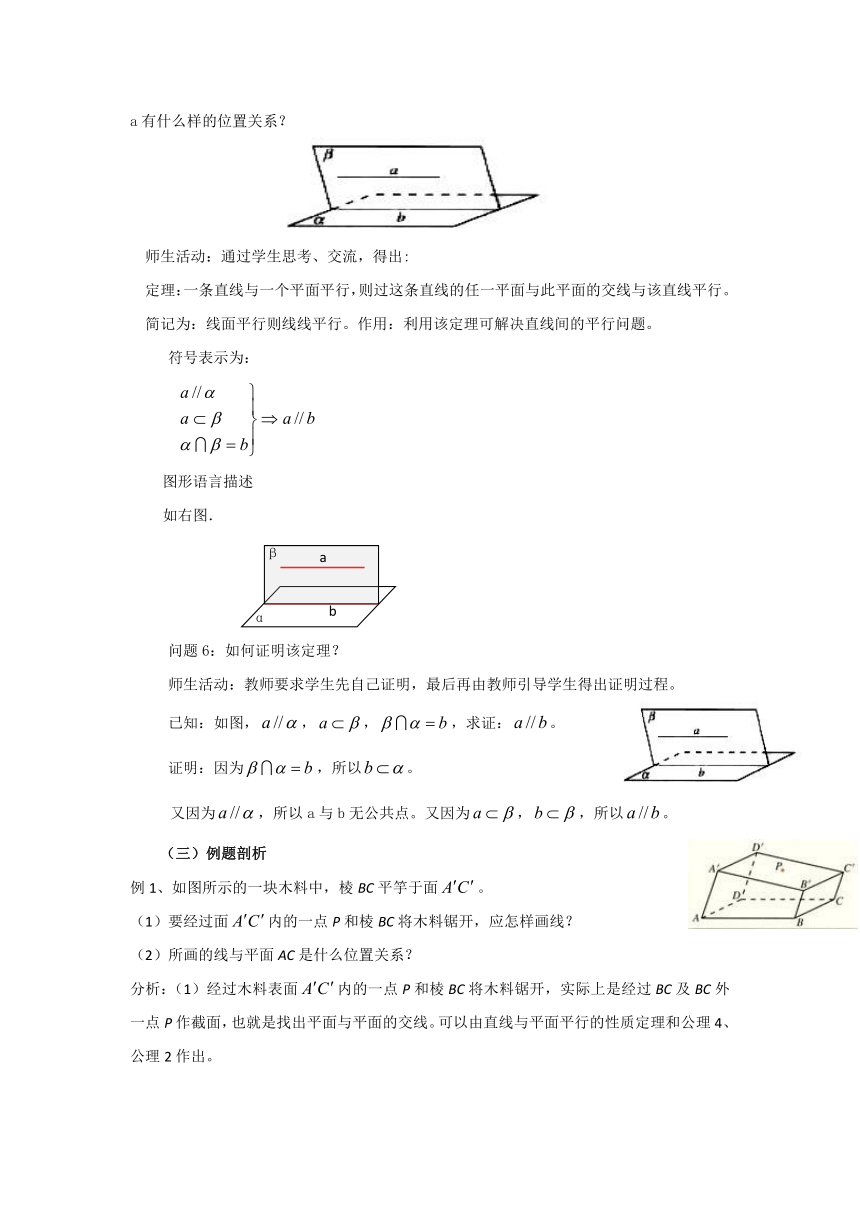
定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
简记为:线面平行则线线平行。作用:利用该定理可解决直线间的平行问题。
符号表示为:
图形语言描述
如右图.
问题6:如何证明该定理?
师生活动:教师要求学生先自己证明,最后再由教师引导学生得出证明过程。
已知:如图,,,,求证:。
证明:因为,所以。
又因为,所以a与b无公共点。又因为,,所以。
(三)例题剖析
例1、如图所示的一块木料中,棱BC平竽于面。
(1)要经过面内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线与平面AC是什么位置关系?
分析:(1)经过木料表面内的一点P和棱BC将木料锯开,实际上是经过BC及BC外一点P作截面,也就是找出平面与平面的交线。可以由直线与平面平行的性质定理和公理4、公理2作出。
(2)由于所作的直线EF平行于BC,所以所画的线EF与平面AC平行,而BE、CF则 与平面AC相交。
例2、已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面。
已知:,求证:。
证明:过直线a作平面β交平面α于直线c,因为,
所以a // c,因为a // b,所以b // c,又因为,所以。
说明:线线平行线面平行,转化是立体几何的一种重要的思想方法。
变式:求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行。
已知:,
求证:a // l。
分析:利用线面平行的性质定理。
证明:过a作平面交于b,因为,所以a // b,
过a作平面交平面于c,因为,所以a // c,所以b // c。[来源:Z|xx|k.Com]
又因为且,所以,[来源:学科网]
由于平面过b交于l,所以b // l,又a // b,所以a // l。
(四)课堂练习
1、填空:
(1)若两直线a、b异面,且a // α ,则b与α的位置关系可能是 。
(2)若两直线a、b相交,且a // α ,则b与α的位置关系可能是 。
2、长方体ABCD—A1B1C1D1中,点(异于B、B1),,
,求证:MN // 平面ABCD。
(五)归纳小结
证明线面平行的转化思想:
要证a // α ,通过构造过直线a的平面β与平面α相交于直线b,只要证明a // b即可。
线线平行线面平行面面平行((1)平行公理;(2)三角形中位线;(3)平行线分线段成比例;(4)相似三角形对应边成比例;(5)平行四边形对边平行。)[来源:学科网ZXXK]
(六)布置作业:(七)教学反思:
b
α
β
a
一、教学目标:
1、知识与技能:掌握直线与平面平行的性质定理及其应用。
2、过程与方法:学生通过观察与类比,借助实物模型理解性质及应用。
3、情感态度与价值观:进一步提高学生空间想象能力、思维能力;体会类比的作用;渗透等价转化的思想。
二、教学重、难点:
重点:直线与平面平行的性质定理的理解。[来源:学科网]
难点:直线与平面平行的性质定理的证明及正确运用。
三、学法指导:学生借助实物,通过类比、交流等,得出性质及基本应用。
四、教学过程:
(一)复习回顾
复习:(1)直线与平面平行的判定定理:。
(2)平面与平面平行的判定定理:
师生活动:教师提问,首先叫一个同学来回顾,然后让其他同学来补充完善。
答案:(1)不在平面内的一条直线与平面内的一条直线平行,则这条直线与这个平面行
(2)一个平面内的两条相交直线分别与另一个平面平行,则这两个平面平行
本质:线线平行推出线面平行,由线面平行可推出面面平行
(二)研探新知
问题1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?
师生活动:教师提问,学生思考回答。平行、异面
问题2:若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?
师生活动:教师提问,学生思考回答。无数条,平行
问题3:如何在平面α找到这些与直线a平行的直线?
师生活动:教师提问,学生思考回答。过直线a作平面
问题4:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?
师生活动:教师提问,学生思考回答。平行或相交
问题5:直线a与平面平行,过直线a的某一平面,若与平面相交,则交线与直线a有什么样的位置关系?
师生活动:通过学生思考、交流,得出:
定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
简记为:线面平行则线线平行。作用:利用该定理可解决直线间的平行问题。
符号表示为:
图形语言描述
如右图.
问题6:如何证明该定理?
师生活动:教师要求学生先自己证明,最后再由教师引导学生得出证明过程。
已知:如图,,,,求证:。
证明:因为,所以。
又因为,所以a与b无公共点。又因为,,所以。
(三)例题剖析
例1、如图所示的一块木料中,棱BC平竽于面。
(1)要经过面内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线与平面AC是什么位置关系?
分析:(1)经过木料表面内的一点P和棱BC将木料锯开,实际上是经过BC及BC外一点P作截面,也就是找出平面与平面的交线。可以由直线与平面平行的性质定理和公理4、公理2作出。
(2)由于所作的直线EF平行于BC,所以所画的线EF与平面AC平行,而BE、CF则 与平面AC相交。
例2、已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面。
已知:,求证:。
证明:过直线a作平面β交平面α于直线c,因为,
所以a // c,因为a // b,所以b // c,又因为,所以。
说明:线线平行线面平行,转化是立体几何的一种重要的思想方法。
变式:求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行。
已知:,
求证:a // l。
分析:利用线面平行的性质定理。
证明:过a作平面交于b,因为,所以a // b,
过a作平面交平面于c,因为,所以a // c,所以b // c。[来源:Z|xx|k.Com]
又因为且,所以,[来源:学科网]
由于平面过b交于l,所以b // l,又a // b,所以a // l。
(四)课堂练习
1、填空:
(1)若两直线a、b异面,且a // α ,则b与α的位置关系可能是 。
(2)若两直线a、b相交,且a // α ,则b与α的位置关系可能是 。
2、长方体ABCD—A1B1C1D1中,点(异于B、B1),,
,求证:MN // 平面ABCD。
(五)归纳小结
证明线面平行的转化思想:
要证a // α ,通过构造过直线a的平面β与平面α相交于直线b,只要证明a // b即可。
线线平行线面平行面面平行((1)平行公理;(2)三角形中位线;(3)平行线分线段成比例;(4)相似三角形对应边成比例;(5)平行四边形对边平行。)[来源:学科网ZXXK]
(六)布置作业:(七)教学反思:
b
α
β
a
