人教高中数学选修2-3:1.3.2二项式系数的性质-课件(共32张PPT)
文档属性
| 名称 | 人教高中数学选修2-3:1.3.2二项式系数的性质-课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 11:27:16 | ||
图片预览








文档简介
(共32张PPT)
复习回顾:
二项式定理及展开式:
1
3
二项式系数的性质
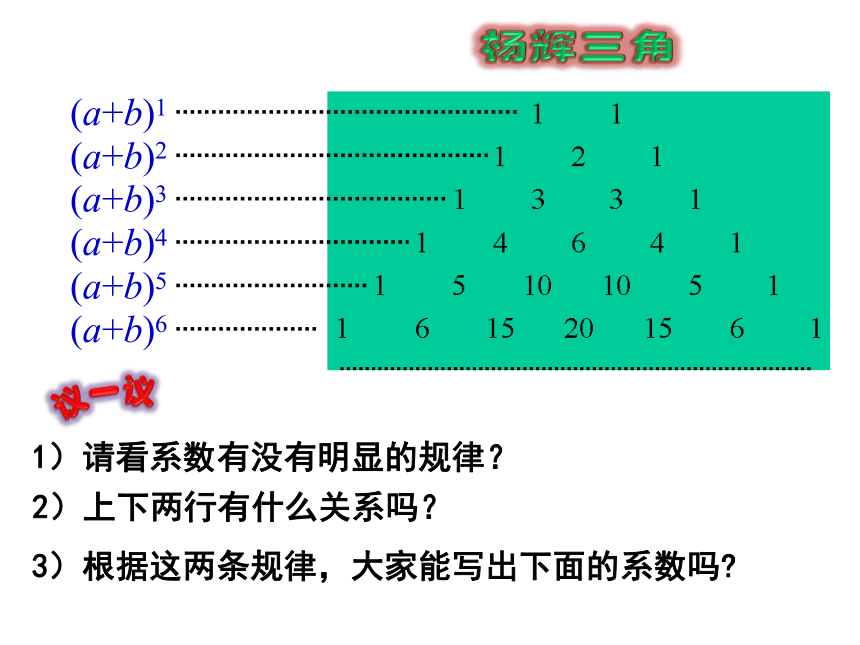
二项式系数表
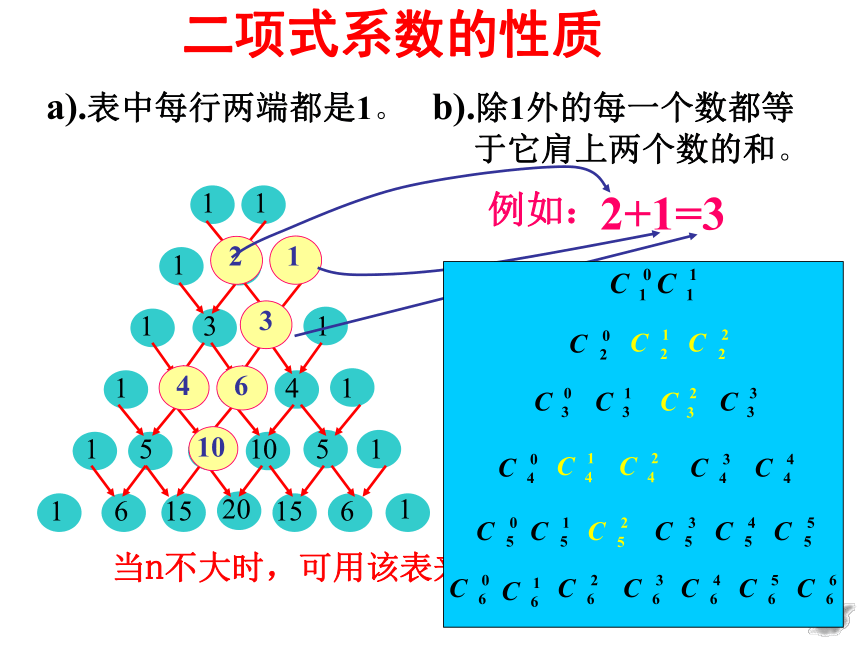
a).表中每行两端都是1。
b).除1外的每一个数都等
于它肩上两个数的和。
4+6=10
当n不大时,可用该表来求二项式系数。
二项式系数的性质
《详解九章算法》记载的表
杨辉 三角
杨辉
以上二项式系数表,早在我 国南宋数学家杨辉1261年所著的《详解九章算法》一书里就已经出现了,这个表称为杨辉三角。在《详解九章算法》一书里,还说明了表里“一”以外的每一个数都等于它肩上两个数的和,杨辉指出这个方法出于《释锁》算书,且我国北宋数学家贾宪(约公元11世纪)已经用过它。这表明我国发现这个表不晚于11世纪。在欧洲,这个表被认为是法国数学家帕斯卡(1623-1662)首先发现的,他们把这个表叫做帕斯卡三角。这就是说,杨辉三角的发现要比欧洲早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的。
二项式系数的性质
对称
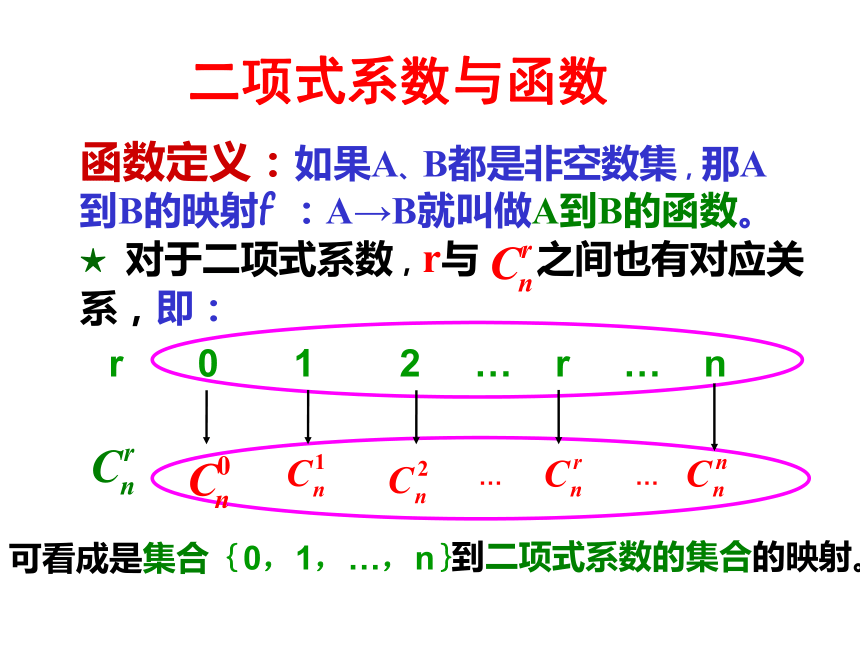
函数定义:如果A、B都是非空数集,那A到B的映射f :A→B就叫做A到B的函数。
可看成是集合{0,1,…,n}
到二项式系数的集合
的映射。
…
二项式系数与函数
…
从映射、函数的观点看,二项式系数可以看作是一个定义域为 {0,1,2,…,n}的函数当自变量从小到大依次取值时对应的一列函数值。
即:r是自变量,
二项式系数是函数值,
组合数公式就是相应函数的解析式。
1
2
3
二
项
式
二项式系数与函数
①当n=6时,二项式系数 (0≤r≤6)用图象表示:
1
3
……
n
…
1
2
3
2
2n
①与首末两端“等距离”
的两个二项式系数相等
1:对称性
2:增减性与最大值
①先增后减
②关于r= 3对称
②0~6,共7项,r=3时取得最大值
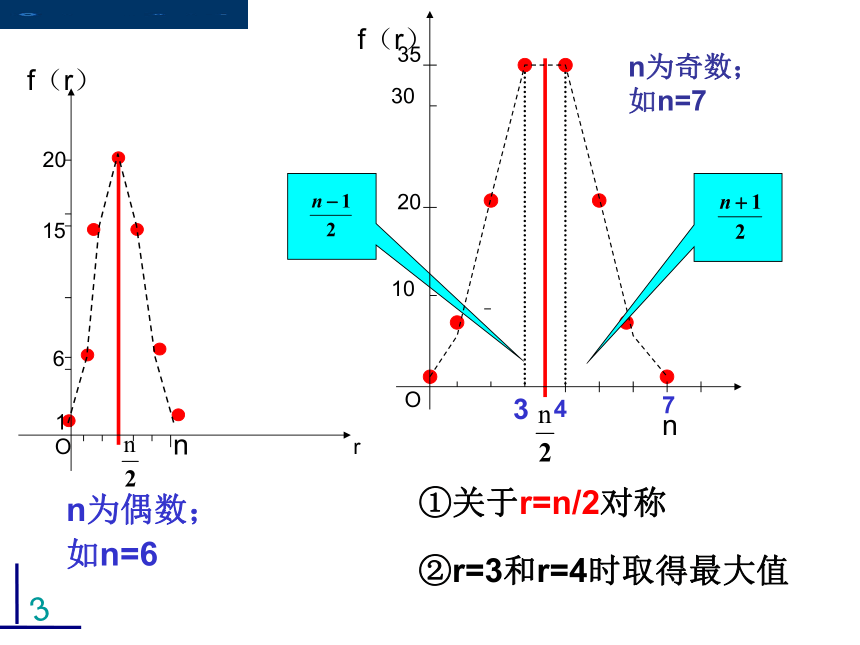
f(r)
n为奇数;
如n=7
3
n为偶数;
如n=6
①关于r=n/2对称
②r=3和r=4时取得最大值
二项式系数的性质
与首末两端“等距离”的两个二项式系数相等
性质1:对称性
性质2:增减性与最大值
先增后减
因而
2.增减性与最大值
且奇数项的二项式系数和等于偶数的二项式系数和
性质3:各二项式系数的和
二项式系数的性质
2n
令x=1:
令x=-1:
0
回顾例题
例1、证明(a+b)n 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。
所以(a+b)n 的展开式中,奇数项的二项式系数的和等于偶
数项的二项式系数的和。
变式练习1:
-2
-1094
1093
(1-2x)15的展开式中各项系数和是_____
(1-2x)15的展开式中所有二项式系数和是_____
变式练习2:
37
解:
拔高练习:
拔高练习:
证明略
例5.若 的展开式中,所有奇数项
的系数之和为1024,求它的中间项.
解:∵展开式中各项的二项式系数与该项的
的系数相等
∴由已知可得:2n-1=1024
解得 n=11,∴有两个中间项分别为
1
2
3
……
n
…
求解二项式系数和时,灵活运用赋值法可以使问题简单化。通常选取赋值时取-1,1,0。
例题讲解
例题讲解
练习
1、已知: 的展开式中所有二项系数和为128,则展开式中二项系数是最大的项
提高:
1、求 的展开式整理过后的常数项是多少?
2、求多项式(3x4-x3+2x2-3)8·(3x-5)4·(7x4-4x-2)6展开式各项系数的和.
解:设f( x )= (3x4-x3+2x2-3)8·(3x-5)4·(7x4-4x-2)6
= a0+a1x+a2x2+a3x3+……+a60x60.
所要求的各项系数的和就是a0+a1+a2+……+a60.
又将x=1代入得 f(1)= a0+a1+a2+……+a60
=(3-1+2-3)8(3-5)4(7-4-2)6=16.
∴ 各项系数的和为16.
1、在(a+b)20展开式中,与第五项二项式系数相同的项是( ).
C
课堂练习:
A.第6项 B.第7项 C.第6项和第7项 D.第5项和第7项
C
A.第15项 B.第16项 C.第17项 D.第18项
2、在(a+b)11展开式中,二项式系数最大的项( ).
18
小结:
(3) 数学方法 : 赋值法
(1)二项式系数的三个性质
课后作业
1. 已知(3-2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则
(1)a0+a2+a4的值为________;
(2)|a1|+|a2|+|a3|+|a4|+|a5|=_________.
(55+1)/2
2882
2. 2C02n+C12n+2C22n+C32n+…+2C2k2n+C2k+12n+…+C2n-12n
+2C2n2n=________.
3·22n-1
复习回顾:
二项式定理及展开式:
1
3
二项式系数的性质
二项式系数表
a).表中每行两端都是1。
b).除1外的每一个数都等
于它肩上两个数的和。
4+6=10
当n不大时,可用该表来求二项式系数。
二项式系数的性质
《详解九章算法》记载的表
杨辉 三角
杨辉
以上二项式系数表,早在我 国南宋数学家杨辉1261年所著的《详解九章算法》一书里就已经出现了,这个表称为杨辉三角。在《详解九章算法》一书里,还说明了表里“一”以外的每一个数都等于它肩上两个数的和,杨辉指出这个方法出于《释锁》算书,且我国北宋数学家贾宪(约公元11世纪)已经用过它。这表明我国发现这个表不晚于11世纪。在欧洲,这个表被认为是法国数学家帕斯卡(1623-1662)首先发现的,他们把这个表叫做帕斯卡三角。这就是说,杨辉三角的发现要比欧洲早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的。
二项式系数的性质
对称
函数定义:如果A、B都是非空数集,那A到B的映射f :A→B就叫做A到B的函数。
可看成是集合{0,1,…,n}
到二项式系数的集合
的映射。
…
二项式系数与函数
…
从映射、函数的观点看,二项式系数可以看作是一个定义域为 {0,1,2,…,n}的函数当自变量从小到大依次取值时对应的一列函数值。
即:r是自变量,
二项式系数是函数值,
组合数公式就是相应函数的解析式。
1
2
3
二
项
式
二项式系数与函数
①当n=6时,二项式系数 (0≤r≤6)用图象表示:
1
3
……
n
…
1
2
3
2
2n
①与首末两端“等距离”
的两个二项式系数相等
1:对称性
2:增减性与最大值
①先增后减
②关于r= 3对称
②0~6,共7项,r=3时取得最大值
f(r)
n为奇数;
如n=7
3
n为偶数;
如n=6
①关于r=n/2对称
②r=3和r=4时取得最大值
二项式系数的性质
与首末两端“等距离”的两个二项式系数相等
性质1:对称性
性质2:增减性与最大值
先增后减
因而
2.增减性与最大值
且奇数项的二项式系数和等于偶数的二项式系数和
性质3:各二项式系数的和
二项式系数的性质
2n
令x=1:
令x=-1:
0
回顾例题
例1、证明(a+b)n 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。
所以(a+b)n 的展开式中,奇数项的二项式系数的和等于偶
数项的二项式系数的和。
变式练习1:
-2
-1094
1093
(1-2x)15的展开式中各项系数和是_____
(1-2x)15的展开式中所有二项式系数和是_____
变式练习2:
37
解:
拔高练习:
拔高练习:
证明略
例5.若 的展开式中,所有奇数项
的系数之和为1024,求它的中间项.
解:∵展开式中各项的二项式系数与该项的
的系数相等
∴由已知可得:2n-1=1024
解得 n=11,∴有两个中间项分别为
1
2
3
……
n
…
求解二项式系数和时,灵活运用赋值法可以使问题简单化。通常选取赋值时取-1,1,0。
例题讲解
例题讲解
练习
1、已知: 的展开式中所有二项系数和为128,则展开式中二项系数是最大的项
提高:
1、求 的展开式整理过后的常数项是多少?
2、求多项式(3x4-x3+2x2-3)8·(3x-5)4·(7x4-4x-2)6展开式各项系数的和.
解:设f( x )= (3x4-x3+2x2-3)8·(3x-5)4·(7x4-4x-2)6
= a0+a1x+a2x2+a3x3+……+a60x60.
所要求的各项系数的和就是a0+a1+a2+……+a60.
又将x=1代入得 f(1)= a0+a1+a2+……+a60
=(3-1+2-3)8(3-5)4(7-4-2)6=16.
∴ 各项系数的和为16.
1、在(a+b)20展开式中,与第五项二项式系数相同的项是( ).
C
课堂练习:
A.第6项 B.第7项 C.第6项和第7项 D.第5项和第7项
C
A.第15项 B.第16项 C.第17项 D.第18项
2、在(a+b)11展开式中,二项式系数最大的项( ).
18
小结:
(3) 数学方法 : 赋值法
(1)二项式系数的三个性质
课后作业
1. 已知(3-2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则
(1)a0+a2+a4的值为________;
(2)|a1|+|a2|+|a3|+|a4|+|a5|=_________.
(55+1)/2
2882
2. 2C02n+C12n+2C22n+C32n+…+2C2k2n+C2k+12n+…+C2n-12n
+2C2n2n=________.
3·22n-1
