人教A版高中数学必修一第二章第一节指数函数课件(共16张PPT)
文档属性
| 名称 | 人教A版高中数学必修一第二章第一节指数函数课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 14:52:47 | ||
图片预览





文档简介
(共16张PPT)
第二章
基本初等函数
2.1.2
指数函数图像及其性质
合肥理工学校 高一数学组
1
学习目标
2
3
指数函数的概念
指数函数的图像
指数函数的性质
指数函数图像及其性质
课程导入
破产的国王
从前有个人发明了国际象棋。国王很高兴,准备赏赐他。那个人说。我不要金银,只要大米,国王问他你要多少米?那个人说:国际象棋有64个格,第一个格放2粒米,第二个格子有4粒米,第三个格子放8粒米,以此类推,我只要第64格大米的数量。
可是后来,国王破产了,你知道为什么吗?
情境一
课程导入
情境一
每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子
陛下,赏小人几粒麦子就行。
我很喜欢你的发明,你要什么赏赐?
情境一
课程导入
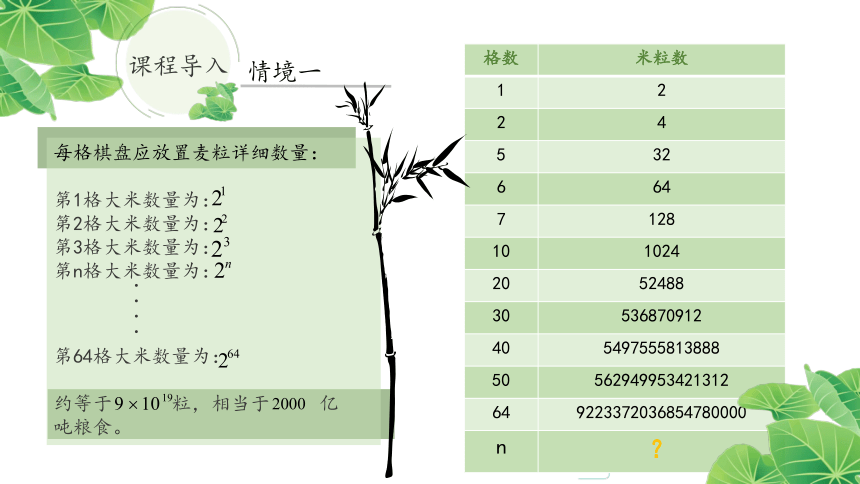
每格棋盘应放置麦粒详细数量:
第1格大米数量为:
第2格大米数量为:
第3格大米数量为:
第n格大米数量为:
·
·
·
·
第64格大米数量为:
约等于 粒,相当于 亿 吨粮食。
格数 米粒数
1 2
2 4
5 32
6 64
7 128
10 1024
20 52488
30 536870912
40 5497555813888
50 562949953421312
64 9223372036854780000
n ?
情境二
课程导入
有一张纸,假设它的长度是1
对折以后,它的长度是:
再对折以后它的长度是:
·
·
·
对折n次以后它的长度是:
思考
情境一所得到的函数为:
情境二所得到的函数为:
以上函数有什么共同特征?
引入目的
共同特征为:底数不变,指数可变,即底数为常数,指数为自变量
指数函数的概念
概念
一般地,函数y=ax (a>0,且a≠1)叫做指数函数(exponential function),其中x是自变量,函数的定义域是R。
指数函数的底数要求
概念
讨论:y=ax (a>0且a≠1) ,当x取全体实数时,对y=ax 中的底 数为什么要求a>0且a≠1?
指数函数的底数要求
概念
当a>0时, ax有意义
当a=1时, ,无研究价值
当a=0时,若x>0 ,则 ,无研究价值
若x≤0 ,则 ,如 ,无意义
当a<0时,ax不一定有意义,如 无意义
为了便于研究,我们规定:a>0且a≠1。
指数函数的特征
概念
底数为常数(大于0且不等于1)
自变量系数为1
函数系数为1
y=1 · a1·x
下列哪些函数是指数函数
√
×
×
×
×
指数函数的图像
图像
y
x
0
y= 2x
y = x
8
7
6
5
4
3
2
1
-3 -2 -1
-1
-2
-3
y = 2x
x -1 0 1 2 3
y
x -3 -2 -1 0 1
y
y = x
图像关于y轴对称
8
4
2
1
0.5
8
4
2
1
0.5
x
y
o
1
0
x
y
o
1
a>1
2
2
a>1
0图 象
性 质
1.定义域:
2. 值域:
y=ax
y=ax
单调性:
单调性:
对称性:
3. 过定点:
评
性质
指数函数的性质
课堂检测
1、下列函数中,哪些是指数函数?
⑴ y=10x; ⑵ y=10x+1;
⑶ y=10x+1; ⑷ y=2·10x;
⑸ y=(-10) x;
2、用“>”或“<”填空:
√
×
×
×
×
<
<
>
<
⑴
⑵
⑶
⑷
指数鸡汤
思考
每天进步一点点
坚持带来大改变
谢谢观赏
第二章
基本初等函数
2.1.2
指数函数图像及其性质
合肥理工学校 高一数学组
1
学习目标
2
3
指数函数的概念
指数函数的图像
指数函数的性质
指数函数图像及其性质
课程导入
破产的国王
从前有个人发明了国际象棋。国王很高兴,准备赏赐他。那个人说。我不要金银,只要大米,国王问他你要多少米?那个人说:国际象棋有64个格,第一个格放2粒米,第二个格子有4粒米,第三个格子放8粒米,以此类推,我只要第64格大米的数量。
可是后来,国王破产了,你知道为什么吗?
情境一
课程导入
情境一
每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64个格子
陛下,赏小人几粒麦子就行。
我很喜欢你的发明,你要什么赏赐?
情境一
课程导入
每格棋盘应放置麦粒详细数量:
第1格大米数量为:
第2格大米数量为:
第3格大米数量为:
第n格大米数量为:
·
·
·
·
第64格大米数量为:
约等于 粒,相当于 亿 吨粮食。
格数 米粒数
1 2
2 4
5 32
6 64
7 128
10 1024
20 52488
30 536870912
40 5497555813888
50 562949953421312
64 9223372036854780000
n ?
情境二
课程导入
有一张纸,假设它的长度是1
对折以后,它的长度是:
再对折以后它的长度是:
·
·
·
对折n次以后它的长度是:
思考
情境一所得到的函数为:
情境二所得到的函数为:
以上函数有什么共同特征?
引入目的
共同特征为:底数不变,指数可变,即底数为常数,指数为自变量
指数函数的概念
概念
一般地,函数y=ax (a>0,且a≠1)叫做指数函数(exponential function),其中x是自变量,函数的定义域是R。
指数函数的底数要求
概念
讨论:y=ax (a>0且a≠1) ,当x取全体实数时,对y=ax 中的底 数为什么要求a>0且a≠1?
指数函数的底数要求
概念
当a>0时, ax有意义
当a=1时, ,无研究价值
当a=0时,若x>0 ,则 ,无研究价值
若x≤0 ,则 ,如 ,无意义
当a<0时,ax不一定有意义,如 无意义
为了便于研究,我们规定:a>0且a≠1。
指数函数的特征
概念
底数为常数(大于0且不等于1)
自变量系数为1
函数系数为1
y=1 · a1·x
下列哪些函数是指数函数
√
×
×
×
×
指数函数的图像
图像
y
x
0
y= 2x
y = x
8
7
6
5
4
3
2
1
-3 -2 -1
-1
-2
-3
y = 2x
x -1 0 1 2 3
y
x -3 -2 -1 0 1
y
y = x
图像关于y轴对称
8
4
2
1
0.5
8
4
2
1
0.5
x
y
o
1
0
x
y
o
1
a>1
2
2
a>1
0
性 质
1.定义域:
2. 值域:
y=ax
y=ax
单调性:
单调性:
对称性:
3. 过定点:
评
性质
指数函数的性质
课堂检测
1、下列函数中,哪些是指数函数?
⑴ y=10x; ⑵ y=10x+1;
⑶ y=10x+1; ⑷ y=2·10x;
⑸ y=(-10) x;
2、用“>”或“<”填空:
√
×
×
×
×
<
<
>
<
⑴
⑵
⑶
⑷
指数鸡汤
思考
每天进步一点点
坚持带来大改变
谢谢观赏
