北京版八年级下册数学15.1 多边形内角和与外角和课件 (共87张PPT)
文档属性
| 名称 | 北京版八年级下册数学15.1 多边形内角和与外角和课件 (共87张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
图片预览









文档简介
(共87张PPT)
初二年级 数学
多边形内角和与外角和
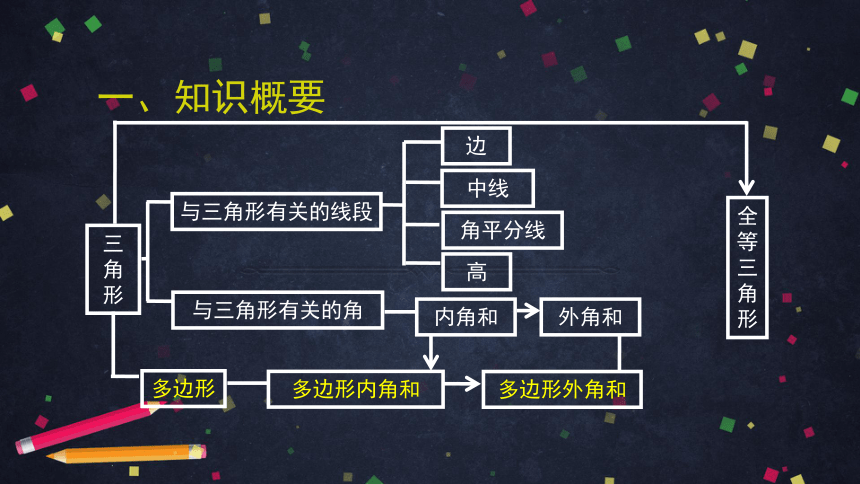
一、知识概要
二、关键问题
三、典型例题
一、知识概要
二、关键问题
三、典型例题
边
高
中线
角平分线
内角和
外角和
三
角
形
全
等
三
角
形
与三角形有关的线段
与三角形有关的角
多边形
多边形内角和
多边形外角和
一、知识概要
一、知识概要
二、关键问题
三、典型例题
二、关键问题
2.多边形的内角和是多少?为什么?
3.多边形的外角和是多少?为什么?
1.明确研究的对象,什么叫多边形?
1.明确研究的对象,什么叫多边形?
二、关键问题
二、关键问题
1.明确研究的对象,什么叫多边形?
由不在同一条直线上的三条线段首尾顺次相接组成的图形叫做三角形.
二、关键问题
1.明确研究的对象,什么叫多边形?
由不在同一条直线上的三条线段首尾顺次相接组成的图形叫做三角形.
二、关键问题
1.明确研究的对象,什么叫多边形?
二、关键问题
由n条线段首尾顺次相接组成的平面图形
称为n边形,又称为多边形.
1.明确研究的对象,什么叫多边形?
如图,把多边形的任意一边向两个方向延长,如果其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形,现在我们只研究凸多边形.
二、关键问题
二、关键问题
2.多边形的内角和是多少?为什么?
二、关键问题
2.多边形的内角和是多少?为什么?
如图,四边形ABCD的
四条边分别是AB, BC,CD ,DA ,
四个顶点分别是点A ,B ,C ,D ,
四个内角(简称角)分别是
∠A ,∠B ,∠C ,∠D.
如图,四边形ABCD的
四条边分别是AB, BC,CD ,DA ,
四个顶点分别是点A ,B ,C ,D ,
四个内角(简称角)分别是
∠A ,∠B ,∠C ,∠D.
二、关键问题
2.多边形的内角和是多少?为什么?
四边形的内角和=∠A+∠B+∠C+∠D.
2.多边形的内角和是多少?为什么?
二、关键问题
二、关键问题
2.多边形的内角和是多少?为什么?
2.多边形的内角和是多少?为什么?
四边形内角和
=∠A+∠B+∠C+∠D
二、关键问题
二、关键问题
2.多边形的内角和是多少?为什么?
连接多边形不相邻的两个顶点的
线段叫做多边形的对角线.
二、关键问题
2.多边形的内角和是多少?为什么?
四边形内角和
=△ABC的内角和+△ACD的内角和
=180°+ 180°
=360°.
二、关键问题
2.多边形的内角和是多少?为什么?
四边形内角和
E
=△ABE的内角和+△ADE的内角和
+△BCE的内角和-180°
=180°+ 180°+ 180° -180°
=360°.
二、关键问题
2.多边形的内角和是多少?为什么?
四边形内角和
=△ABE的内角和+△BCE的内角和
+△CDE的内角和+△ADE的内角和-360°
=180°+ 180°+ 180° +180°- 360°
=360°.
E
E
E
二、关键问题
五边形内角和
=180°×3
=540°.
2.多边形的内角和是多少?为什么?
二、关键问题
六边形内角和
=180°×4
=720°.
2.多边形的内角和是多少?为什么?
多边形
四边形
五边形
六边形
…
n边形
…
…
…
图形
分成三角
形的个数
2
3
4
(4-2)×180°
(5-2)×180°
(6-2)×180°
(n-2)×180°
(n-2)
内角和
小结
研究数学问题时,
从简单到复杂,
从具体到抽象,
从特殊到一般.
3.多边形的外角和是多少?为什么?
如图,四边形ABCD的∠DCE和∠BCF
都是与∠DCB相邻的外角,两者互为
对顶角.
二、关键问题
3.多边形的外角和是多少?为什么?
如图,四边形ABCD的∠DCE和∠BCF
都是与∠DCB相邻的外角,两者互为
对顶角.在多边形的每个顶点处取
多边形的一个外角,它们的和叫做
多边形的外角和.
二、关键问题
二、关键问题
3.多边形的外角和是多少?为什么?
四边形外角和
=∠1+∠2+∠3+∠4
二、关键问题
3.多边形的外角和是多少?为什么?
二、关键问题
= (180°-∠BAD )+ (180°-∠ABC )
+ (180°-∠BCD )+ (180°-∠CDA )
四边形外角和
=∠1+∠2+∠3+∠4
3.多边形的外角和是多少?为什么?
二、关键问题
= (180°-∠BAD )+ (180°-∠ABC )
+ (180°-∠BCD )+ (180°-∠CDA )
四边形外角和
=∠1+∠2+∠3+∠4
3.多边形的外角和是多少?为什么?
=720°- (∠BAD +∠ABC+∠BCD + ∠CDA )
二、关键问题
= (180°-∠BAD )+ (180°-∠ABC )
+ (180°-∠BCD )+ (180°-∠CDA )
四边形外角和
=∠1+∠2+∠3+∠4
3.多边形的外角和是多少?为什么?
=720°- (∠BAD +∠ABC+∠BCD + ∠CDA )
=360°.
二、关键问题
= (180°-∠BAD )+ (180°-∠ABC )
+ (180°-∠BCD )+ (180°-∠CDA )
四边形外角和
=∠1+∠2+∠3+∠4
3.多边形的外角和是多少?为什么?
=720°- (∠BAD +∠ABC+∠BCD + ∠CDA )
=360°.
四边形的外角和是360°.
3.多边形的外角和是多少?为什么?
二、关键问题
3.多边形的外角和是多少?为什么?
二、关键问题
3.多边形的外角和是多少?为什么?
二、关键问题
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
每个顶点处有一个外角与它相邻的内角组成一个平角,
共5×180°,
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
内角和为(5-2)×180°,
每个顶点处有一个外角与它相邻的内角组成一个平角,
共5×180°,
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
做差,
内角和为(5-2)×180°,
每个顶点处有一个外角与它相邻的内角组成一个平角,
共5×180°,
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
五边形的外角和是360°.
做差,
内角和为(5-2)×180°,
每个顶点处有一个外角与它相邻的内角组成一个平角,
共5×180°,
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
证明:n边形有n个顶点,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
每个顶点处一个外角与相邻内角组成一个平角,
共n×180°,
证明:n边形有n个顶点,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
内角和为(n-2)×180°,
每个顶点处一个外角与相邻内角组成一个平角,
共n×180°,
证明:n边形有n个顶点,
每个顶点处一个外角与相邻内角组成一个平角,
共n×180°,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
做差,
内角和为(n-2)×180°,
证明:n边形有n个顶点,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
多边形的外角和是360°.
做差,
内角和为(n-2)×180°,
每个顶点处一个外角与相邻内角组成一个平角,
共n×180°,
证明:n边形有n个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
n边形的内角和为(n-2)·180°.
多边形的外角和都是360°.
多边形内角和与外角和
一、知识概要
二、关键问题
三、典型例题
例 求出图中x的值.
三、典型例题
解:
(1)
(2)
例 求出图中x的值.
三、典型例题
解:
(1)
60°+4x°= (5-2)×180°
(1)
(2)
例 求出图中x的值.
三、典型例题
解:
(1)
60°+4x°= (5-2)×180°
x = 120.
(1)
(2)
例 求出图中x的值.
三、典型例题
解:
(1)
(2)
60°+4x°= (5-2)×180°
x = 120.
3x°+3x°+4x°+2x°= 360°
(1)
(2)
例 求出图中x的值.
三、典型例题
解:
(1)
(2)
60°+4x°= (5-2)×180°
x = 120.
3x°+3x°+4x°+2x°= 360°
x= 30.
(1)
(2)
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
三、典型例题
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
三、典型例题
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
(n-2)·180°
n
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
(n-2)·180°
n
144°.
=
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
(n-2)·180°
n
144°.
=
解得 n=10.
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
(n-2)·180°
n
144°.
=
答:这个多边形是十边形.
解得 n=10.
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
三、典型例题
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法2:
三、典型例题
每个外角都为36°,
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法2:
三、典型例题
360÷36=10.
每个外角都为36°,
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法2:
三、典型例题
360÷36=10.
答:这个多边形是十边形.
每个外角都为36°,
探求问题的本质,
寻找事物的规律,
用最简单的形式表达,
是数学家的追求.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
三、典型例题
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
(n-2)·180°
n
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
3
2
(n-2)·180°
n
·
=
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
3
2
(n-2)·180°
n
·
=
解得 n=5.
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
3
2
(n-2)·180°
n
·
=
解得 n=5.
答:这个多边形是五边形.
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
三、典型例题
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
(180-y)
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
y
(180-y)
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
3
2
·
=
.
y
(180-y)
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
3
2
·
=
解得
y
y =72.
(180-y)
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
3
2
·
=
解得
y
y =72.
(180-y)
360÷72=5.
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
3
2
·
=
解得
答:这个多边形是五边形.
y
y =72.
(180-y)
360÷72=5.
.
边
高
中线
角平分线
内角和
外角和
三
角
形
全
等
三
角
形
与三角形有关的线段
与三角形有关的角
多边形
多边形内角和
多边形外角和
(n-2) · 180°(n为边数)
360°
三角形具有稳定性,四边形具有不稳定性.
作业
1.计算下列多边形的内角和:
(1)五边形;(2)八边形;(3)十边形.
2.(1)一个多边形的内角和是外角和的一半,它是几边形?(2)一个多边形的内角和是外角和的2倍,它是几边形?
3.如图,五边形ABCDE的内角都相等,且∠1 = ∠2,∠3 = ∠4,求x的值.
作业
初二年级 数学
多边形内角和与外角和
一、知识概要
二、关键问题
三、典型例题
一、知识概要
二、关键问题
三、典型例题
边
高
中线
角平分线
内角和
外角和
三
角
形
全
等
三
角
形
与三角形有关的线段
与三角形有关的角
多边形
多边形内角和
多边形外角和
一、知识概要
一、知识概要
二、关键问题
三、典型例题
二、关键问题
2.多边形的内角和是多少?为什么?
3.多边形的外角和是多少?为什么?
1.明确研究的对象,什么叫多边形?
1.明确研究的对象,什么叫多边形?
二、关键问题
二、关键问题
1.明确研究的对象,什么叫多边形?
由不在同一条直线上的三条线段首尾顺次相接组成的图形叫做三角形.
二、关键问题
1.明确研究的对象,什么叫多边形?
由不在同一条直线上的三条线段首尾顺次相接组成的图形叫做三角形.
二、关键问题
1.明确研究的对象,什么叫多边形?
二、关键问题
由n条线段首尾顺次相接组成的平面图形
称为n边形,又称为多边形.
1.明确研究的对象,什么叫多边形?
如图,把多边形的任意一边向两个方向延长,如果其他各边都在延长所得直线的同一旁,这样的多边形叫做凸多边形,现在我们只研究凸多边形.
二、关键问题
二、关键问题
2.多边形的内角和是多少?为什么?
二、关键问题
2.多边形的内角和是多少?为什么?
如图,四边形ABCD的
四条边分别是AB, BC,CD ,DA ,
四个顶点分别是点A ,B ,C ,D ,
四个内角(简称角)分别是
∠A ,∠B ,∠C ,∠D.
如图,四边形ABCD的
四条边分别是AB, BC,CD ,DA ,
四个顶点分别是点A ,B ,C ,D ,
四个内角(简称角)分别是
∠A ,∠B ,∠C ,∠D.
二、关键问题
2.多边形的内角和是多少?为什么?
四边形的内角和=∠A+∠B+∠C+∠D.
2.多边形的内角和是多少?为什么?
二、关键问题
二、关键问题
2.多边形的内角和是多少?为什么?
2.多边形的内角和是多少?为什么?
四边形内角和
=∠A+∠B+∠C+∠D
二、关键问题
二、关键问题
2.多边形的内角和是多少?为什么?
连接多边形不相邻的两个顶点的
线段叫做多边形的对角线.
二、关键问题
2.多边形的内角和是多少?为什么?
四边形内角和
=△ABC的内角和+△ACD的内角和
=180°+ 180°
=360°.
二、关键问题
2.多边形的内角和是多少?为什么?
四边形内角和
E
=△ABE的内角和+△ADE的内角和
+△BCE的内角和-180°
=180°+ 180°+ 180° -180°
=360°.
二、关键问题
2.多边形的内角和是多少?为什么?
四边形内角和
=△ABE的内角和+△BCE的内角和
+△CDE的内角和+△ADE的内角和-360°
=180°+ 180°+ 180° +180°- 360°
=360°.
E
E
E
二、关键问题
五边形内角和
=180°×3
=540°.
2.多边形的内角和是多少?为什么?
二、关键问题
六边形内角和
=180°×4
=720°.
2.多边形的内角和是多少?为什么?
多边形
四边形
五边形
六边形
…
n边形
…
…
…
图形
分成三角
形的个数
2
3
4
(4-2)×180°
(5-2)×180°
(6-2)×180°
(n-2)×180°
(n-2)
内角和
小结
研究数学问题时,
从简单到复杂,
从具体到抽象,
从特殊到一般.
3.多边形的外角和是多少?为什么?
如图,四边形ABCD的∠DCE和∠BCF
都是与∠DCB相邻的外角,两者互为
对顶角.
二、关键问题
3.多边形的外角和是多少?为什么?
如图,四边形ABCD的∠DCE和∠BCF
都是与∠DCB相邻的外角,两者互为
对顶角.在多边形的每个顶点处取
多边形的一个外角,它们的和叫做
多边形的外角和.
二、关键问题
二、关键问题
3.多边形的外角和是多少?为什么?
四边形外角和
=∠1+∠2+∠3+∠4
二、关键问题
3.多边形的外角和是多少?为什么?
二、关键问题
= (180°-∠BAD )+ (180°-∠ABC )
+ (180°-∠BCD )+ (180°-∠CDA )
四边形外角和
=∠1+∠2+∠3+∠4
3.多边形的外角和是多少?为什么?
二、关键问题
= (180°-∠BAD )+ (180°-∠ABC )
+ (180°-∠BCD )+ (180°-∠CDA )
四边形外角和
=∠1+∠2+∠3+∠4
3.多边形的外角和是多少?为什么?
=720°- (∠BAD +∠ABC+∠BCD + ∠CDA )
二、关键问题
= (180°-∠BAD )+ (180°-∠ABC )
+ (180°-∠BCD )+ (180°-∠CDA )
四边形外角和
=∠1+∠2+∠3+∠4
3.多边形的外角和是多少?为什么?
=720°- (∠BAD +∠ABC+∠BCD + ∠CDA )
=360°.
二、关键问题
= (180°-∠BAD )+ (180°-∠ABC )
+ (180°-∠BCD )+ (180°-∠CDA )
四边形外角和
=∠1+∠2+∠3+∠4
3.多边形的外角和是多少?为什么?
=720°- (∠BAD +∠ABC+∠BCD + ∠CDA )
=360°.
四边形的外角和是360°.
3.多边形的外角和是多少?为什么?
二、关键问题
3.多边形的外角和是多少?为什么?
二、关键问题
3.多边形的外角和是多少?为什么?
二、关键问题
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
每个顶点处有一个外角与它相邻的内角组成一个平角,
共5×180°,
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
内角和为(5-2)×180°,
每个顶点处有一个外角与它相邻的内角组成一个平角,
共5×180°,
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
做差,
内角和为(5-2)×180°,
每个顶点处有一个外角与它相邻的内角组成一个平角,
共5×180°,
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
五边形的外角和是360°.
做差,
内角和为(5-2)×180°,
每个顶点处有一个外角与它相邻的内角组成一个平角,
共5×180°,
分析:五边形有五个顶点,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
证明:n边形有n个顶点,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
每个顶点处一个外角与相邻内角组成一个平角,
共n×180°,
证明:n边形有n个顶点,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
内角和为(n-2)×180°,
每个顶点处一个外角与相邻内角组成一个平角,
共n×180°,
证明:n边形有n个顶点,
每个顶点处一个外角与相邻内角组成一个平角,
共n×180°,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
做差,
内角和为(n-2)×180°,
证明:n边形有n个顶点,
3.多边形的外角和是多少?为什么?
求证:多边形的外角和是360°.
二、关键问题
多边形的外角和是360°.
做差,
内角和为(n-2)×180°,
每个顶点处一个外角与相邻内角组成一个平角,
共n×180°,
证明:n边形有n个顶点,
3.多边形的外角和是多少?为什么?
二、关键问题
n边形的内角和为(n-2)·180°.
多边形的外角和都是360°.
多边形内角和与外角和
一、知识概要
二、关键问题
三、典型例题
例 求出图中x的值.
三、典型例题
解:
(1)
(2)
例 求出图中x的值.
三、典型例题
解:
(1)
60°+4x°= (5-2)×180°
(1)
(2)
例 求出图中x的值.
三、典型例题
解:
(1)
60°+4x°= (5-2)×180°
x = 120.
(1)
(2)
例 求出图中x的值.
三、典型例题
解:
(1)
(2)
60°+4x°= (5-2)×180°
x = 120.
3x°+3x°+4x°+2x°= 360°
(1)
(2)
例 求出图中x的值.
三、典型例题
解:
(1)
(2)
60°+4x°= (5-2)×180°
x = 120.
3x°+3x°+4x°+2x°= 360°
x= 30.
(1)
(2)
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
三、典型例题
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
三、典型例题
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
(n-2)·180°
n
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
(n-2)·180°
n
144°.
=
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
(n-2)·180°
n
144°.
=
解得 n=10.
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法1:设这个多边形的边数为n.
三、典型例题
(n-2)·180°
n
144°.
=
答:这个多边形是十边形.
解得 n=10.
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
三、典型例题
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法2:
三、典型例题
每个外角都为36°,
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法2:
三、典型例题
360÷36=10.
每个外角都为36°,
例 如果一个多边形的每个内角都为144°,
求这个多边形的边数.
解法2:
三、典型例题
360÷36=10.
答:这个多边形是十边形.
每个外角都为36°,
探求问题的本质,
寻找事物的规律,
用最简单的形式表达,
是数学家的追求.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
三、典型例题
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
(n-2)·180°
n
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
3
2
(n-2)·180°
n
·
=
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
3
2
(n-2)·180°
n
·
=
解得 n=5.
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的边数为n.
三、典型例题
360°
n
3
2
(n-2)·180°
n
·
=
解得 n=5.
答:这个多边形是五边形.
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
三、典型例题
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
(180-y)
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
y
(180-y)
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
3
2
·
=
.
y
(180-y)
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
3
2
·
=
解得
y
y =72.
(180-y)
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
3
2
·
=
解得
y
y =72.
(180-y)
360÷72=5.
.
例 已知一个多边形的每一个外角都相等,它的一个外角等于一个内角的三分之二,这个多边形是几边形?
解:设这个多边形的外角度数为y.
三、典型例题
3
2
·
=
解得
答:这个多边形是五边形.
y
y =72.
(180-y)
360÷72=5.
.
边
高
中线
角平分线
内角和
外角和
三
角
形
全
等
三
角
形
与三角形有关的线段
与三角形有关的角
多边形
多边形内角和
多边形外角和
(n-2) · 180°(n为边数)
360°
三角形具有稳定性,四边形具有不稳定性.
作业
1.计算下列多边形的内角和:
(1)五边形;(2)八边形;(3)十边形.
2.(1)一个多边形的内角和是外角和的一半,它是几边形?(2)一个多边形的内角和是外角和的2倍,它是几边形?
3.如图,五边形ABCDE的内角都相等,且∠1 = ∠2,∠3 = ∠4,求x的值.
作业
同课章节目录
