沪教版(上海)八年级下数学 22.3 特殊的平行四边 测试题(含答案)
文档属性
| 名称 | 沪教版(上海)八年级下数学 22.3 特殊的平行四边 测试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 133.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 14:54:26 | ||
图片预览


文档简介
22.3 特殊的平行四边 测试题
一.选择题
1.下列命题中不正确的是( ).
A.直角三角形斜边中线等于斜边的一半
B.矩形的对角线相等
C.矩形的对角线互相垂直
D.矩形是轴对称图形
2.若矩形对角线相交所成钝角为120°,短边长3.6,则对角线的长为( ).
A. 3.6 B. 7.2 C. 1.8 D. 14.4
3.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是( )
A.4 B.8 C.12 D.16
4.菱形ABCD中,∠A∶∠B=1∶5,若周长为8,则此菱形的高等于( ).
A. B.4 C.1 D.2
5.如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=FC=5,BE=DF=12,则EF的长是( )
A.7 B.8 C. D.
6. 如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,则∠AEB的度数为( )
A.10° B.15° C.20° D.12.5°
二.填空题
7.矩形ABCD中,对角线AC、BD相交于O,∠AOB=60°,AC=10,则AB=______,BC=______.
8. 如图,将边长为2的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△,若两个三角形重叠部分的面积是1,则它移动的距离等于____.
9. 如图,边长为2的正方形ABCD的对角线相交于点O,过点O的直线分别交AD、BC于E、F,则阴影部分的面积是_______.
10.如图,两条等宽的长方形纸条倾斜的重叠着,已知长方形纸条宽度为3cm,∠ABC=60°,则四边形ABCD的面积为________cm2.
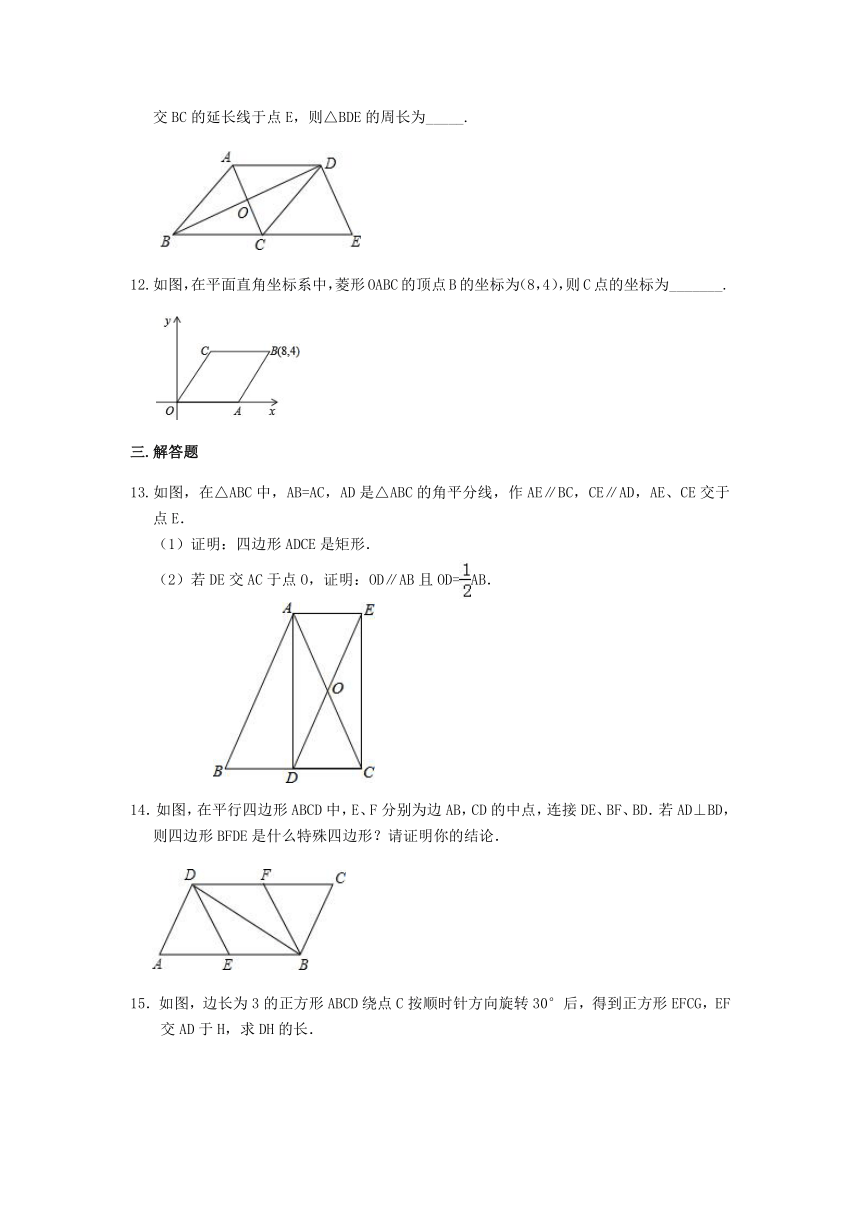
11. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,AC=10,过点D作DE∥AC交BC的延长线于点E,则△BDE的周长为_____.
12.如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则C点的坐标为_______.
三.解答题
13.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,作AE∥BC,CE∥AD,AE、CE交于点E.
(1)证明:四边形ADCE是矩形.
(2)若DE交AC于点O,证明:OD∥AB且OD=AB.
14.如图,在平行四边形ABCD中,E、F分别为边AB,CD的中点,连接DE、BF、BD.若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
15.如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后,得到正方形EFCG,EF交AD于H,求DH的长.
【答案与解析】
一.选择题
1.【答案】C;
【解析】矩形的对角线相等.
2.【答案】B;
【解析】直角三角形中,30°所对的边等于斜边的一半.
3.【答案】D;
【解析】BC=2EF=4,周长等于4BC=16.
4.【答案】C;
【解析】由题意,∠A=30°,边长为2,菱形的高等于×2=1.
5.【答案】C;
6.【答案】B;
【解析】根据等边三角形和正方形的性质可知AB=AE,∴∠BAE=90°+60°=150°,∴∠AEB=(180°-150°)÷2=15°.
二.填空题
7.【答案】5,5;
【解析】可证△AOB为等边三角形,AB=AO=CO=BO.
8.【答案】1;
【解析】移动距离为,重叠部分面积为CE×,所以,得,所以.
9.【答案】1;
【解析】由题可知△DEO≌△BFO,阴影面积就等于三角形BOC面积.
10.【答案】.
【解析】∵AB∥CD,AD∥BC,
??∴四边形ABCD是平行四边形,
???作AE⊥BC,AF⊥CD,
??∠ABC=∠ADF=60°,且AE=AF
??∴△ABE≌△ADF,
??∴AB=AD,即四边形ABCD是菱形.
??∵AE=3cm,
??∴BE=,
??∴BC=2BE=,
??∴S四边形ABCD=BC?AE=×3=cm2.
11.【答案】60;
【解析】因为菱形的对角线互相垂直及互相平分就可以在Rt△AOB中利用勾股定理求出OB=12,BD=2OB=24,DE=2OC=10,BE=2BC=26,△BDE的周长为60.
12.【答案】(3,4);
【解析】过B点作BD⊥OA于D,过C点作CE⊥OA于E,BD=4,OA=,AD=8-,,解得,所以OE=AD=8-5=3,C点坐标为(3,4).
三.解答题
13.【解析】
证明:(1)∵AB=AC,AD是△ABC的角平分线,
???∴AD⊥BC,且BD=CD,
???∵AE∥BC,CE∥AD,
???∴四边形ADCE是平行四边形,
???∴四边形ADCE是矩形;
(2)∵四边形ADCE是矩形,
???∴OA=OC,
???∴OD是△ABC的中位线,
???∴OD∥AB且OD=AB.
14.【解析】
四边形BFDE是菱形,
证明:∵AD⊥BD,
∴△ABD是直角三角形,且AB是斜边,
∵E为AB的中点,
∴DE=AB=BE,
∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵F为DC中点,E为AB中点,
∴DF=DC,BE=AB,
∴DF=BE,DF∥BE,
∴四边形DFBE是平行四边形,
∵DE=EB,
∴四边形BFDE是菱形.
15.【解析】
解:如图,连接CH,
∵正方形ABCD绕点C按顺时针方向旋转30°,
∴∠BCF=30°,则∠DCF=60°,
在Rt△CDH和Rt△CFH中,
∴Rt△CDH≌Rt△CFH,
∴∠DCH=∠FCH=∠DCF=30°,
在Rt△CDH中,DH=,CH=2,CD=,
∴DH=.
