北京版八年级下册数学课件15.3.1平行四边形的性质(第一课时)(共51张PPT)
文档属性
| 名称 | 北京版八年级下册数学课件15.3.1平行四边形的性质(第一课时)(共51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
图片预览







文档简介
(共51张PPT)
平行四边形的性质(第一课时)
初二年级 数学
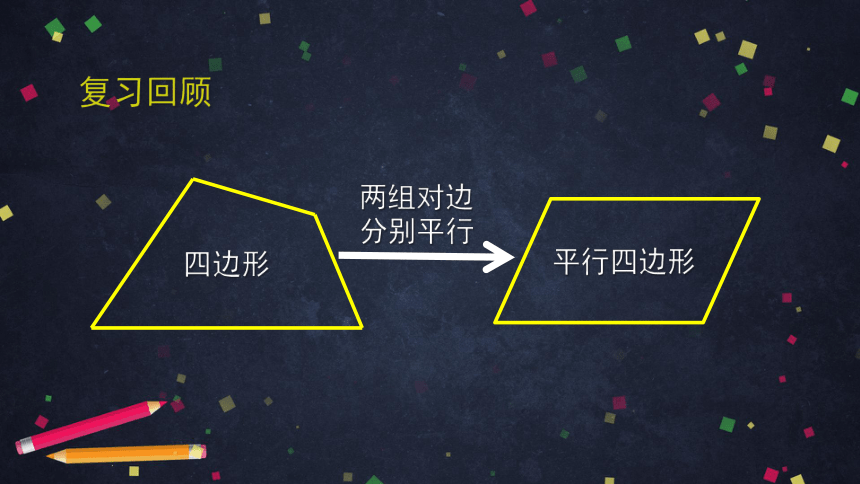
四边形
平行四边形
两组对边分别平行
复习回顾
A
B
C
D
复习回顾
定义(性质)平行四边形的对边平行.
符号语言:
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC .
A
B
C
D
观察猜想
平行四边形的对边相等.
A
B
C
D
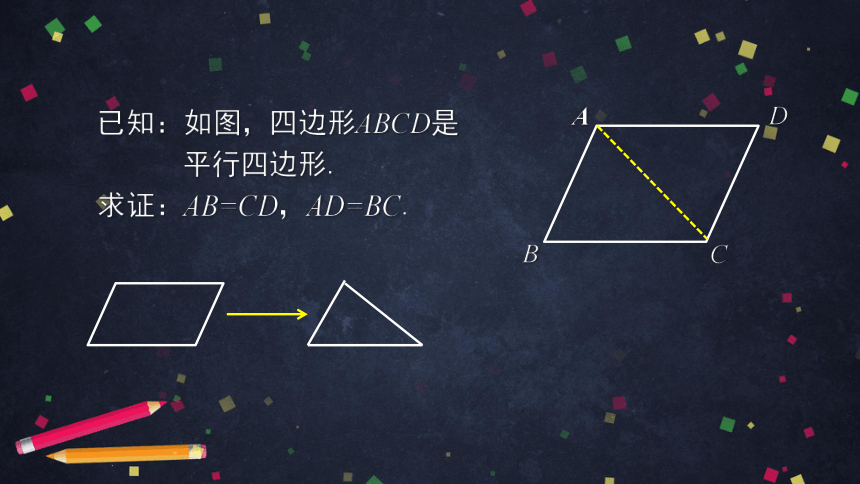
已知:如图,四边形ABCD是
平行四边形.
求证:AB=CD,AD=BC.
A
B
C
D
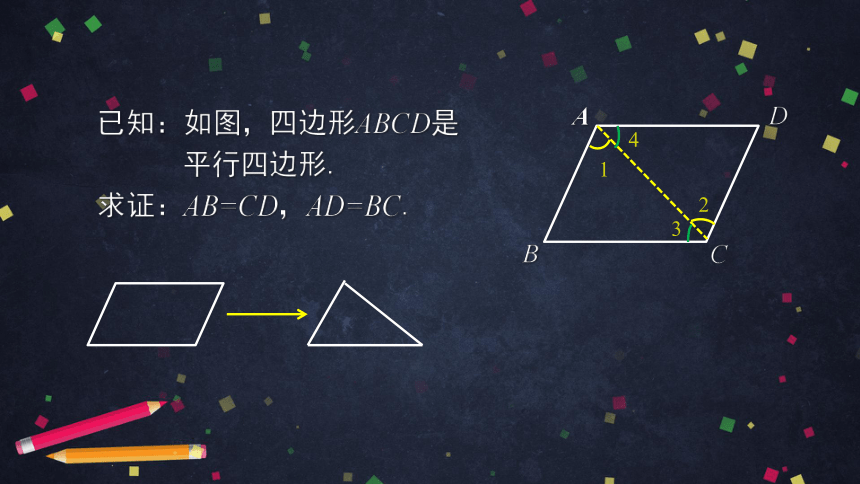
已知:如图,四边形ABCD是
平行四边形.
求证:AB=CD,AD=BC.
2
1
4
3
证明:连接AC.
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC.
∴ ∠1=∠2, ∠3=∠4.
又∵ AC=CA,
∴ △ABC≌△CDA.
∴ AB=CD,AD=BC.
1
2
4
3
A
B
C
D
平行四边形性质定理1
平行四边形的对边相等.
符号语言:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC .
A
B
C
D
A
B
C
D
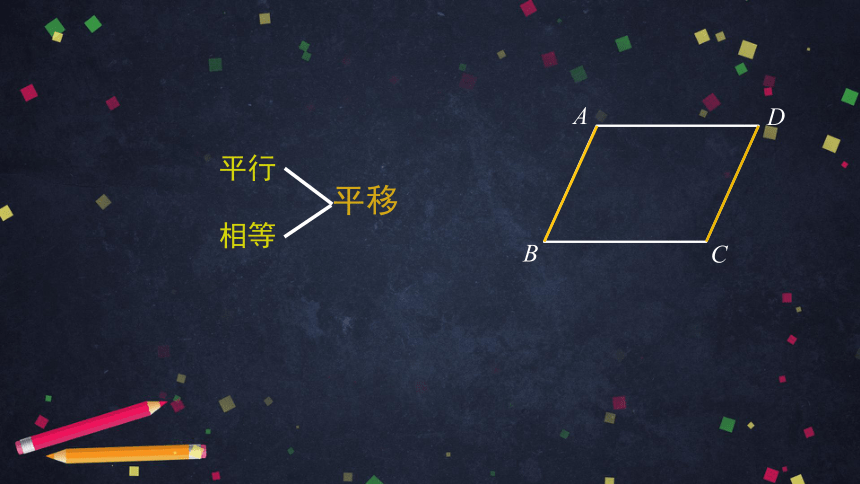
平移
相等
平行
如图,E,F 是 ABCD 的对角线AC上两点,且AE = CF.
请你写出图中的一对全等三角形,并对此加以证明.
△ABE≌△CDF,△ABC≌△CDA , △ADF≌△CBE.
例题
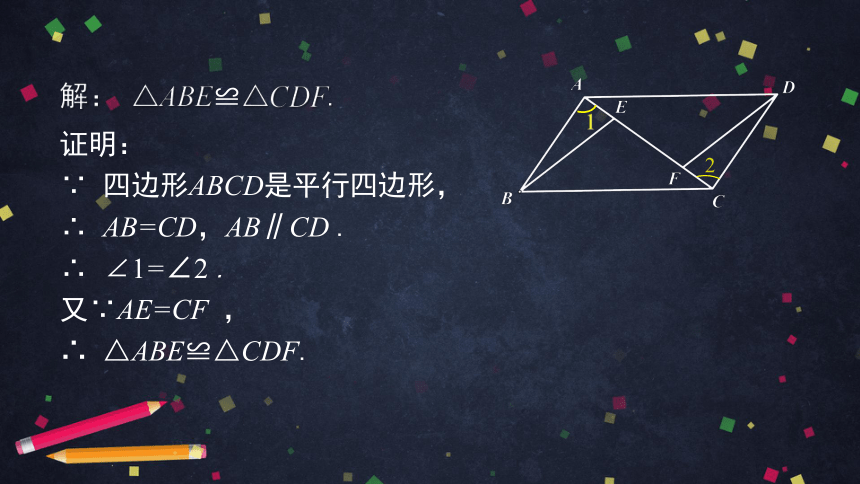
解: △ABE≌△CDF.
1
2
解: △ABE≌△CDF.
证明:
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD .
∴ ∠1=∠2 .
又∵AE=CF ,
∴ △ABE≌△CDF.
如图,小迪用一根36米长的绳子围成了一个平行四边形的场地,其中一条边AB长为8米,则CD=____米,BC=____米.
A
B
C
D
10
10
8
8
8
10
练习
(1)如图,直线l1∥l2 ,AB和CD是夹在 l1,l2 之间的平行线段,AB和CD的长度有什么关系?为什么?
相等
例题
(1)如图,直线l1∥l2 ,AB和CD是夹在 l1,l2 之间的平行线段,AB和CD的长度有什么关系?为什么?
例题
证明:
∵ AB∥CD , AD∥BC ,
∴ 四边形ABCD是平行四边形.
∴ AB=CD.
结论
夹在两条平行线间的平行线段相等.
结论
夹在两条平行线间的平行线段相等.
(2)如图,l1∥ l2 ,A ,D 是l1上不同的两点,线段AB和CD 的长度分别是点A,D 到l2的距离,AB与CD的长度有什么关系?为什么?
例题
(2)如图,l1∥ l2 ,A ,D 是l1上不同的两点,线段AB和CD 的长度分别是点A,D 到l2的距离,AB与CD的长度有什么关系?为什么?
例题
(2)如图,l1∥ l2 ,A ,D 是l1上不同的两点,线段AB和CD 的长度分别是点A,D 到l2的距离,AB与CD的长度有什么关系?为什么?
例题
(2)如图,l1∥ l2 ,A ,D 是l1上不同的两点,线段AB和CD 的长度分别是点A,D 到l2的距离,AB与CD的长度有什么关系?为什么?
相等
例题
证明:∵ 线段AB和CD的长度分别
是点A,D 到l2的距离,
∴ AB⊥l2 ,CD⊥l2 .
∴ AB∥CD.
∵ l1∥ l2 ,
∴ AB=CD.
两条平行线间的距离:
两条平行线中,一条直线上任意一点到另一条直线的距离.
两点的距离
点到直线的距离
两平行线间的距离
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
2
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
2
知识链接
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
两点的距离
点到直线的距离
两平行线间的距离
距离——数与形
结论
平行线间的距离处处相等.
夹在两根笔直的铁轨之间的
枕木是否一样长______,依据______________________
平行线间的距离处处相等.
是
实际应用
如图, 如果直线l1∥l2,那么△ABC的面积和△DBC 的面积是相等的.你能说出理由吗?你还能在这两条平行线l1,l2之间画出其他与△ABC面积相等的三角形吗?
知识拓展
如图, 如果直线l1∥l2,那么△ABC的面积和△DBC 的面积是相等的.你能说出理由吗?你还能在这两条平行线l1,l2之间画出其他与△ABC面积相等的三角形吗?
知识拓展
E
F
同底等高的两个三角形面积相等
如图, 如果直线l1∥l2,那么△ABC的面积和△DBC 的面积是相等的.你能说出理由吗?你还能在这两条平行线l1,l2之间画出其他与△ABC面积相等的三角形吗?
知识拓展
P
同底等高的两个三角形面积相等
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
巩固练习
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
1
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
1
证明:∵DE∥AC,DF∥AB ,
∴四边形AEDF是平行四边形,∠C=∠1 .
∴AE=DF.
∵AB = AC ,
∴∠B=∠C.
∴∠B=∠1.
∴BE=DE.
∴DE+DF=BE+AE=AB.
1
2.如图,AD∥BC,AE∥CD,
BD平分∠ABC.
求证:AB=CE.
巩固练习
巩固练习
2.如图,AD∥BC,AE∥CD,
BD平分∠ABC.
求证:AB=CE.
巩固练习
2.如图,AD∥BC,AE∥CD,
BD平分∠ABC.
求证:AB=CE.
证明:∵BD平分∠ABC ,
∴ ∠1=∠2.
∵AD∥BC ,
∴∠1=∠3.
∴∠2=∠3.
∴AB=AD.
1
2
3
∵AD∥BC,AE∥CD ,
∴四边形AECD是平行四边形.
∴AD=CE.
∴AB=CE.
1
2
3
1.平行四边形的边的性质
对边平行
对边相等
2.两个推论
夹在两条平行线间的平行线段相等
平行线间的距离处处相等
3.三个相关距离的概念
点到点
点到线
线到线(平行)
知识梳理
作 业
1.已知:平行四边形ABCD的周长60cm , AB=12cm ,
那么CD=_____cm,BC=_____cm.
2.平行四边形ABCD的周长35cm,AB:BC=3:4,
那么AB=_____cm,BC=_____cm.
3.在□ABCD中,AE⊥BC于E ,
且BE=CE ,□ABCD的周长为3.6米,
△ABC的周长为2.8米,求:
□ABCD的各边长和AE的长.
作 业
你认真学习的样子最美!
平行四边形的性质(第一课时)
初二年级 数学
四边形
平行四边形
两组对边分别平行
复习回顾
A
B
C
D
复习回顾
定义(性质)平行四边形的对边平行.
符号语言:
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC .
A
B
C
D
观察猜想
平行四边形的对边相等.
A
B
C
D
已知:如图,四边形ABCD是
平行四边形.
求证:AB=CD,AD=BC.
A
B
C
D
已知:如图,四边形ABCD是
平行四边形.
求证:AB=CD,AD=BC.
2
1
4
3
证明:连接AC.
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC.
∴ ∠1=∠2, ∠3=∠4.
又∵ AC=CA,
∴ △ABC≌△CDA.
∴ AB=CD,AD=BC.
1
2
4
3
A
B
C
D
平行四边形性质定理1
平行四边形的对边相等.
符号语言:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC .
A
B
C
D
A
B
C
D
平移
相等
平行
如图,E,F 是 ABCD 的对角线AC上两点,且AE = CF.
请你写出图中的一对全等三角形,并对此加以证明.
△ABE≌△CDF,△ABC≌△CDA , △ADF≌△CBE.
例题
解: △ABE≌△CDF.
1
2
解: △ABE≌△CDF.
证明:
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD .
∴ ∠1=∠2 .
又∵AE=CF ,
∴ △ABE≌△CDF.
如图,小迪用一根36米长的绳子围成了一个平行四边形的场地,其中一条边AB长为8米,则CD=____米,BC=____米.
A
B
C
D
10
10
8
8
8
10
练习
(1)如图,直线l1∥l2 ,AB和CD是夹在 l1,l2 之间的平行线段,AB和CD的长度有什么关系?为什么?
相等
例题
(1)如图,直线l1∥l2 ,AB和CD是夹在 l1,l2 之间的平行线段,AB和CD的长度有什么关系?为什么?
例题
证明:
∵ AB∥CD , AD∥BC ,
∴ 四边形ABCD是平行四边形.
∴ AB=CD.
结论
夹在两条平行线间的平行线段相等.
结论
夹在两条平行线间的平行线段相等.
(2)如图,l1∥ l2 ,A ,D 是l1上不同的两点,线段AB和CD 的长度分别是点A,D 到l2的距离,AB与CD的长度有什么关系?为什么?
例题
(2)如图,l1∥ l2 ,A ,D 是l1上不同的两点,线段AB和CD 的长度分别是点A,D 到l2的距离,AB与CD的长度有什么关系?为什么?
例题
(2)如图,l1∥ l2 ,A ,D 是l1上不同的两点,线段AB和CD 的长度分别是点A,D 到l2的距离,AB与CD的长度有什么关系?为什么?
例题
(2)如图,l1∥ l2 ,A ,D 是l1上不同的两点,线段AB和CD 的长度分别是点A,D 到l2的距离,AB与CD的长度有什么关系?为什么?
相等
例题
证明:∵ 线段AB和CD的长度分别
是点A,D 到l2的距离,
∴ AB⊥l2 ,CD⊥l2 .
∴ AB∥CD.
∵ l1∥ l2 ,
∴ AB=CD.
两条平行线间的距离:
两条平行线中,一条直线上任意一点到另一条直线的距离.
两点的距离
点到直线的距离
两平行线间的距离
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
2
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
2
知识链接
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
知识链接
将直线 y=x 向上平移2个单位后,所得的直线为y=x+2 ,这两条直线间的距离为_____.
两点的距离
点到直线的距离
两平行线间的距离
距离——数与形
结论
平行线间的距离处处相等.
夹在两根笔直的铁轨之间的
枕木是否一样长______,依据______________________
平行线间的距离处处相等.
是
实际应用
如图, 如果直线l1∥l2,那么△ABC的面积和△DBC 的面积是相等的.你能说出理由吗?你还能在这两条平行线l1,l2之间画出其他与△ABC面积相等的三角形吗?
知识拓展
如图, 如果直线l1∥l2,那么△ABC的面积和△DBC 的面积是相等的.你能说出理由吗?你还能在这两条平行线l1,l2之间画出其他与△ABC面积相等的三角形吗?
知识拓展
E
F
同底等高的两个三角形面积相等
如图, 如果直线l1∥l2,那么△ABC的面积和△DBC 的面积是相等的.你能说出理由吗?你还能在这两条平行线l1,l2之间画出其他与△ABC面积相等的三角形吗?
知识拓展
P
同底等高的两个三角形面积相等
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
巩固练习
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
1
巩固练习
1.如图,在△ABC 中,AB = AC,
DE∥AC,DF∥AB.
求证:DE + DF = AB.
1
证明:∵DE∥AC,DF∥AB ,
∴四边形AEDF是平行四边形,∠C=∠1 .
∴AE=DF.
∵AB = AC ,
∴∠B=∠C.
∴∠B=∠1.
∴BE=DE.
∴DE+DF=BE+AE=AB.
1
2.如图,AD∥BC,AE∥CD,
BD平分∠ABC.
求证:AB=CE.
巩固练习
巩固练习
2.如图,AD∥BC,AE∥CD,
BD平分∠ABC.
求证:AB=CE.
巩固练习
2.如图,AD∥BC,AE∥CD,
BD平分∠ABC.
求证:AB=CE.
证明:∵BD平分∠ABC ,
∴ ∠1=∠2.
∵AD∥BC ,
∴∠1=∠3.
∴∠2=∠3.
∴AB=AD.
1
2
3
∵AD∥BC,AE∥CD ,
∴四边形AECD是平行四边形.
∴AD=CE.
∴AB=CE.
1
2
3
1.平行四边形的边的性质
对边平行
对边相等
2.两个推论
夹在两条平行线间的平行线段相等
平行线间的距离处处相等
3.三个相关距离的概念
点到点
点到线
线到线(平行)
知识梳理
作 业
1.已知:平行四边形ABCD的周长60cm , AB=12cm ,
那么CD=_____cm,BC=_____cm.
2.平行四边形ABCD的周长35cm,AB:BC=3:4,
那么AB=_____cm,BC=_____cm.
3.在□ABCD中,AE⊥BC于E ,
且BE=CE ,□ABCD的周长为3.6米,
△ABC的周长为2.8米,求:
□ABCD的各边长和AE的长.
作 业
你认真学习的样子最美!
同课章节目录
