北京版八年级下册数学15.2平行四边形与特殊的平行四边形课件 (共94张PPT)
文档属性
| 名称 | 北京版八年级下册数学15.2平行四边形与特殊的平行四边形课件 (共94张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
图片预览











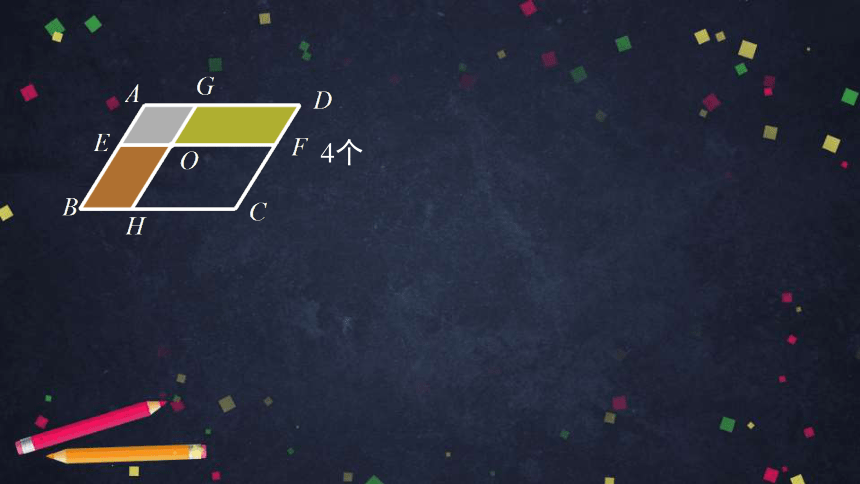
文档简介
(共94张PPT)
初二年级 数学
平行四边形与特殊的平行四边形
一、知识概要
二、关键问题
三、典型例题
一、知识概要
二、关键问题
三、典型例题
一、知识概要
思考小学我们学习过哪些四边形?
一、知识概要
思考小学我们学习过哪些四边形?
平行四边形
长方形
菱形
梯形
正方形
平行四边形
梯形
只有一组对边平行
两组对边分别平行
四边形
一、知识概要
二、关键问题
三、典型例题
1.平行四边形的概念.
2.特殊的平行四边形的概念.
3.平行四边形与特殊的平行四边形的关系.
二、关键问题
1.平行四边形的概念.
二、关键问题
两组对边分别平行的四边形叫做平行四边形.
1.平行四边形的概念.
二、关键问题
两组对边分别平行的四边形叫做平行四边形.
平行四边形是特殊的四边形.
如图,在四边形ABCD中,
如果AB∥DC, AD∥BC,
那么四边形ABCD就是平行四边形.
记作“□ABCD”.
如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O. 试找出图中的平行四边形.
4个
4个
2个
4个
2个
2个
4个
2个
2个
1个
如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O. 试找出图中的平行四边形.
解:
9个.
二、关键问题
在什么地方见到过平行四边形的形象?
1.平行四边形的概念.
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
2.特殊的平行四边形的概念.
二、关键问题
2.特殊的平行四边形的概念.
二、关键问题
有一个角是直角的平行四边形叫做矩形.
2.特殊的平行四边形的概念.
二、关键问题
有一个角是直角的四边形是矩形吗?
不确定.
2.特殊的平行四边形的概念.
二、关键问题
有四个角是直角的平行四边形是矩形?
实际上,用“一个角是直角”可以推出其余三个角是直角,不需要多余条件.
2.特殊的平行四边形的概念.
二、关键问题
在什么地方见到过矩形的形象?
2.特殊的平行四边形的概念.
二、关键问题
2.特殊的平行四边形的概念.
二、关键问题
有一组邻边相等的平行四边形叫做菱形.
2.特殊的平行四边形的概念.
二、关键问题
在什么地方见到过菱形的形象?
2.特殊的平行四边形的概念.
二、关键问题
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
完美正方形
2.特殊的平行四边形的概念.
二、关键问题
在什么地方见到过正方形的形象?
2.特殊的平行四边形的概念.
二、关键问题
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
3.平行四边形与特殊的平行四边形的关系
二、关键问题
平行四边形
矩形
菱形
正方形
平行四边形
一个直角
矩形
平行四边形
一个直角
矩形
平行四边形
菱形
一组邻边相等
一个直角
矩形
平行四边形
正方形
菱形
一组邻边相等
一个直角
一组邻边相等
一个直角
矩形
平行四边形
正方形
菱形
一组邻边相等
一组邻边相等
一个直角
一组邻边相等
一个直角
矩形
平行四边形
正方形
菱形
一个直角
一组邻边相等
一组邻边相等
一个直角
一组邻边相等
一、知识概要
二、关键问题
三、典型例题
例 填空题:
(1)正方形是 的四边形;
(2)正方形是 的平行四边形;
(3)正方形是 的矩形;
(4)正方形是 的菱形.
三、典型例题
(1)正方形是 的四边形;
三、典型例题
有两组对边分别平行,
并且有一组邻边相等,
有一个角是直角
例 填空题:
(1)正方形是 的四边形;
三、典型例题
例 填空题:
(1)正方形是 的四边形;
三、典型例题
四边相等且四个角都是直角
例 填空题:
(1)正方形是 的四边形;
三、典型例题
四边相等且四个角都是直角
有一组邻边相等并且有一个角是直角
(2)正方形是 的
平行四边形;
例 填空题:
(1)正方形是 的四边形;
三、典型例题
四边相等且四个角都是直角
有一组邻边相等并且有一个角是直角
有一组邻边相等
(3)正方形是 的矩形;
(2)正方形是 的
平行四边形;
例 填空题:
(1)正方形是 的四边形;
三、典型例题
四边相等且四个角都是直角
有一组邻边相等并且有一个角是直角
有一组邻边相等
有一个角是直角
(4)正方形是 的菱形.
(3)正方形是 的矩形;
(2)正方形是 的
平行四边形;
平行四边形
正方形
平行四边形
正方形
一个直角
一组邻边相等
一个直角
矩形
平行四边形
正方形
一组邻边相等
一个直角
一组邻边相等
一个直角
矩形
平行四边形
正方形
菱形
一个直角
一组邻边相等
一组邻边相等
一个直角
一组邻边相等
例 如图,是8×8的正方形网格,每
个正方形的顶点为格点,每个小正方
形的边长均为1,在正方形网格中标
注了6个格点,这6个格点简称为标注
点.请在图中以4个标注点为顶点,画
一个平行四边形,并计算所画的平行
四边形的面积.
三、典型例题
例
三、典型例题
(1)
(2)
(3)
例
三、典型例题
公式法
例
三、典型例题
(1)
平行四边形的面积
=底×高
例
三、典型例题
=3×2=6.
(1)
平行四边形的面积
=底×高
例
三、典型例题
平行四边形的面积
=底×高
例
三、典型例题
(2)
例
三、典型例题
割补法
例
三、典型例题
平行四边形的面积
=矩形的面积
-4个三角形的面积
=6.
(2)
例
三、典型例题
割补法
例
三、典型例题
(3)
平行四边形的面积
=矩形的面积
-4个三角形的面积
=6.
三、典型例题
小结:计算面积的方法
公式法
割补法
例
三、典型例题
平行四边形的面积等于6.
例 图中有多少个正方形?有多少个矩形?
三、典型例题
(1)
(2)
例 图中有多少个正方形?有多少个矩形?
三、典型例题
(1)
例 图中有多少个正方形?
三、典型例题
(1)
4个
例 图中有多少个正方形?
三、典型例题
(1)
4个
1个
例 图中有多少个正方形?
三、典型例题
(1)
4个
1个
5个
例 图中有多少个矩形?
三、典型例题
(1)
5个
例 图中有多少个矩形?
三、典型例题
(1)
5个
2个
例 图中有多少个矩形?
三、典型例题
(1)
5个
2个
2个
例 图中有多少个矩形?
三、典型例题
(1)
5个
2个
2个
9个
例 图中有多少个正方形?有多少个矩形?
三、典型例题
(2)
例 图中有多少个正方形?
三、典型例题
(2)
9个
例 图中有多少个正方形?
三、典型例题
(2)
9个
4个
例 图中有多少个正方形?
三、典型例题
(2)
9个
1个
4个
例 图中有多少个正方形?
三、典型例题
(2)
9个
1个
4个
14个
例 图中有多少个矩形?
三、典型例题
(2)
例 图中有多少个矩形?
三、典型例题
(2)
6个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
3个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
3个
2个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
3个
2个
2个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
3个
2个
2个
36个
小结
研究图形问题时,
从左到右,
从上到下,
从少到多.
例 图中有多少个正方形?有多少个矩形?
三、典型例题
(1)
(2)
(1)5个正方形,9个矩形.
(2)14个正方形,36个矩形.
一个直角
矩形
平行四边形
正方形
菱形
一个直角
一组邻边相等
一组邻边相等
一个直角
一组邻边相等
作业
1.说明矩形、菱形、正方形各是怎样特殊的平行四边形??
2.如图,以橙色格点为顶点,你能画出多少个平行四边形?
作业
3.根据一道习题可知:过平行四边形
纸片的一个顶点,作一条线段,沿这条
线段剪下这个三角形纸片,将它平移到
右边的位置,平移距离等于平行四边形
的底边长a,可得到一个矩形如图1.
作业
在图2的纸片中,按上述方法,你能使
所得的四边形是菱形吗?如果能,作
出这条线段及平移后的三角形(用阴影
表示),并简要说明作线段方法;如果
不能,请说明理由.
图2
初二年级 数学
平行四边形与特殊的平行四边形
一、知识概要
二、关键问题
三、典型例题
一、知识概要
二、关键问题
三、典型例题
一、知识概要
思考小学我们学习过哪些四边形?
一、知识概要
思考小学我们学习过哪些四边形?
平行四边形
长方形
菱形
梯形
正方形
平行四边形
梯形
只有一组对边平行
两组对边分别平行
四边形
一、知识概要
二、关键问题
三、典型例题
1.平行四边形的概念.
2.特殊的平行四边形的概念.
3.平行四边形与特殊的平行四边形的关系.
二、关键问题
1.平行四边形的概念.
二、关键问题
两组对边分别平行的四边形叫做平行四边形.
1.平行四边形的概念.
二、关键问题
两组对边分别平行的四边形叫做平行四边形.
平行四边形是特殊的四边形.
如图,在四边形ABCD中,
如果AB∥DC, AD∥BC,
那么四边形ABCD就是平行四边形.
记作“□ABCD”.
如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O. 试找出图中的平行四边形.
4个
4个
2个
4个
2个
2个
4个
2个
2个
1个
如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O. 试找出图中的平行四边形.
解:
9个.
二、关键问题
在什么地方见到过平行四边形的形象?
1.平行四边形的概念.
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
1.平行四边形的概念.
二、关键问题
如何画出平行四边形?
2.特殊的平行四边形的概念.
二、关键问题
2.特殊的平行四边形的概念.
二、关键问题
有一个角是直角的平行四边形叫做矩形.
2.特殊的平行四边形的概念.
二、关键问题
有一个角是直角的四边形是矩形吗?
不确定.
2.特殊的平行四边形的概念.
二、关键问题
有四个角是直角的平行四边形是矩形?
实际上,用“一个角是直角”可以推出其余三个角是直角,不需要多余条件.
2.特殊的平行四边形的概念.
二、关键问题
在什么地方见到过矩形的形象?
2.特殊的平行四边形的概念.
二、关键问题
2.特殊的平行四边形的概念.
二、关键问题
有一组邻边相等的平行四边形叫做菱形.
2.特殊的平行四边形的概念.
二、关键问题
在什么地方见到过菱形的形象?
2.特殊的平行四边形的概念.
二、关键问题
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
完美正方形
2.特殊的平行四边形的概念.
二、关键问题
在什么地方见到过正方形的形象?
2.特殊的平行四边形的概念.
二、关键问题
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
3.平行四边形与特殊的平行四边形的关系
二、关键问题
平行四边形
矩形
菱形
正方形
平行四边形
一个直角
矩形
平行四边形
一个直角
矩形
平行四边形
菱形
一组邻边相等
一个直角
矩形
平行四边形
正方形
菱形
一组邻边相等
一个直角
一组邻边相等
一个直角
矩形
平行四边形
正方形
菱形
一组邻边相等
一组邻边相等
一个直角
一组邻边相等
一个直角
矩形
平行四边形
正方形
菱形
一个直角
一组邻边相等
一组邻边相等
一个直角
一组邻边相等
一、知识概要
二、关键问题
三、典型例题
例 填空题:
(1)正方形是 的四边形;
(2)正方形是 的平行四边形;
(3)正方形是 的矩形;
(4)正方形是 的菱形.
三、典型例题
(1)正方形是 的四边形;
三、典型例题
有两组对边分别平行,
并且有一组邻边相等,
有一个角是直角
例 填空题:
(1)正方形是 的四边形;
三、典型例题
例 填空题:
(1)正方形是 的四边形;
三、典型例题
四边相等且四个角都是直角
例 填空题:
(1)正方形是 的四边形;
三、典型例题
四边相等且四个角都是直角
有一组邻边相等并且有一个角是直角
(2)正方形是 的
平行四边形;
例 填空题:
(1)正方形是 的四边形;
三、典型例题
四边相等且四个角都是直角
有一组邻边相等并且有一个角是直角
有一组邻边相等
(3)正方形是 的矩形;
(2)正方形是 的
平行四边形;
例 填空题:
(1)正方形是 的四边形;
三、典型例题
四边相等且四个角都是直角
有一组邻边相等并且有一个角是直角
有一组邻边相等
有一个角是直角
(4)正方形是 的菱形.
(3)正方形是 的矩形;
(2)正方形是 的
平行四边形;
平行四边形
正方形
平行四边形
正方形
一个直角
一组邻边相等
一个直角
矩形
平行四边形
正方形
一组邻边相等
一个直角
一组邻边相等
一个直角
矩形
平行四边形
正方形
菱形
一个直角
一组邻边相等
一组邻边相等
一个直角
一组邻边相等
例 如图,是8×8的正方形网格,每
个正方形的顶点为格点,每个小正方
形的边长均为1,在正方形网格中标
注了6个格点,这6个格点简称为标注
点.请在图中以4个标注点为顶点,画
一个平行四边形,并计算所画的平行
四边形的面积.
三、典型例题
例
三、典型例题
(1)
(2)
(3)
例
三、典型例题
公式法
例
三、典型例题
(1)
平行四边形的面积
=底×高
例
三、典型例题
=3×2=6.
(1)
平行四边形的面积
=底×高
例
三、典型例题
平行四边形的面积
=底×高
例
三、典型例题
(2)
例
三、典型例题
割补法
例
三、典型例题
平行四边形的面积
=矩形的面积
-4个三角形的面积
=6.
(2)
例
三、典型例题
割补法
例
三、典型例题
(3)
平行四边形的面积
=矩形的面积
-4个三角形的面积
=6.
三、典型例题
小结:计算面积的方法
公式法
割补法
例
三、典型例题
平行四边形的面积等于6.
例 图中有多少个正方形?有多少个矩形?
三、典型例题
(1)
(2)
例 图中有多少个正方形?有多少个矩形?
三、典型例题
(1)
例 图中有多少个正方形?
三、典型例题
(1)
4个
例 图中有多少个正方形?
三、典型例题
(1)
4个
1个
例 图中有多少个正方形?
三、典型例题
(1)
4个
1个
5个
例 图中有多少个矩形?
三、典型例题
(1)
5个
例 图中有多少个矩形?
三、典型例题
(1)
5个
2个
例 图中有多少个矩形?
三、典型例题
(1)
5个
2个
2个
例 图中有多少个矩形?
三、典型例题
(1)
5个
2个
2个
9个
例 图中有多少个正方形?有多少个矩形?
三、典型例题
(2)
例 图中有多少个正方形?
三、典型例题
(2)
9个
例 图中有多少个正方形?
三、典型例题
(2)
9个
4个
例 图中有多少个正方形?
三、典型例题
(2)
9个
1个
4个
例 图中有多少个正方形?
三、典型例题
(2)
9个
1个
4个
14个
例 图中有多少个矩形?
三、典型例题
(2)
例 图中有多少个矩形?
三、典型例题
(2)
6个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
3个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
3个
2个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
3个
2个
2个
例 图中有多少个矩形?
三、典型例题
(2)
6个
6个
3个
3个
2个
2个
36个
小结
研究图形问题时,
从左到右,
从上到下,
从少到多.
例 图中有多少个正方形?有多少个矩形?
三、典型例题
(1)
(2)
(1)5个正方形,9个矩形.
(2)14个正方形,36个矩形.
一个直角
矩形
平行四边形
正方形
菱形
一个直角
一组邻边相等
一组邻边相等
一个直角
一组邻边相等
作业
1.说明矩形、菱形、正方形各是怎样特殊的平行四边形??
2.如图,以橙色格点为顶点,你能画出多少个平行四边形?
作业
3.根据一道习题可知:过平行四边形
纸片的一个顶点,作一条线段,沿这条
线段剪下这个三角形纸片,将它平移到
右边的位置,平移距离等于平行四边形
的底边长a,可得到一个矩形如图1.
作业
在图2的纸片中,按上述方法,你能使
所得的四边形是菱形吗?如果能,作
出这条线段及平移后的三角形(用阴影
表示),并简要说明作线段方法;如果
不能,请说明理由.
图2
同课章节目录
