北京版八年级下册数学14.7一次函数的应用课件(第四课时) (共38张PPT)
文档属性
| 名称 | 北京版八年级下册数学14.7一次函数的应用课件(第四课时) (共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:20:04 | ||
图片预览









文档简介
(共38张PPT)
初二年级 数学
一次函数的应用(第四课时)
数形结合
O
y
x
一次函数
?
三角形
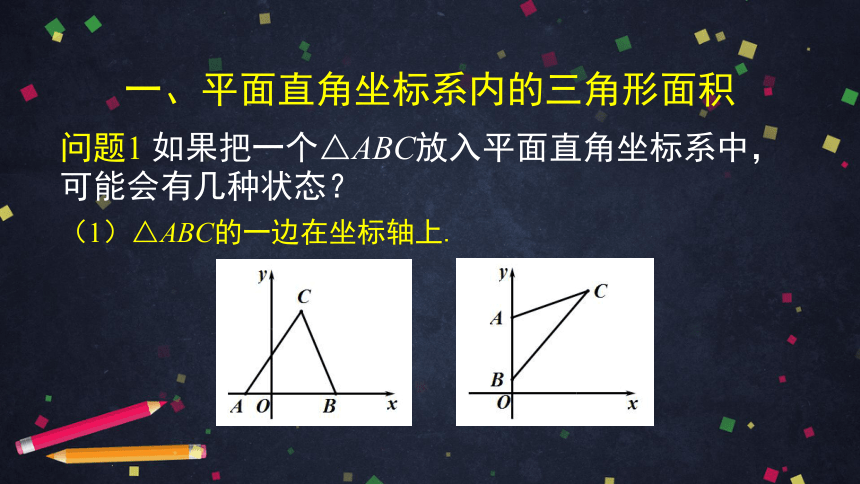
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
顶点
象限内
坐标轴上
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
(1)△ABC的一边在坐标轴上.
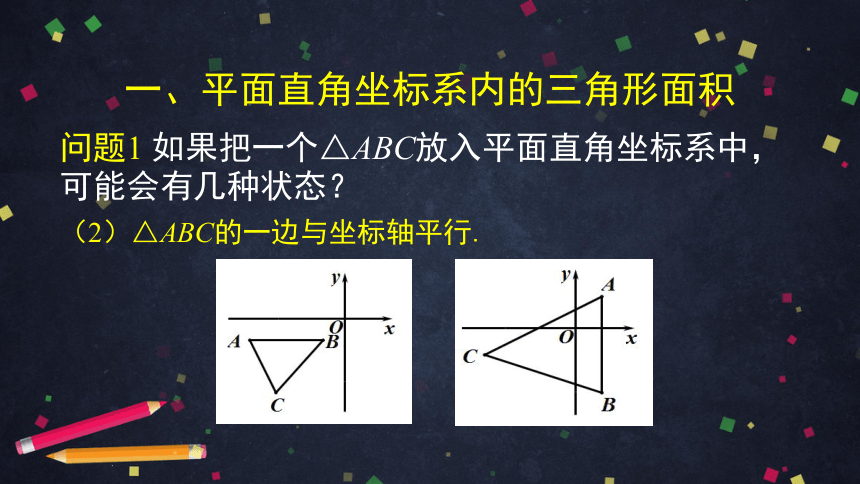
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
(2)△ABC的一边与坐标轴平行.
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
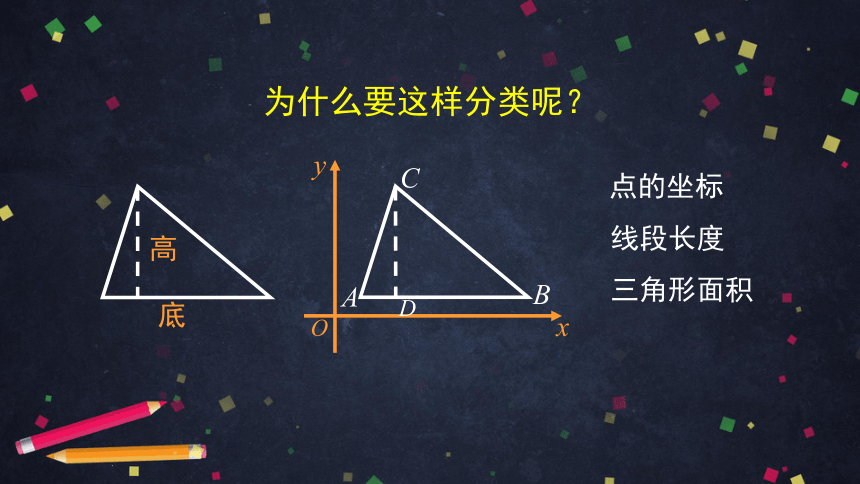
为什么要这样分类呢?
底
高
O
y
x
C
A
B
D
点的坐标
线段长度
三角形面积
问题2 计算△ABC的面积.
(1)△ABC的一边在坐标轴上.
已知A(-2,0),B(4,0),C(2,5)
线段AB的长度是两点间的横向距离,用两点的横坐标作差即可得到AB=4-(-2)=6.
你能够最先计算出来的是哪条边的长度?
问题2 计算△ABC的面积.
(1)△ABC的一边在坐标轴上.
D
解:∵底边AB=4-(-2)=6,
∴高是点C到x轴的距离CD=5.
又D(2,0),
已知A(-2,0),B(4,0),C(2,5)
问题2 计算△ABC的面积.
(1)△ABC的一边在坐标轴上.
D
已知A(0,0),B(4,0),C(2,5)
解:∵底边AB=4-0=4 ,
∴高是点C到x轴的距离CD=5.
又D(2,0),
问题2 计算△ABC的面积.
(1)△ABC的一边在坐标轴上.
D
已知A(0,4),B(0,1)C(3,5)
解:∵底边AB=4-1=3 ,
∴高是点C到y轴的距离CD=3.
又D(0,5),
问题2 计算△ABC的面积.
(2)△ABC的一边与坐标轴平行.
D
已知A(-6,-2),B(-1,-2),C(-4,-5)
∴高是点C到AB边的距离,
即CD=-2-(-5)=3
解:∵底边AB=-1-(-6)=5
又D(-4,-2)
问题2 计算△ABC的面积.
(2)△ABC的一边与坐标轴平行.
D
已知A(m,2),B( m,-4),C(-5,-2)
∴高是点C到AB边的距离,
即CD=m-(-5)=m+5
解:∵底边AB=2-(-4)=6
又D(m,-2)
D
问题2 计算△ABC的面积.
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
D
E
∵在直角梯形ADEC中,AD∥CE∥y轴,DE∥x轴
∴
如何计算坐标系内的三角形面积?
首先,要观察三角形各个顶点坐标的特点.
其次,明确三角形的底和高.为了方便计算尽量选用与坐标轴关系较紧密的边做底.如果没有符合要求的底和高,就尽可能构造容易计算出面积的特殊图形,来辅助计算.
问题2 计算△ABC的面积.
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
二、一条直线与坐标轴围成的三角形面积
例1 直线y=-5x+2与x轴交点坐标是 ,
与y轴交点坐标是 ,直线与两坐标轴围成三角形的面积是 .
(0,2)
( ,0)
直线
交点坐标
边长
面积
例2 直线AB与y轴交于点B(0,-2),点A在第一象限的角平分线上,且 ,求直线AB的表达式.
解:设直线AB的表达式为y=kx+b(k≠0).
点A坐标(a,a)(a>0)
例1
例2 直线AB与y轴交于点B(0,-2),点A在第一象限的角平分线上,且 ,求直线AB的表达式.
解:设直线AB的表达式为y=kx+b(k≠0).
点A坐标(a,a)(a>0)
∵直线AB与y轴交于点B(0,-2)
∴OB=2
a
例2 直线AB与y轴交于点B(0,-2),点A在第一象限的角平分线上,且 ,求直线AB的表达式.
∵
∴
解得a=2,点A坐标为(2,2)
待定系数法得直线AB的表达式为y=2x-2.
a
直线
交点坐标
边长
面积
底和高
线段长
点的坐标
例3 一次函数图象与y轴交点的纵坐标为-3,且与坐标轴围成的三角形面积为3,求其表达式,并画出图象.
解:∵一次函数图象与y轴交点的
纵坐标为-3,
∴设该交点为点B(0,-3),则有OB=3
设直线与x轴的交点为点A(a,0),则有OA=|a|.
∵
例3 一次函数图象与y轴交点的纵坐标为-3,且与坐标轴围成的三角形面积为3,求其表达式,并画出图象.
解得
∴
待定系数法得直线AB的表达式为
例3 一次函数图象与y轴交点的纵坐标为-3,且与坐标轴围成的三角形面积为3,求其表达式,并画出图象.
法2:设一次函数的表达式为y=kx+b(k≠0)
则直线与x轴交点A的坐标为(- ,0)
由题知
解得
∴直线AB的表达式为
直线
交点坐标
边长
面积
底和高
线段长
点的坐标
不确定
分类讨论
多条
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
(2)求△ABC的面积.
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
解: 把点A坐标代入直线y=kx-6,
得
解:由题知,点A坐标(4,0),点B坐标(1,0),则AB=3.
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(2)求△ABC的面积.
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
由
解得
∴点C坐标(2,-3)
∴
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,
且两直线交于点C.
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
直线
交点坐标
边长
面积
底和高
线段长
点的坐标
分类讨论
回顾总结
数形结合
位置
形状
特殊
布置作业
教材课后习题
布置作业
教材课后习题
布置作业
教材课后习题
同学们再见!
初二年级 数学
一次函数的应用(第四课时)
数形结合
O
y
x
一次函数
?
三角形
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
顶点
象限内
坐标轴上
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
(1)△ABC的一边在坐标轴上.
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
(2)△ABC的一边与坐标轴平行.
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
为什么要这样分类呢?
底
高
O
y
x
C
A
B
D
点的坐标
线段长度
三角形面积
问题2 计算△ABC的面积.
(1)△ABC的一边在坐标轴上.
已知A(-2,0),B(4,0),C(2,5)
线段AB的长度是两点间的横向距离,用两点的横坐标作差即可得到AB=4-(-2)=6.
你能够最先计算出来的是哪条边的长度?
问题2 计算△ABC的面积.
(1)△ABC的一边在坐标轴上.
D
解:∵底边AB=4-(-2)=6,
∴高是点C到x轴的距离CD=5.
又D(2,0),
已知A(-2,0),B(4,0),C(2,5)
问题2 计算△ABC的面积.
(1)△ABC的一边在坐标轴上.
D
已知A(0,0),B(4,0),C(2,5)
解:∵底边AB=4-0=4 ,
∴高是点C到x轴的距离CD=5.
又D(2,0),
问题2 计算△ABC的面积.
(1)△ABC的一边在坐标轴上.
D
已知A(0,4),B(0,1)C(3,5)
解:∵底边AB=4-1=3 ,
∴高是点C到y轴的距离CD=3.
又D(0,5),
问题2 计算△ABC的面积.
(2)△ABC的一边与坐标轴平行.
D
已知A(-6,-2),B(-1,-2),C(-4,-5)
∴高是点C到AB边的距离,
即CD=-2-(-5)=3
解:∵底边AB=-1-(-6)=5
又D(-4,-2)
问题2 计算△ABC的面积.
(2)△ABC的一边与坐标轴平行.
D
已知A(m,2),B( m,-4),C(-5,-2)
∴高是点C到AB边的距离,
即CD=m-(-5)=m+5
解:∵底边AB=2-(-4)=6
又D(m,-2)
D
问题2 计算△ABC的面积.
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
D
E
∵在直角梯形ADEC中,AD∥CE∥y轴,DE∥x轴
∴
如何计算坐标系内的三角形面积?
首先,要观察三角形各个顶点坐标的特点.
其次,明确三角形的底和高.为了方便计算尽量选用与坐标轴关系较紧密的边做底.如果没有符合要求的底和高,就尽可能构造容易计算出面积的特殊图形,来辅助计算.
问题2 计算△ABC的面积.
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
二、一条直线与坐标轴围成的三角形面积
例1 直线y=-5x+2与x轴交点坐标是 ,
与y轴交点坐标是 ,直线与两坐标轴围成三角形的面积是 .
(0,2)
( ,0)
直线
交点坐标
边长
面积
例2 直线AB与y轴交于点B(0,-2),点A在第一象限的角平分线上,且 ,求直线AB的表达式.
解:设直线AB的表达式为y=kx+b(k≠0).
点A坐标(a,a)(a>0)
例1
例2 直线AB与y轴交于点B(0,-2),点A在第一象限的角平分线上,且 ,求直线AB的表达式.
解:设直线AB的表达式为y=kx+b(k≠0).
点A坐标(a,a)(a>0)
∵直线AB与y轴交于点B(0,-2)
∴OB=2
a
例2 直线AB与y轴交于点B(0,-2),点A在第一象限的角平分线上,且 ,求直线AB的表达式.
∵
∴
解得a=2,点A坐标为(2,2)
待定系数法得直线AB的表达式为y=2x-2.
a
直线
交点坐标
边长
面积
底和高
线段长
点的坐标
例3 一次函数图象与y轴交点的纵坐标为-3,且与坐标轴围成的三角形面积为3,求其表达式,并画出图象.
解:∵一次函数图象与y轴交点的
纵坐标为-3,
∴设该交点为点B(0,-3),则有OB=3
设直线与x轴的交点为点A(a,0),则有OA=|a|.
∵
例3 一次函数图象与y轴交点的纵坐标为-3,且与坐标轴围成的三角形面积为3,求其表达式,并画出图象.
解得
∴
待定系数法得直线AB的表达式为
例3 一次函数图象与y轴交点的纵坐标为-3,且与坐标轴围成的三角形面积为3,求其表达式,并画出图象.
法2:设一次函数的表达式为y=kx+b(k≠0)
则直线与x轴交点A的坐标为(- ,0)
由题知
解得
∴直线AB的表达式为
直线
交点坐标
边长
面积
底和高
线段长
点的坐标
不确定
分类讨论
多条
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
(2)求△ABC的面积.
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
解: 把点A坐标代入直线y=kx-6,
得
解:由题知,点A坐标(4,0),点B坐标(1,0),则AB=3.
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(2)求△ABC的面积.
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
由
解得
∴点C坐标(2,-3)
∴
三、两条直线与坐标轴围成的三角形面积
例4 直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,
且两直线交于点C.
一、平面直角坐标系内的三角形面积
问题1 如果把一个△ABC放入平面直角坐标系中,可能会有几种状态?
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
(3)△ABC的任意一边不在坐标轴上且不与坐标轴平行.
直线
交点坐标
边长
面积
底和高
线段长
点的坐标
分类讨论
回顾总结
数形结合
位置
形状
特殊
布置作业
教材课后习题
布置作业
教材课后习题
布置作业
教材课后习题
同学们再见!
同课章节目录
