人教版八年级下册数学课件: 17.1勾股定理应用(第二课时)(共47张PPT)
文档属性
| 名称 | 人教版八年级下册数学课件: 17.1勾股定理应用(第二课时)(共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-18 19:57:25 | ||
图片预览





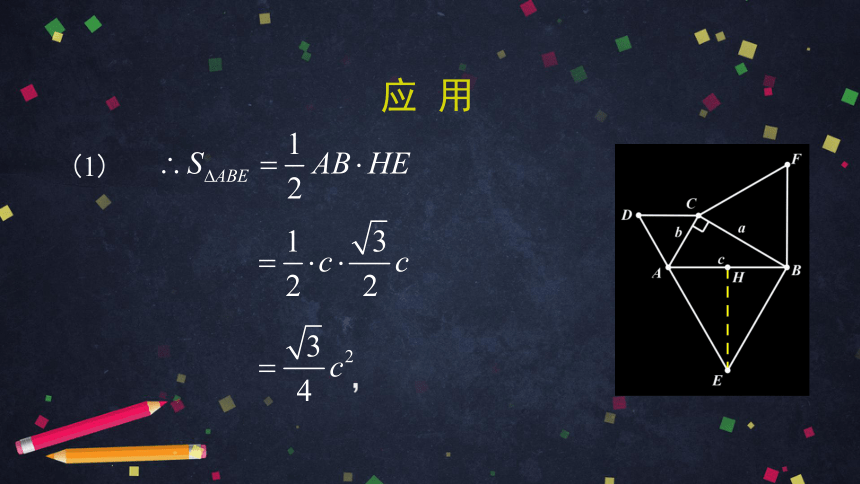

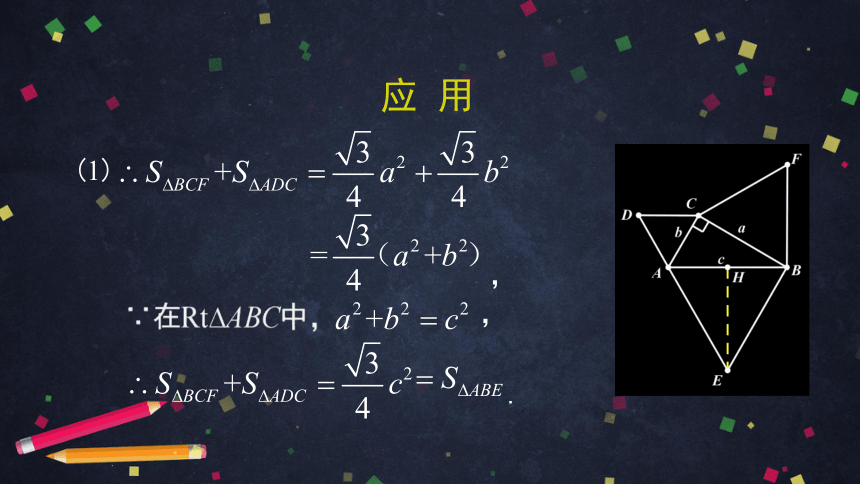

文档简介
(共47张PPT)
初二年级 数学
勾股定理应用(第二课时)
复习旧知
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么 .
勾股定理
∵在Rt 中,∠C=90°,(已知)
∴ .(勾股定理)
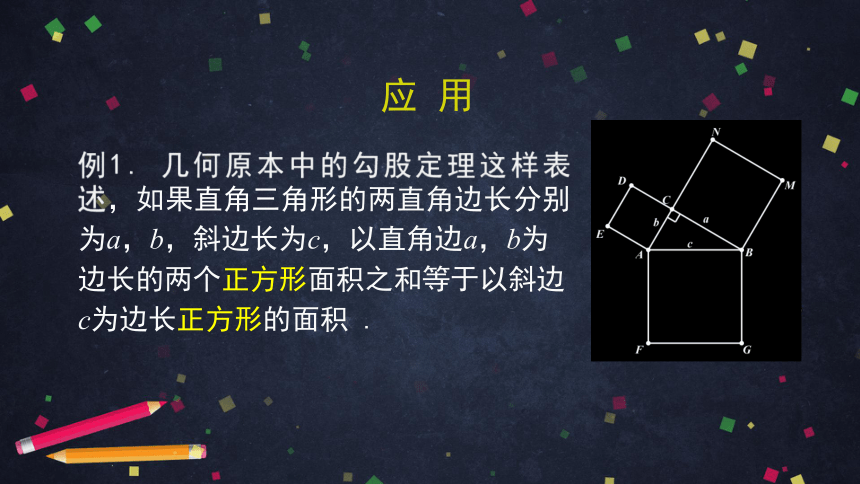
例1. 几何原本中的勾股定理这样表述,如果直角三角形的两直角边长分别
为a,b,斜边长为c,以直角边a,b为边长的两个正方形面积之和等于以斜边c为边长正方形的面积 .
应 用
应 用
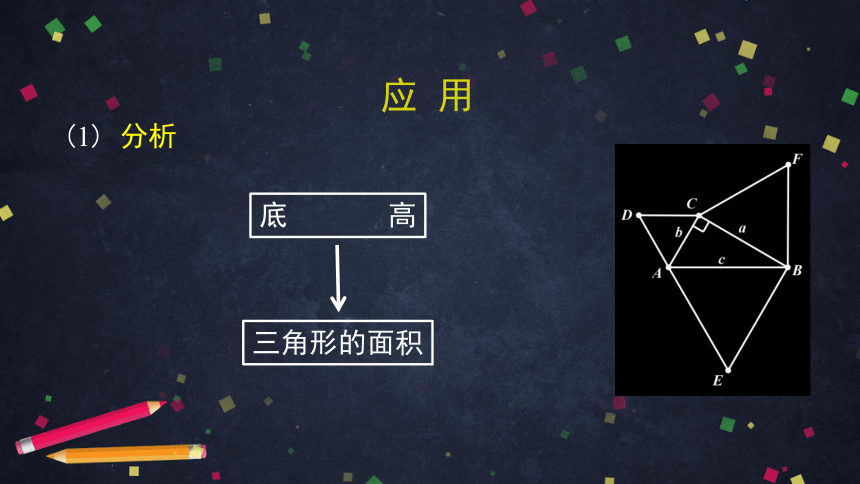
(1) 如果直角三角形的两直角边长分别为a,b,斜边长为c,以直角边a,b为边长的两个等边三角形的面积之和是否等于以斜边c为边长的等边三角形的面积?
应 用
(1) 分析
三角形的面积
底 高
应 用
(1) 解:作 于 .
∵? ABC 是等边三角形,
∴ ,
∴ ,
∵ ,
应 用
(1) 在Rt? AEH中
,
应 用
(1)
,
应 用
(1) 同理可得:
,
,
应 用
(1)
,
∵在Rt?ABC中,
,
.
应 用
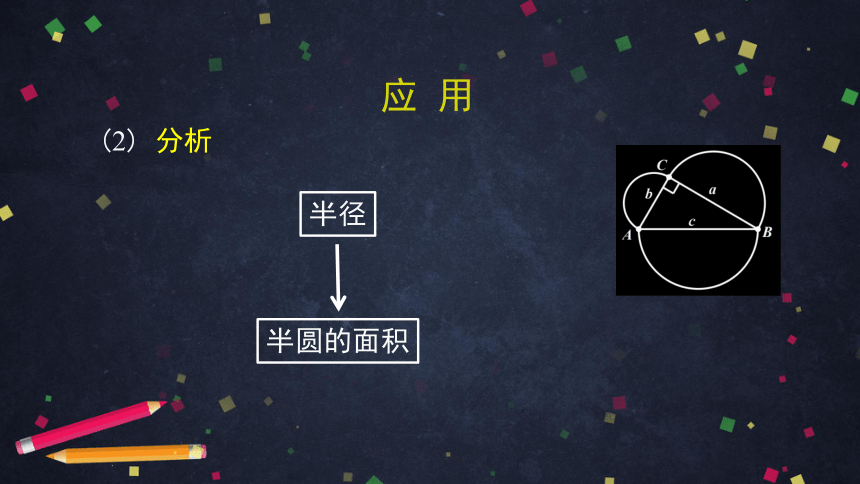
(2) 如果直角三角形的两直角边长分别为a,b,斜边长为c,以直角边a,b为直径的两个半圆的面积之和是否等于以斜边c为直径的半圆的面积?
应 用
(2) 分析
半圆的面积
半径
应 用
,
(2) 解:设以 , , 为直径的半圆面积分别为: , , .
,
,
应 用
(2) ,
∵在Rt?ABC中,
,
.
应 用
例1 反思
,
,
.
应 用
例2 如图,在直线上依次摆放着3个正
方形,水平放置的2个正方形面积分别
为 , , 倾斜放置的正方形面积
为 ,求 , , 之间的关系.
AG,AB,CH
的关系
S1,S2 ,S3
的关系
应 用
例2 分析
BG=CH
?AGB≌?BHC
AB=BC,∠AGB=∠BHC,
∠ABG+∠CBH=∠BCH+∠CBH=90?,
∠ABG=∠BCH,
应 用
例2 证明:∵在正方形EFGA,正方
形ABCD,正方形CHIM中,
∴BG= CH.
∴?AGB≌?BHC,
AB=BC,∠AGB=∠BHC=∠ABC=90?,
∴∠CBH+∠ABG=180?-90?=90?,
∴∠ABG=∠BCH,
∵在Rt?BHC中,∠BCH+∠CBH=90?,
∵∠ABC=90?,
应 用
例2 证明:
∵在Rt?AGB中, ,
∴ ,
.
, , ,
应 用
例2 反思
应 用
例3 (1)如图,这是我国古代著名的
“赵爽弦图”,它由4个全等的直角三
角形和一个小正方形拼接成一个大正
方形,若直角三角形两条直角边分别
为a,b ,大正方形面积为49,
小正方形 面积为4,求 的值.
应 用
例3 (1)分析
解:我们设直角三角形斜边为c,
∴ .
两个正方形的面积
含字母a,b
的等式
应 用
例3 (1)解:由大正方形面积为49 ,
可得: ,也就是 ,
由小正方形面积为4 ,可知小正方形
边长为 ,也就是 ,
∵ ,
∴ ,
∴ ,
应 用
例3 (1)解:
∵ ,
∴ ,
∴ ,
∵ , .
∴
应 用
分析
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
长方形
面积
正方形
面积
正方形
边长
应 用
分析
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
应 用
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
分析
∠ADF=∠BAE,
∠ADF+∠DAF=90?,
∠ADF+∠BAE=90?,
∠DAB=90?,
?ADF ≌ ? BAE,
应 用
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
∠ADC=∠DCB=∠ABC=∠DAB=90?,
分析
AD=DC=CB=BA,
正方形ABCD.
分析
应 用
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
长为2,宽为0.5
的长方形
应 用
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
分析
边长为1的
正方形EFHG
应 用
例3 反思
(1)
赵爽弦图
形
代数式的值
数
应 用
例3 反思
(2)
形
数
应 用
例4 请你在边长为1的正方形网格
纸中,画?ABC,使它的三个顶点
都在格点上,且三边长分别为
AB= ,AC= ,BC= .
应 用
例4 分析:
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
满足条件
应 用
例4 反思
数
形
分类讨论
小 结
几何图形
形
数量关系
数
勾 股 定 理
转 化
分类讨论
作 业
1.如图,分别以在Rt?ABC的三边AC , BC , AB 为直径画半圆,求证:所得两个月形图案AFCD和BGCE的面积和等于Rt△ABC的面积.
作 业
2. 有5个边长为1的正方形,排列形式如图,请把它们分割后拼接成一个大
正方形.
3.?ABC三边长分别为 , ,
,其中 , ,且 ,
请你画出?ABC 并求出它的面积.
祝同学手握思维之匙,
打开数学宝库的大门!
初二年级 数学
勾股定理应用(第二课时)
复习旧知
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么 .
勾股定理
∵在Rt 中,∠C=90°,(已知)
∴ .(勾股定理)
例1. 几何原本中的勾股定理这样表述,如果直角三角形的两直角边长分别
为a,b,斜边长为c,以直角边a,b为边长的两个正方形面积之和等于以斜边c为边长正方形的面积 .
应 用
应 用
(1) 如果直角三角形的两直角边长分别为a,b,斜边长为c,以直角边a,b为边长的两个等边三角形的面积之和是否等于以斜边c为边长的等边三角形的面积?
应 用
(1) 分析
三角形的面积
底 高
应 用
(1) 解:作 于 .
∵? ABC 是等边三角形,
∴ ,
∴ ,
∵ ,
应 用
(1) 在Rt? AEH中
,
应 用
(1)
,
应 用
(1) 同理可得:
,
,
应 用
(1)
,
∵在Rt?ABC中,
,
.
应 用
(2) 如果直角三角形的两直角边长分别为a,b,斜边长为c,以直角边a,b为直径的两个半圆的面积之和是否等于以斜边c为直径的半圆的面积?
应 用
(2) 分析
半圆的面积
半径
应 用
,
(2) 解:设以 , , 为直径的半圆面积分别为: , , .
,
,
应 用
(2) ,
∵在Rt?ABC中,
,
.
应 用
例1 反思
,
,
.
应 用
例2 如图,在直线上依次摆放着3个正
方形,水平放置的2个正方形面积分别
为 , , 倾斜放置的正方形面积
为 ,求 , , 之间的关系.
AG,AB,CH
的关系
S1,S2 ,S3
的关系
应 用
例2 分析
BG=CH
?AGB≌?BHC
AB=BC,∠AGB=∠BHC,
∠ABG+∠CBH=∠BCH+∠CBH=90?,
∠ABG=∠BCH,
应 用
例2 证明:∵在正方形EFGA,正方
形ABCD,正方形CHIM中,
∴BG= CH.
∴?AGB≌?BHC,
AB=BC,∠AGB=∠BHC=∠ABC=90?,
∴∠CBH+∠ABG=180?-90?=90?,
∴∠ABG=∠BCH,
∵在Rt?BHC中,∠BCH+∠CBH=90?,
∵∠ABC=90?,
应 用
例2 证明:
∵在Rt?AGB中, ,
∴ ,
.
, , ,
应 用
例2 反思
应 用
例3 (1)如图,这是我国古代著名的
“赵爽弦图”,它由4个全等的直角三
角形和一个小正方形拼接成一个大正
方形,若直角三角形两条直角边分别
为a,b ,大正方形面积为49,
小正方形 面积为4,求 的值.
应 用
例3 (1)分析
解:我们设直角三角形斜边为c,
∴ .
两个正方形的面积
含字母a,b
的等式
应 用
例3 (1)解:由大正方形面积为49 ,
可得: ,也就是 ,
由小正方形面积为4 ,可知小正方形
边长为 ,也就是 ,
∵ ,
∴ ,
∴ ,
应 用
例3 (1)解:
∵ ,
∴ ,
∴ ,
∵ , .
∴
应 用
分析
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
长方形
面积
正方形
面积
正方形
边长
应 用
分析
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
应 用
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
分析
∠ADF=∠BAE,
∠ADF+∠DAF=90?,
∠ADF+∠BAE=90?,
∠DAB=90?,
?ADF ≌ ? BAE,
应 用
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
∠ADC=∠DCB=∠ABC=∠DAB=90?,
分析
AD=DC=CB=BA,
正方形ABCD.
分析
应 用
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
长为2,宽为0.5
的长方形
应 用
例3 (2)如图,有一个长和宽分别
为6.5和2的长方形,把它分割后拼成
一个大正方形.
分析
边长为1的
正方形EFHG
应 用
例3 反思
(1)
赵爽弦图
形
代数式的值
数
应 用
例3 反思
(2)
形
数
应 用
例4 请你在边长为1的正方形网格
纸中,画?ABC,使它的三个顶点
都在格点上,且三边长分别为
AB= ,AC= ,BC= .
应 用
例4 分析:
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
不满足条件
应 用
例4 分析:
满足条件
应 用
例4 反思
数
形
分类讨论
小 结
几何图形
形
数量关系
数
勾 股 定 理
转 化
分类讨论
作 业
1.如图,分别以在Rt?ABC的三边AC , BC , AB 为直径画半圆,求证:所得两个月形图案AFCD和BGCE的面积和等于Rt△ABC的面积.
作 业
2. 有5个边长为1的正方形,排列形式如图,请把它们分割后拼接成一个大
正方形.
3.?ABC三边长分别为 , ,
,其中 , ,且 ,
请你画出?ABC 并求出它的面积.
祝同学手握思维之匙,
打开数学宝库的大门!
