高中数学人教B版必修三:7.3.2正弦型函数的性质与图像(第三课时) 课件(79张ppt)
文档属性
| 名称 | 高中数学人教B版必修三:7.3.2正弦型函数的性质与图像(第三课时) 课件(79张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 00:00:00 | ||
图片预览








文档简介
(共79张PPT)
高一年级 数学
正弦型函数的性质与图像(第三课时)
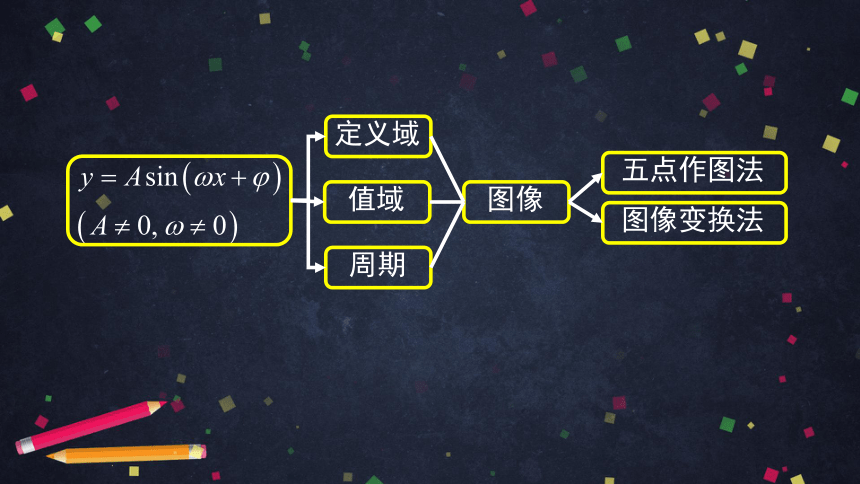
五点作图法
定义域
值域
周期
图像
图像变换法
五点作图法
定义域
值域
周期
图像
图像变换法
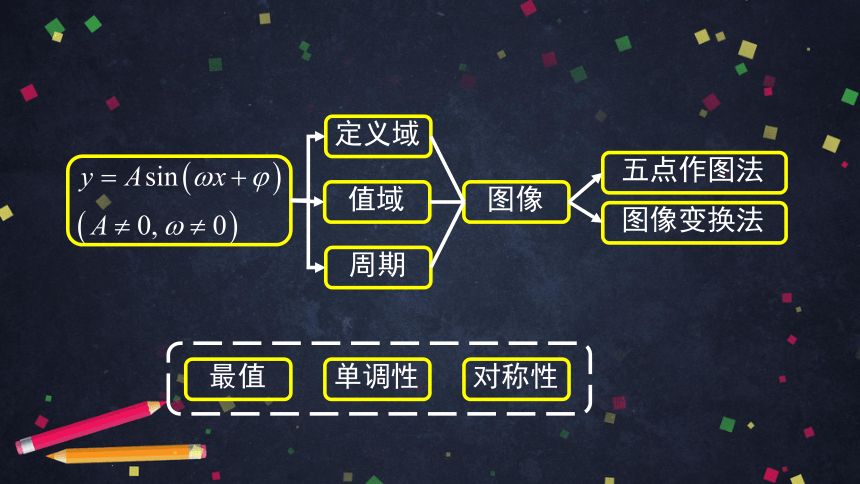
最值
单调性
对称性
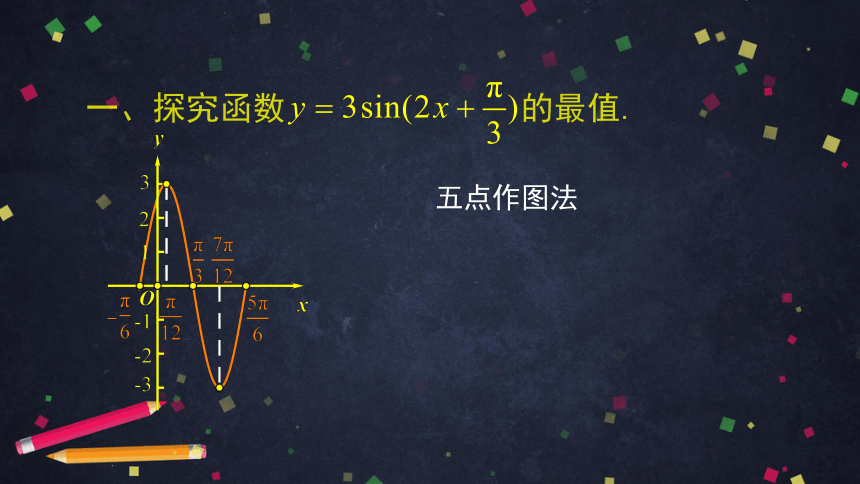
一、探究函数 的最值.
一、探究函数 的最值.
匀速圆周运动
一、探究函数 的最值.
匀速圆周运动
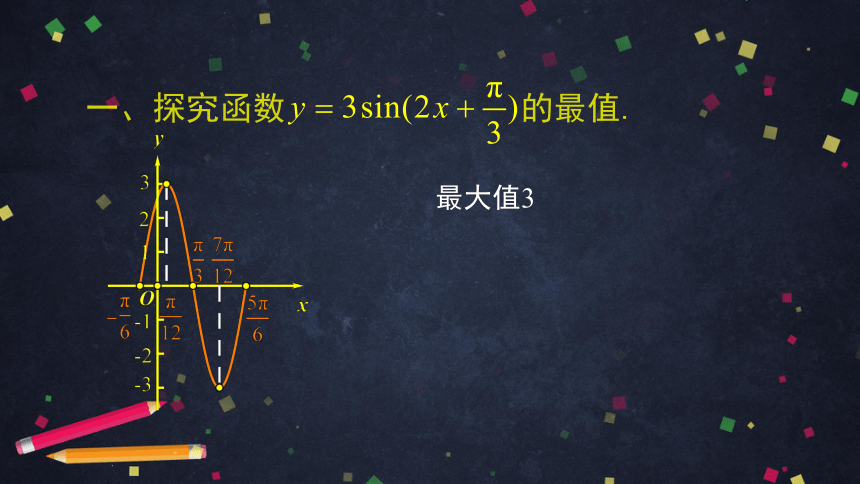
一、探究函数 的最值.
最大值3
一、探究函数 的最值.
最小值-3
五点作图法
一、探究函数 的最值.
最大值3
一、探究函数 的最值.
最大值3
一、探究函数 的最值.
最大值3
一、探究函数 的最值.
最小值-3
一、探究函数 的最值.
图像变换
一、探究函数 的最值.
图像变换
一、探究函数 的最值.
最大值
一、探究函数 的最值.
最大值
一、探究函数 的最值.
最大值
一、探究函数 的最值.
最大值
一、探究函数 的最值.
最小值
一、探究函数 的最值.
一、探究函数 的最值.
换元法
一、探究函数 的最值.
换元法
令 ,
则 时,
取得最大值3.
一、探究函数 的最值.
令 ,则 时,
函数 取得最大值3.
换元法
一、探究函数 的最值.
换元法
令 ,
则 时,
取得最小值-3.
一、探究函数 的最值.
令 ,则 时,
函数 取得最小值-3.
换元法
二、探究函数 的单调性.
匀速圆周运动
二、探究函数 的单调性.
匀速圆周运动
二、探究函数 的单调性.
单调递增
二、探究函数 的单调性.
单调递减
二、探究函数 的单调性.
五点作图法
二、探究函数 的单调性.
单调递减区间
二、探究函数 的单调性.
单调递减区间
二、探究函数 的单调性.
单调递增区间
二、探究函数 的单调性.
图像变换
二、探究函数 的单调性.
单调递增区间
二、探究函数 的单调性.
单调递增区间
二、探究函数 的单调性.
单调递增区间
二、探究函数 的单调性.
单调递减区间
二、探究函数 的单调性.
换元法
令 ,
则 .
函数 单调递增.
二、探究函数 的单调性.
换元法
令 ,
则 .
所以函数 的单调递增区间
为 .
二、探究函数 的单调性.
换元法
令 ,
则 .
函数 单调递减.
二、探究函数 的单调性.
换元法
令 ,
则 .
所以函数 的单调递减区间
为 .
三、探究函数 的对称性.
匀速圆周运动
三、探究函数 的对称性.
对称轴
三、探究函数 的对称性.
对称轴
轴
三、探究函数 的对称性.
对称轴
轴
三、探究函数 的对称性.
对称中心
轴
三、探究函数 的对称性.
五点作图法
三、探究函数 的对称性.
对称轴
三、探究函数 的对称性.
对称中心
三、探究函数 的对称性.
图像变换
三、探究函数 的对称性.
对称轴:
三、探究函数 的对称性.
对称中心:
三、探究函数 的对称性.
换元法
令 ,
则 ,
为函数 的对称轴.
三、探究函数 的对称性.
换元法
令 ,
则 .
所以函数 的对称轴为: .
三、探究函数 的对称性.
换元法
令 ,
则 ,
为函数 的对称中心的横坐标.
三、探究函数 的对称性.
换元法
令 ,
则 .
所以函数 的对称中心为: .
函数 的最值、单调性、对称性之间的联系.
函数 的最值、单调性、对称性之间的联系.
换元法
令 , 研究函数 的性质,进一步得出函数
的性质.
函数 的性质.
最值:
令 ,
当 时,取最大值 .
函数 的性质.
最值:
令 ,
当 时,取最小值 .
单调性:
函数 的性质.
单调增区间:
令 ,
单调性:
函数 的性质.
单调减区间:
令 ,
对称性:
函数 的性质.
对称轴:
令 ,
对称性:
函数 的性质.
对称中心:
令 ,
知识应用
例1、求函数 的单调递增区间.
例1、求函数 的单调递增区间.
解:令 ,
则 .
所以函数 的单调递增区间
为 .
例2、求函数 在区间 上的最大值和最小值.
解:
例2、求函数 在区间 上的最大值和最小值.
例2、求函数 在区间 上的最大值和最小值.
解:
解:
所以当 ,即 时,函数
取得最大值2.
例2、求函数 在区间 上的最大值和最小值.
当 ,即 时,函数
取得最小值-1.
例2、求函数 在区间 上的最大值和最小值.
课堂小结
图像变换
换元法
形
数
单调性
对称性
圆周运动
五点作图
最值
图像变换
换元法
形
数
图像
性质
由特殊到一般
化归与转化
课后作业
1.求 的最大值和最小值,并求出取得最大值和最小值时 的值.
2.求函数 的单调递增区间.
谢谢!
高一年级 数学
正弦型函数的性质与图像(第三课时)
五点作图法
定义域
值域
周期
图像
图像变换法
五点作图法
定义域
值域
周期
图像
图像变换法
最值
单调性
对称性
一、探究函数 的最值.
一、探究函数 的最值.
匀速圆周运动
一、探究函数 的最值.
匀速圆周运动
一、探究函数 的最值.
最大值3
一、探究函数 的最值.
最小值-3
五点作图法
一、探究函数 的最值.
最大值3
一、探究函数 的最值.
最大值3
一、探究函数 的最值.
最大值3
一、探究函数 的最值.
最小值-3
一、探究函数 的最值.
图像变换
一、探究函数 的最值.
图像变换
一、探究函数 的最值.
最大值
一、探究函数 的最值.
最大值
一、探究函数 的最值.
最大值
一、探究函数 的最值.
最大值
一、探究函数 的最值.
最小值
一、探究函数 的最值.
一、探究函数 的最值.
换元法
一、探究函数 的最值.
换元法
令 ,
则 时,
取得最大值3.
一、探究函数 的最值.
令 ,则 时,
函数 取得最大值3.
换元法
一、探究函数 的最值.
换元法
令 ,
则 时,
取得最小值-3.
一、探究函数 的最值.
令 ,则 时,
函数 取得最小值-3.
换元法
二、探究函数 的单调性.
匀速圆周运动
二、探究函数 的单调性.
匀速圆周运动
二、探究函数 的单调性.
单调递增
二、探究函数 的单调性.
单调递减
二、探究函数 的单调性.
五点作图法
二、探究函数 的单调性.
单调递减区间
二、探究函数 的单调性.
单调递减区间
二、探究函数 的单调性.
单调递增区间
二、探究函数 的单调性.
图像变换
二、探究函数 的单调性.
单调递增区间
二、探究函数 的单调性.
单调递增区间
二、探究函数 的单调性.
单调递增区间
二、探究函数 的单调性.
单调递减区间
二、探究函数 的单调性.
换元法
令 ,
则 .
函数 单调递增.
二、探究函数 的单调性.
换元法
令 ,
则 .
所以函数 的单调递增区间
为 .
二、探究函数 的单调性.
换元法
令 ,
则 .
函数 单调递减.
二、探究函数 的单调性.
换元法
令 ,
则 .
所以函数 的单调递减区间
为 .
三、探究函数 的对称性.
匀速圆周运动
三、探究函数 的对称性.
对称轴
三、探究函数 的对称性.
对称轴
轴
三、探究函数 的对称性.
对称轴
轴
三、探究函数 的对称性.
对称中心
轴
三、探究函数 的对称性.
五点作图法
三、探究函数 的对称性.
对称轴
三、探究函数 的对称性.
对称中心
三、探究函数 的对称性.
图像变换
三、探究函数 的对称性.
对称轴:
三、探究函数 的对称性.
对称中心:
三、探究函数 的对称性.
换元法
令 ,
则 ,
为函数 的对称轴.
三、探究函数 的对称性.
换元法
令 ,
则 .
所以函数 的对称轴为: .
三、探究函数 的对称性.
换元法
令 ,
则 ,
为函数 的对称中心的横坐标.
三、探究函数 的对称性.
换元法
令 ,
则 .
所以函数 的对称中心为: .
函数 的最值、单调性、对称性之间的联系.
函数 的最值、单调性、对称性之间的联系.
换元法
令 , 研究函数 的性质,进一步得出函数
的性质.
函数 的性质.
最值:
令 ,
当 时,取最大值 .
函数 的性质.
最值:
令 ,
当 时,取最小值 .
单调性:
函数 的性质.
单调增区间:
令 ,
单调性:
函数 的性质.
单调减区间:
令 ,
对称性:
函数 的性质.
对称轴:
令 ,
对称性:
函数 的性质.
对称中心:
令 ,
知识应用
例1、求函数 的单调递增区间.
例1、求函数 的单调递增区间.
解:令 ,
则 .
所以函数 的单调递增区间
为 .
例2、求函数 在区间 上的最大值和最小值.
解:
例2、求函数 在区间 上的最大值和最小值.
例2、求函数 在区间 上的最大值和最小值.
解:
解:
所以当 ,即 时,函数
取得最大值2.
例2、求函数 在区间 上的最大值和最小值.
当 ,即 时,函数
取得最小值-1.
例2、求函数 在区间 上的最大值和最小值.
课堂小结
图像变换
换元法
形
数
单调性
对称性
圆周运动
五点作图
最值
图像变换
换元法
形
数
图像
性质
由特殊到一般
化归与转化
课后作业
1.求 的最大值和最小值,并求出取得最大值和最小值时 的值.
2.求函数 的单调递增区间.
谢谢!
