人教版六年级下册6.2.2 图形的运动 课件(37张ppt)
文档属性
| 名称 | 人教版六年级下册6.2.2 图形的运动 课件(37张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
图片预览







文档简介
(共37张PPT)
第六单元 整理与复习 2.图形与几何
人教版 数学 六年级下
图形的运动
1.通过整理与复习,进一步巩固我们对轴对称图形、图形
的平移与旋转、图形的放大与缩小的认识,并会按要求
画出指定图形,掌握图形变幻的常用方法。
2.经历动手操作的过程。通过实际操作,产生创造美的欲望。
3.让我们感受几何图形蕴藏的美,激发我们对学习数学的
兴趣。
学习目标:
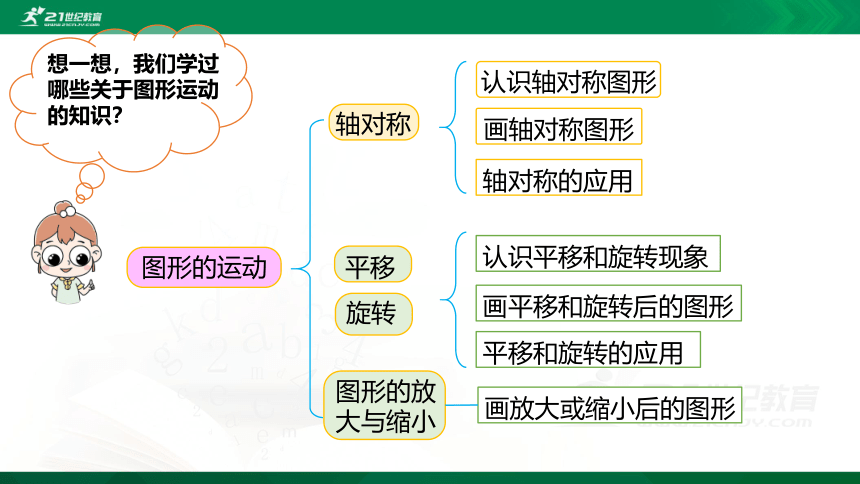
想一想,我们学过哪些关于图形运动的知识?
图形的运动
轴对称
平移
认识轴对称图形
画轴对称图形
轴对称的应用
认识平移和旋转现象
平移和旋转的应用
旋转
图形的放大与缩小
画平移和旋转后的图形
画放大或缩小后的图形
轴对称
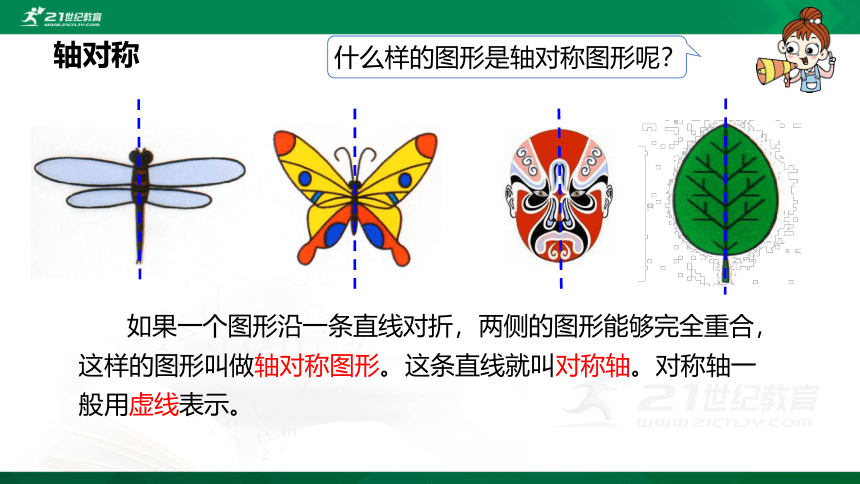
什么样的图形是轴对称图形呢?
如果一个图形沿一条直线对折,两侧的图形能够完全重合, 这样的图形叫做轴对称图形。这条直线就叫对称轴。对称轴一般用虚线表示。
无数条
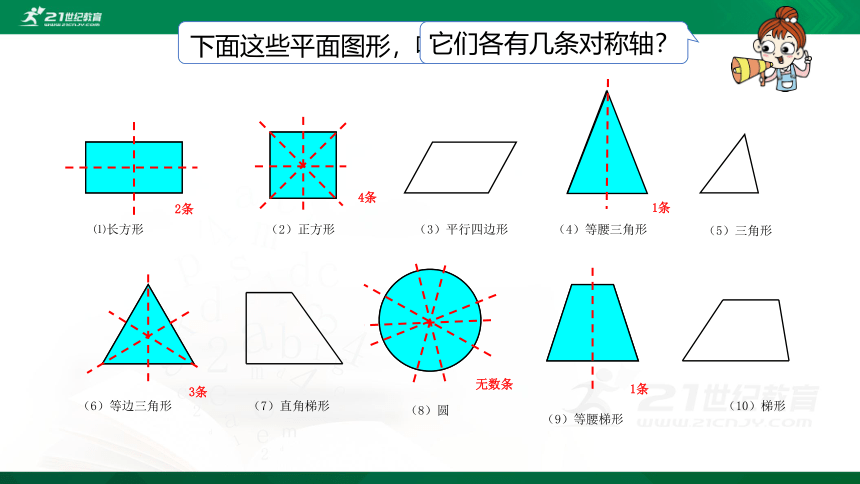
⑴长方形
(2)正方形
(3)平行四边形
(4)等腰三角形
(5)三角形
(6)等边三角形
(7)直角梯形
(8)圆
(9)等腰梯形
(10)梯形
下面这些平面图形,哪些是轴对称图形?
它们各有几条对称轴?
2条
4条
1条
3条
1条
1.下面的图形各是从哪张纸上剪下来的?连一连。
练一练:
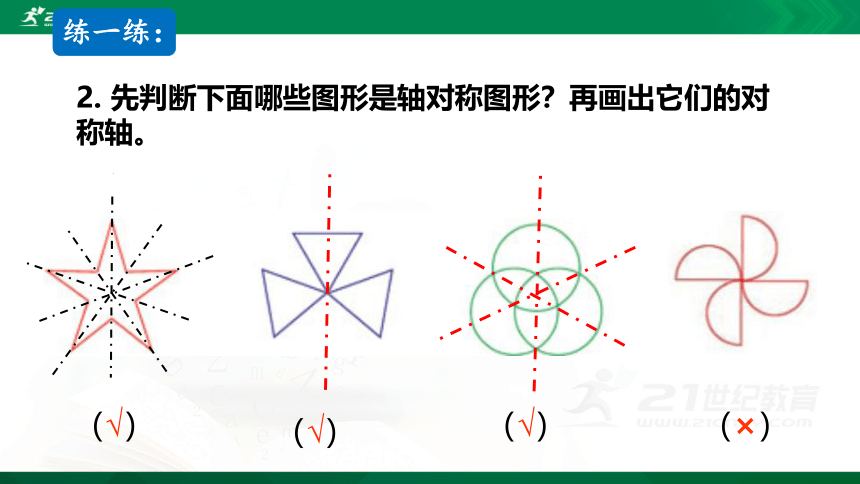
2. 先判断下面哪些图形是轴对称图形?再画出它们的对称轴。
(√)
(×)
(√)
(√)
练一练:
怎样画轴对称图形呢?
找出图形的关键点。
轴对称
B
C
D
B′
C′
·
·
·
D′
E′
·
E
F
每组对应点的连线与对称轴垂直。
轴对称图形中每组对应点到对称轴的距离相等。
A
1
根据对称轴确定每一个端点的对称点。
2
依次连接这些对称点,得到轴对称图形的另一半。
3
利用轴对称特点可以设计精美的图案。
把一个图形沿着某一条直线翻折,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,两个图形中的对应点叫做关于这条直线的对称点,这条直线叫做对称轴。两个图形关于直线对称也称轴对称。
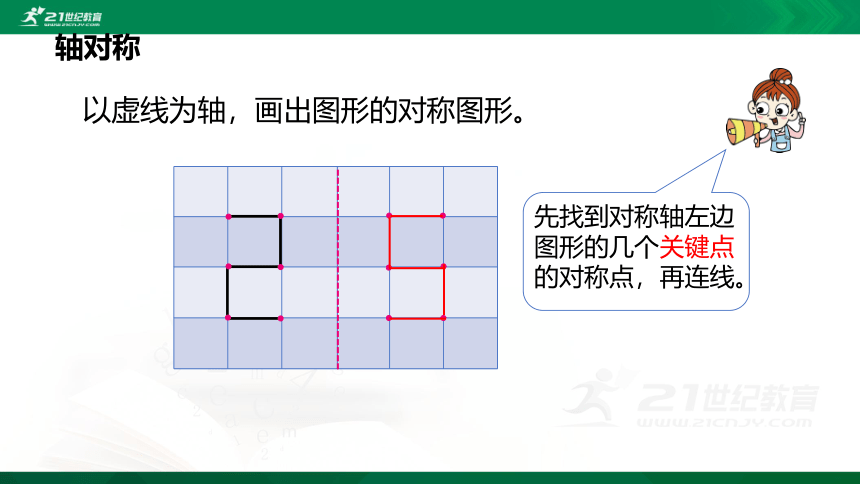
以虚线为轴,画出图形的对称图形。
轴对称
先找到对称轴左边图形的几个关键点的对称点,再连线。
下面哪些现象是平移,哪些现象是旋转?
平移后的图形:大小、方向、形状不变,位置发生变化。
平移:是指在同一平面内,将一个图形上所有点按照某个直线方向做相同距离的移动。这样的图形运动叫做平移。
平移和旋转
如何画平移后的图形?
选点:在原图形上选择关键点。
移点:按要求把关键点向规定的方向平移规定的格数。
最后把这些点顺次连接起来。
旋转:把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称作旋转。
平移和旋转
旋转后的图形:大小和形状不变,位置和方向发生变化。
把一个简单图形旋转一定角度的画法。
第一步:确定所给图形的关键点;
第二步:确定关键点到旋转点的距离;
第三步:确定关键点的对应点;
第四步:把描出的对应点按顺序连线。
注意旋转的方向和角度。
风车绕O点逆时针旋转( )。
O
90°
练一练:
逆时针
风车绕O点逆时针旋转( ) 。
O
180°
练一练:
逆时针
平移与旋转的区别与联系:
联系:都是沿某个方向作运动,运动中都没有改变本身的形状和
大小。都改变了位置。
区别:平移是沿直线运动,旋转在围绕点或轴做圆周运动。
平移不改变自身的方向,旋转改变自身的方向。
画出平移后的图形,再数一数,填一填。
平移和旋转
向上平移5格
向右平移7格
向( )平移( )格
A
·
A′
7格
5格
·
·
左
6
方向
格数
选点平移。
平移和旋转
画出三角形AOB绕点O顺时针旋转90°后的图形。
A
B
O
.
以点O为垂足,在点O右
侧作线段OA的垂线。
线段OA'就是线段OA旋转后的对应线段。
线段OA在方格的竖线上,
它的垂线应在方格的横线上。
以点O为起点,在线段OA的垂线上数出4格。
此点即为点A的对应点A',
A'
B'
同法画出OB旋转后的对应线段OB'。
连接 A′B′。
三角形 A′O B′就是三角形AOB 绕点 O 顺时针旋转 90°后的图形。
轴对称、平移、旋转的应用
利用轴对称、平移、旋转设计美丽图案。
D
C
A
O
B
在生活中轴对称、平移、旋转应用的非常广泛。
图形的放大和缩小
放大或缩小后的图形和原来的图形形状是一样的,只是大小发生了变化。
8cm
5cm
16cm
10cm
长方形B的长是长方形A的长的2倍,宽也是它的2倍。
B与A的长的比是2:1,宽的比是2:1,周长的比是2:1,面积的比是4:1。
A
B
上面长方形按2:1放大,也就是各边( ), 放大后所画的长方形的长要画( )格,宽要画( )格。
怎样画放大后的图形呢?
6
12
3
6
12
6
放大到原来的2倍
先确定扩大的倍数。
再确定扩大后图形的长、宽的格数。
最后画图。
上面长方形按1:3缩小,也就是各边( ), 缩小后所画的长方形的长要画( )格,宽要画( )格。
怎样画缩小后的图形呢?
4
2
12
6
4
2
缩小到原来的三分之一
先确定缩小几分之几。
再确定缩小后图形的长、宽的格数。
最后画图。
1. 下面这些常见的生活现象属于什么运动?
①钟面上分针转动 ②电梯上下运动 ③方向盘转动
④照相 ⑤推拉窗移动 ⑥电风扇转动
⑦投影幻灯 ⑧照镜子 ⑨升国旗
轴对称( ) 平移( )
旋转 ( ) 放大与缩小( )
⑧
①
②
③
④
⑤
⑥
⑦
练一练:
⑨
A→B 向右平移了5格
B→C 先向右平移了5格再绕中心逆时针旋转90度。或者先逆时针旋转90度,再向右平移了5格。
C→D 先向右平移了5格再绕中心逆时针旋转90度。或者先逆时针旋转90度,再向右平移了5格。
练一练:
2.
几 何 乐 园
A
B
图形A向( )平移( )个格,得到图形B。
下
3
A
O B
图形A绕O点按( )方向旋转( )度,再向( )平移( )个格,最后向( )平移( )个格,得到图形B。
顺时针
右
下
1
90
1
俄罗斯方块
1.该怎么移动呢?
(1)图形OABC绕点O逆时针旋转90°,在右图中标出点A的对应点A'。
(2)图形OABC绕点O顺时针旋转( )°,得到图2。
180
乘胜追击
2.我会填!
.
A'
.
.
.
3.请根据给定的对称轴画出图形的另一半。
.
.
.
.
.
① 先找关键点。
②再找对称点。
③连线
思考:放大后的平行四边形的面积与原平行四边形的面积比是( ):( )。
(1)把平行四边形向右平移4格。
(2)把平行四边形按3:1放大。
9
1
●
●
活学活用
4.按要求完成下题。
5. 求阴影部分的面积(单位:厘米)
活学活用
(6+10)×6÷2
=96÷2
=48(cm )
答:阴影部分的面积是48平方厘米。
时
时
9
11
镜面对称的特点:
左右相反
上下不变
镜中的世界
看镜面时间说钟面时间
通过这节课的学习,你有什么收获?
1.通过整理与复习,进一步巩固我们对轴对称图形、图形
的平移与旋转、图形的放大与缩小的认识,并会按要求
画出指定图形,掌握图形变幻的常用方法。
2.经历动手操作的过程。通过实际操作,产生创造美的欲望。
3.让我们感受几何图形蕴藏的美,激发我们对学习数学的
兴趣。
学习目标:
你完成今天的学习目标了吗?
图形的运动
轴对称
平移
认识轴对称图形
画轴对称图形
轴对称的应用
认识平移和旋转现象
平移和旋转的应用
旋转
图形的放大与缩小
画平移和旋转后的图形
画放大或缩小后的图形
1.平移、旋转和轴对称不改变图形的形状和大小;
3.图形的放大和缩小只改变大小,不改变形状。
①先确定扩大或缩小的比。
②再确定格数。
③画图。
2.作图步骤:
4.作图步骤:
① 先找关键点。
②再找对称点。
③连线。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第六单元 整理与复习 2.图形与几何
人教版 数学 六年级下
图形的运动
1.通过整理与复习,进一步巩固我们对轴对称图形、图形
的平移与旋转、图形的放大与缩小的认识,并会按要求
画出指定图形,掌握图形变幻的常用方法。
2.经历动手操作的过程。通过实际操作,产生创造美的欲望。
3.让我们感受几何图形蕴藏的美,激发我们对学习数学的
兴趣。
学习目标:
想一想,我们学过哪些关于图形运动的知识?
图形的运动
轴对称
平移
认识轴对称图形
画轴对称图形
轴对称的应用
认识平移和旋转现象
平移和旋转的应用
旋转
图形的放大与缩小
画平移和旋转后的图形
画放大或缩小后的图形
轴对称
什么样的图形是轴对称图形呢?
如果一个图形沿一条直线对折,两侧的图形能够完全重合, 这样的图形叫做轴对称图形。这条直线就叫对称轴。对称轴一般用虚线表示。
无数条
⑴长方形
(2)正方形
(3)平行四边形
(4)等腰三角形
(5)三角形
(6)等边三角形
(7)直角梯形
(8)圆
(9)等腰梯形
(10)梯形
下面这些平面图形,哪些是轴对称图形?
它们各有几条对称轴?
2条
4条
1条
3条
1条
1.下面的图形各是从哪张纸上剪下来的?连一连。
练一练:
2. 先判断下面哪些图形是轴对称图形?再画出它们的对称轴。
(√)
(×)
(√)
(√)
练一练:
怎样画轴对称图形呢?
找出图形的关键点。
轴对称
B
C
D
B′
C′
·
·
·
D′
E′
·
E
F
每组对应点的连线与对称轴垂直。
轴对称图形中每组对应点到对称轴的距离相等。
A
1
根据对称轴确定每一个端点的对称点。
2
依次连接这些对称点,得到轴对称图形的另一半。
3
利用轴对称特点可以设计精美的图案。
把一个图形沿着某一条直线翻折,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,两个图形中的对应点叫做关于这条直线的对称点,这条直线叫做对称轴。两个图形关于直线对称也称轴对称。
以虚线为轴,画出图形的对称图形。
轴对称
先找到对称轴左边图形的几个关键点的对称点,再连线。
下面哪些现象是平移,哪些现象是旋转?
平移后的图形:大小、方向、形状不变,位置发生变化。
平移:是指在同一平面内,将一个图形上所有点按照某个直线方向做相同距离的移动。这样的图形运动叫做平移。
平移和旋转
如何画平移后的图形?
选点:在原图形上选择关键点。
移点:按要求把关键点向规定的方向平移规定的格数。
最后把这些点顺次连接起来。
旋转:把一个图形围绕某一固定点按顺时针或逆时针方向转动一定的角度的过程,称作旋转。
平移和旋转
旋转后的图形:大小和形状不变,位置和方向发生变化。
把一个简单图形旋转一定角度的画法。
第一步:确定所给图形的关键点;
第二步:确定关键点到旋转点的距离;
第三步:确定关键点的对应点;
第四步:把描出的对应点按顺序连线。
注意旋转的方向和角度。
风车绕O点逆时针旋转( )。
O
90°
练一练:
逆时针
风车绕O点逆时针旋转( ) 。
O
180°
练一练:
逆时针
平移与旋转的区别与联系:
联系:都是沿某个方向作运动,运动中都没有改变本身的形状和
大小。都改变了位置。
区别:平移是沿直线运动,旋转在围绕点或轴做圆周运动。
平移不改变自身的方向,旋转改变自身的方向。
画出平移后的图形,再数一数,填一填。
平移和旋转
向上平移5格
向右平移7格
向( )平移( )格
A
·
A′
7格
5格
·
·
左
6
方向
格数
选点平移。
平移和旋转
画出三角形AOB绕点O顺时针旋转90°后的图形。
A
B
O
.
以点O为垂足,在点O右
侧作线段OA的垂线。
线段OA'就是线段OA旋转后的对应线段。
线段OA在方格的竖线上,
它的垂线应在方格的横线上。
以点O为起点,在线段OA的垂线上数出4格。
此点即为点A的对应点A',
A'
B'
同法画出OB旋转后的对应线段OB'。
连接 A′B′。
三角形 A′O B′就是三角形AOB 绕点 O 顺时针旋转 90°后的图形。
轴对称、平移、旋转的应用
利用轴对称、平移、旋转设计美丽图案。
D
C
A
O
B
在生活中轴对称、平移、旋转应用的非常广泛。
图形的放大和缩小
放大或缩小后的图形和原来的图形形状是一样的,只是大小发生了变化。
8cm
5cm
16cm
10cm
长方形B的长是长方形A的长的2倍,宽也是它的2倍。
B与A的长的比是2:1,宽的比是2:1,周长的比是2:1,面积的比是4:1。
A
B
上面长方形按2:1放大,也就是各边( ), 放大后所画的长方形的长要画( )格,宽要画( )格。
怎样画放大后的图形呢?
6
12
3
6
12
6
放大到原来的2倍
先确定扩大的倍数。
再确定扩大后图形的长、宽的格数。
最后画图。
上面长方形按1:3缩小,也就是各边( ), 缩小后所画的长方形的长要画( )格,宽要画( )格。
怎样画缩小后的图形呢?
4
2
12
6
4
2
缩小到原来的三分之一
先确定缩小几分之几。
再确定缩小后图形的长、宽的格数。
最后画图。
1. 下面这些常见的生活现象属于什么运动?
①钟面上分针转动 ②电梯上下运动 ③方向盘转动
④照相 ⑤推拉窗移动 ⑥电风扇转动
⑦投影幻灯 ⑧照镜子 ⑨升国旗
轴对称( ) 平移( )
旋转 ( ) 放大与缩小( )
⑧
①
②
③
④
⑤
⑥
⑦
练一练:
⑨
A→B 向右平移了5格
B→C 先向右平移了5格再绕中心逆时针旋转90度。或者先逆时针旋转90度,再向右平移了5格。
C→D 先向右平移了5格再绕中心逆时针旋转90度。或者先逆时针旋转90度,再向右平移了5格。
练一练:
2.
几 何 乐 园
A
B
图形A向( )平移( )个格,得到图形B。
下
3
A
O B
图形A绕O点按( )方向旋转( )度,再向( )平移( )个格,最后向( )平移( )个格,得到图形B。
顺时针
右
下
1
90
1
俄罗斯方块
1.该怎么移动呢?
(1)图形OABC绕点O逆时针旋转90°,在右图中标出点A的对应点A'。
(2)图形OABC绕点O顺时针旋转( )°,得到图2。
180
乘胜追击
2.我会填!
.
A'
.
.
.
3.请根据给定的对称轴画出图形的另一半。
.
.
.
.
.
① 先找关键点。
②再找对称点。
③连线
思考:放大后的平行四边形的面积与原平行四边形的面积比是( ):( )。
(1)把平行四边形向右平移4格。
(2)把平行四边形按3:1放大。
9
1
●
●
活学活用
4.按要求完成下题。
5. 求阴影部分的面积(单位:厘米)
活学活用
(6+10)×6÷2
=96÷2
=48(cm )
答:阴影部分的面积是48平方厘米。
时
时
9
11
镜面对称的特点:
左右相反
上下不变
镜中的世界
看镜面时间说钟面时间
通过这节课的学习,你有什么收获?
1.通过整理与复习,进一步巩固我们对轴对称图形、图形
的平移与旋转、图形的放大与缩小的认识,并会按要求
画出指定图形,掌握图形变幻的常用方法。
2.经历动手操作的过程。通过实际操作,产生创造美的欲望。
3.让我们感受几何图形蕴藏的美,激发我们对学习数学的
兴趣。
学习目标:
你完成今天的学习目标了吗?
图形的运动
轴对称
平移
认识轴对称图形
画轴对称图形
轴对称的应用
认识平移和旋转现象
平移和旋转的应用
旋转
图形的放大与缩小
画平移和旋转后的图形
画放大或缩小后的图形
1.平移、旋转和轴对称不改变图形的形状和大小;
3.图形的放大和缩小只改变大小,不改变形状。
①先确定扩大或缩小的比。
②再确定格数。
③画图。
2.作图步骤:
4.作图步骤:
① 先找关键点。
②再找对称点。
③连线。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
