人教版数学八年级下册 17.1 勾股定理同步练习含答案
文档属性
| 名称 | 人教版数学八年级下册 17.1 勾股定理同步练习含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 716.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
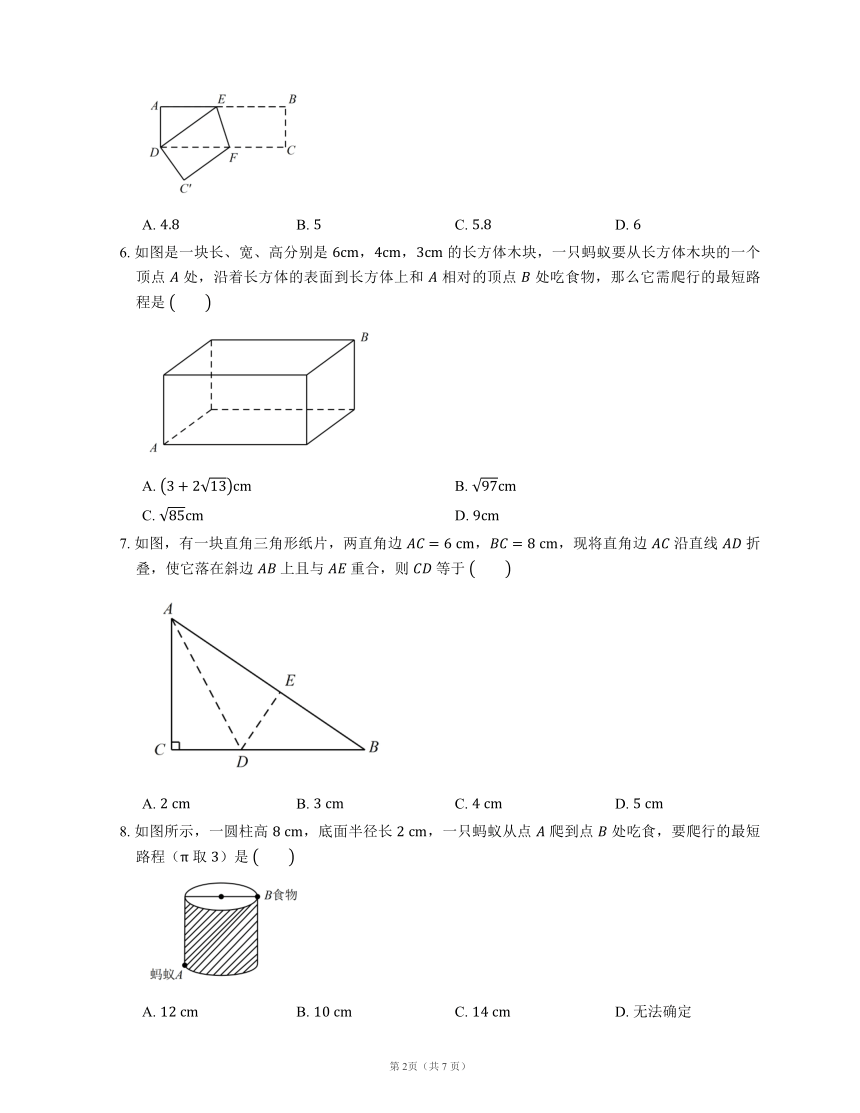
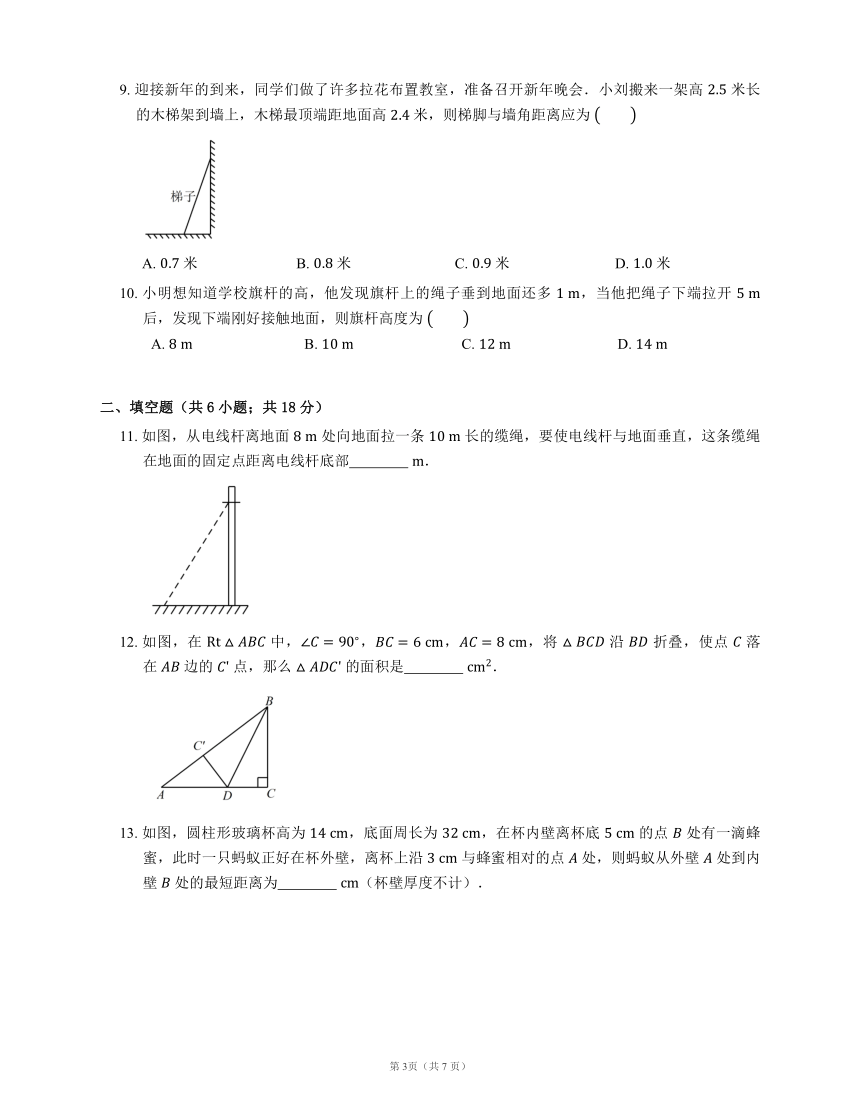
图片预览

文档简介
17.1 勾股定理
总分:100分
班级:__________ 姓名:__________ 学号:__________ 得分:__________
一、选择题(共10小题;共30分)
1. 如图,小巷左右两侧是竖着的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 米,顶端距离地面 米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面 米.则小巷的宽度为
A. 米 B. 米 C. 米 D. 米
2. 如图,一只蚂蚁从长、宽都是 ,高是 的长方体纸箱的 点沿纸箱爬到 点,那么它爬行的最短路线的长是
A. B. C. D.
3. 如图所示,有一块直角三角形纸片,两直角边分别为 ,,现将直角边 沿直线 折叠,使它落在斜边 上,且与 重合,则 等于
A. B. C. D.
4. 小强量得家里新购置的彩电荧光屏的长为 ,宽为 ,则这台电视机的尺寸(屏幕的对角线长度为电视机的尺寸)最有可能是
A. 英寸 B. 英寸
C. 英寸 D. 英寸
5. 如图,长方形纸片 中,,,按如图的方式折叠,使点 与点 重合.折痕为 ,则 长为 .
A. B. C. D.
6. 如图是一块长、宽、高分别是 ,, 的长方体木块,一只蚂蚁要从长方体木块的一个顶点 处,沿着长方体的表面到长方体上和 相对的顶点 处吃食物,那么它需爬行的最短路程是
A. B.
C. D.
7. 如图,有一块直角三角形纸片,两直角边 ,,现将直角边 沿直线 折叠,使它落在斜边 上且与 重合,则 等于
A. B. C. D.
8. 如图所示,一圆柱高 ,底面半径长 ,一只蚂蚁从点 爬到点 处吃食,要爬行的最短路程( 取 )是
A. B. C. D. 无法确定
9. 迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会.小刘搬来一架高 米长的木梯架到墙上,木梯最顶端距地面高 米,则梯脚与墙角距离应为
A. 米 B. 米 C. 米 D. 米
10. 小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多 ,当他把绳子下端拉开 后,发现下端刚好接触地面,则旗杆高度为
A. B. C. D.
二、填空题(共6小题;共18分)
11. 如图,从电线杆离地面 处向地面拉一条 长的缆绳,要使电线杆与地面垂直,这条缆绳在地面的固定点距离电线杆底部 ? .
12. 如图,在 中,,,,将 沿 折叠,使点 落在 边的 点,那么 的面积是 ? .
13. 如图,圆柱形玻璃杯高为 ,底面周长为 ,在杯内壁离杯底 的点 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的点 处,则蚂蚁从外壁 处到内壁 处的最短距离为 ? (杯壁厚度不计).
14. 木工周师傅加工一个长方形桌面,测量得到桌面的长为 ,宽为 ,对角线长为 ,这个桌面 ?(填“合格”或“不合格”).
15. 如图,有一块直角三角形纸片,两直角边 ,,现直角边沿直线 折叠,使它落在斜边 上,且与 重合,则 的长为 ?.
16. 如图,长方体的底面边长分别为 和 ,高为 ,若一只蚂蚁从 点开始经过 个侧面爬行一圈到达 点,则蚂蚁爬行的最短路径长为 ? .
三、解答题(共6小题;共52分)
17. 如图所示,某人到一个荒岛上去探宝,在 处登陆后,往东走 ,又往北走 ,遇到障碍后又往西走 ,再折向北走 后往东拐仅走 就找到了宝藏.登录点( 处)到宝藏埋藏点( 处)的直线距离是多少?
18. 如图,在 中,,,,按图中所示方法将 沿 折叠,使点 落在 边的 点.
(1)求 的长;
(2)求 的面积.
19. 如图,圆柱的高为 ,底面直径 ,在圆柱下底面的 点有一只蚂蚁,它想吃到上底面上与 点相对的 点处的食物,它需要爬行的最短路程是多少厘米?
20. 已知,如图所示,折叠长方形的一边 ,使点 落在 边的点 处,如果 ,.求 的长.
21. 葛藤是一种植物,它自己腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一个绝招,就是它绕树盘升的路线,总是沿最短路线螺旋前进的.
(1)如果树的周长为 ,绕一圈升高 ,则它爬行路程是多少?
(2)如果树的周长为 ,绕一圈爬行 ,则爬行一圈升高多少 ?如果爬行 圈到达树顶,则树干多高?
22. 如图, 城气象台测得台风中心在 城正西方向 的 处,以每小时 的速度向北偏东 的 方向移动,距离台风中心 的范围内是受台风影响的区域.
(1) 城是否受到这次台风影响?为什么?
(2)若 城受到这次台风影响,那么 城遭受这次台风影响有多长时间?
答案
第一部分
1. C
2. A
3. B
4. C
5. C
6. C 【解析】将长方体表面展开后,由两点之间线段最短,可得有三种可能的行走方式,路程分别为:,,,
所以最短路程为 .
7. B
8. B
9. A
10. C
第二部分
11.
12.
13.
14. 合格
15.
16.
【解析】要求长方体中两点之间的最短路径,最直接的做法就是将长方体展开,然后利用两点之间线段最短解答.
如图
,, ,
第三部分
17.
18. (1) ,,,
,
由翻折变换的性质得,,,,
,,
设 ,则 ,,
在 中,由勾股定理得,,
即 ,
解得 ,
即 .
??????(2) ,
.
19. 解:将此圆柱展成平面图得:
∵有一圆柱,它的高等于 ,底面直径等于 ,
∴ ,,
∴ .
答:它需要爬行的最短路程约为 .
20.
21. (1)
??????(2) ;
22. (1) 城受台风影响.
理由:
应过点 作 ,垂足为 .
,,,
.
,
城会受到这次台风影响.
??????(2) 小时.
第1页(共1 页)
总分:100分
班级:__________ 姓名:__________ 学号:__________ 得分:__________
一、选择题(共10小题;共30分)
1. 如图,小巷左右两侧是竖着的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为 米,顶端距离地面 米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面 米.则小巷的宽度为
A. 米 B. 米 C. 米 D. 米
2. 如图,一只蚂蚁从长、宽都是 ,高是 的长方体纸箱的 点沿纸箱爬到 点,那么它爬行的最短路线的长是
A. B. C. D.
3. 如图所示,有一块直角三角形纸片,两直角边分别为 ,,现将直角边 沿直线 折叠,使它落在斜边 上,且与 重合,则 等于
A. B. C. D.
4. 小强量得家里新购置的彩电荧光屏的长为 ,宽为 ,则这台电视机的尺寸(屏幕的对角线长度为电视机的尺寸)最有可能是
A. 英寸 B. 英寸
C. 英寸 D. 英寸
5. 如图,长方形纸片 中,,,按如图的方式折叠,使点 与点 重合.折痕为 ,则 长为 .
A. B. C. D.
6. 如图是一块长、宽、高分别是 ,, 的长方体木块,一只蚂蚁要从长方体木块的一个顶点 处,沿着长方体的表面到长方体上和 相对的顶点 处吃食物,那么它需爬行的最短路程是
A. B.
C. D.
7. 如图,有一块直角三角形纸片,两直角边 ,,现将直角边 沿直线 折叠,使它落在斜边 上且与 重合,则 等于
A. B. C. D.
8. 如图所示,一圆柱高 ,底面半径长 ,一只蚂蚁从点 爬到点 处吃食,要爬行的最短路程( 取 )是
A. B. C. D. 无法确定
9. 迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会.小刘搬来一架高 米长的木梯架到墙上,木梯最顶端距地面高 米,则梯脚与墙角距离应为
A. 米 B. 米 C. 米 D. 米
10. 小明想知道学校旗杆的高,他发现旗杆上的绳子垂到地面还多 ,当他把绳子下端拉开 后,发现下端刚好接触地面,则旗杆高度为
A. B. C. D.
二、填空题(共6小题;共18分)
11. 如图,从电线杆离地面 处向地面拉一条 长的缆绳,要使电线杆与地面垂直,这条缆绳在地面的固定点距离电线杆底部 ? .
12. 如图,在 中,,,,将 沿 折叠,使点 落在 边的 点,那么 的面积是 ? .
13. 如图,圆柱形玻璃杯高为 ,底面周长为 ,在杯内壁离杯底 的点 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 与蜂蜜相对的点 处,则蚂蚁从外壁 处到内壁 处的最短距离为 ? (杯壁厚度不计).
14. 木工周师傅加工一个长方形桌面,测量得到桌面的长为 ,宽为 ,对角线长为 ,这个桌面 ?(填“合格”或“不合格”).
15. 如图,有一块直角三角形纸片,两直角边 ,,现直角边沿直线 折叠,使它落在斜边 上,且与 重合,则 的长为 ?.
16. 如图,长方体的底面边长分别为 和 ,高为 ,若一只蚂蚁从 点开始经过 个侧面爬行一圈到达 点,则蚂蚁爬行的最短路径长为 ? .
三、解答题(共6小题;共52分)
17. 如图所示,某人到一个荒岛上去探宝,在 处登陆后,往东走 ,又往北走 ,遇到障碍后又往西走 ,再折向北走 后往东拐仅走 就找到了宝藏.登录点( 处)到宝藏埋藏点( 处)的直线距离是多少?
18. 如图,在 中,,,,按图中所示方法将 沿 折叠,使点 落在 边的 点.
(1)求 的长;
(2)求 的面积.
19. 如图,圆柱的高为 ,底面直径 ,在圆柱下底面的 点有一只蚂蚁,它想吃到上底面上与 点相对的 点处的食物,它需要爬行的最短路程是多少厘米?
20. 已知,如图所示,折叠长方形的一边 ,使点 落在 边的点 处,如果 ,.求 的长.
21. 葛藤是一种植物,它自己腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一个绝招,就是它绕树盘升的路线,总是沿最短路线螺旋前进的.
(1)如果树的周长为 ,绕一圈升高 ,则它爬行路程是多少?
(2)如果树的周长为 ,绕一圈爬行 ,则爬行一圈升高多少 ?如果爬行 圈到达树顶,则树干多高?
22. 如图, 城气象台测得台风中心在 城正西方向 的 处,以每小时 的速度向北偏东 的 方向移动,距离台风中心 的范围内是受台风影响的区域.
(1) 城是否受到这次台风影响?为什么?
(2)若 城受到这次台风影响,那么 城遭受这次台风影响有多长时间?
答案
第一部分
1. C
2. A
3. B
4. C
5. C
6. C 【解析】将长方体表面展开后,由两点之间线段最短,可得有三种可能的行走方式,路程分别为:,,,
所以最短路程为 .
7. B
8. B
9. A
10. C
第二部分
11.
12.
13.
14. 合格
15.
16.
【解析】要求长方体中两点之间的最短路径,最直接的做法就是将长方体展开,然后利用两点之间线段最短解答.
如图
,, ,
第三部分
17.
18. (1) ,,,
,
由翻折变换的性质得,,,,
,,
设 ,则 ,,
在 中,由勾股定理得,,
即 ,
解得 ,
即 .
??????(2) ,
.
19. 解:将此圆柱展成平面图得:
∵有一圆柱,它的高等于 ,底面直径等于 ,
∴ ,,
∴ .
答:它需要爬行的最短路程约为 .
20.
21. (1)
??????(2) ;
22. (1) 城受台风影响.
理由:
应过点 作 ,垂足为 .
,,,
.
,
城会受到这次台风影响.
??????(2) 小时.
第1页(共1 页)
