人教版数学八年级下册 19.3 课题学习 选择方案同步测试含答案
文档属性
| 名称 | 人教版数学八年级下册 19.3 课题学习 选择方案同步测试含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 765.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 10:30:52 | ||
图片预览




文档简介
19.3 课题学习 选择方案
总分:100分
班级:__________ 姓名:__________ 学号:__________ 得分:__________
一、选择题(共10小题;共30分)
1. 平面直角坐标系内 轴,,点 的坐标为 ,则点 的坐标为
A. B.
C. 或 D. 或
2. 小敏从 A 地出发向 B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点 的两条线段 , 分别表示小敏、小聪离B地的距离 与已用时间 之间的关系,则小敏、小聪行走的速度分别是
A. 和 B. 和
C. 和 D. 和
3. 实数 在数轴上对应的点如图所示,则 的大小关系正确的是 .
A. B. C. D.
4. 若等腰三角形中的一个外角等于 ,则它的顶角的度数是
A. B. C. D. 或
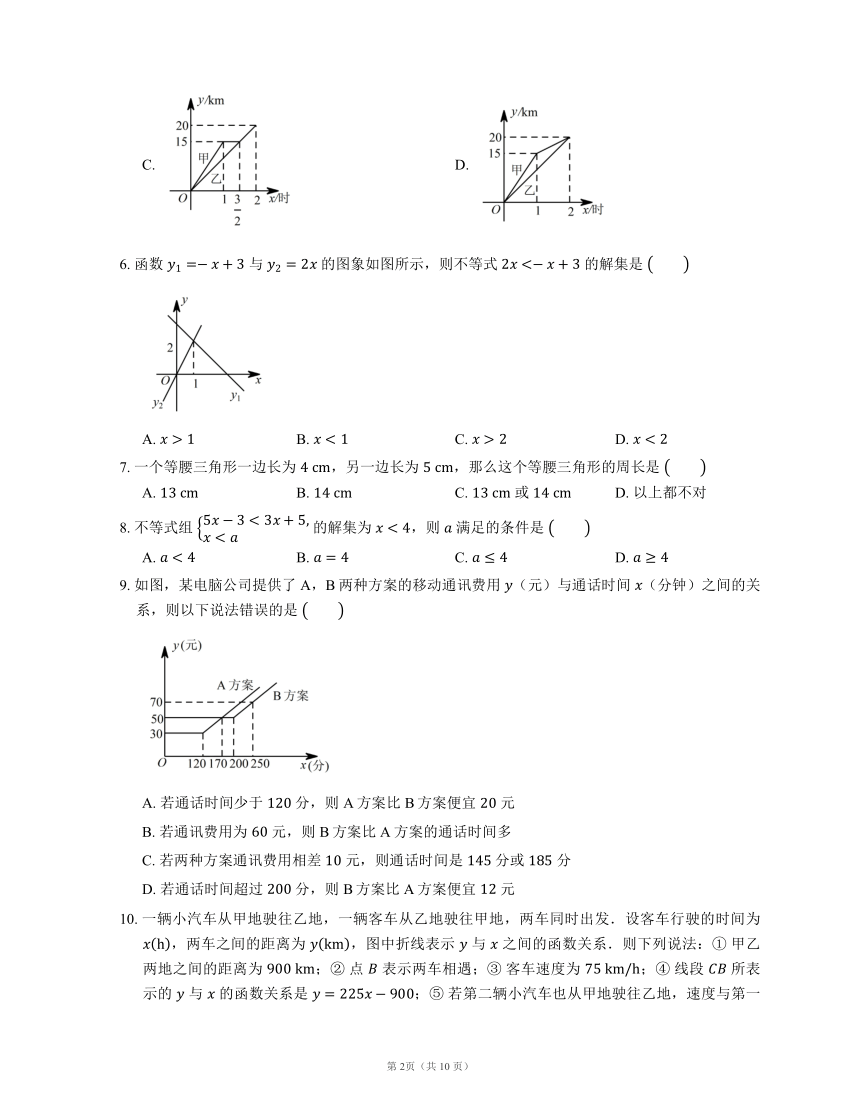
5. 一段笔直的公路 长 千米,途中有一处休息点 , 长 千米.甲、乙两名长跑爱好者同时从点 出发.甲以 千米/时的速度匀速跑至点 ,原地休息半小时后,再以 千米/时的速度匀速跑至终点 ;乙以 千米/时的速度匀速跑至终点 .下列选项中,能正确反映甲、乙两人出发后 小时内运动路程 (千米)与时间 (小时)函数关系的图象是
A. B.
C. D.
6. 函数 与 的图象如图所示,则不等式 的解集是
A. B. C. D.
7. 一个等腰三角形一边长为 ,另一边长为 ,那么这个等腰三角形的周长是
A. B. C. 或 D. 以上都不对
8. 不等式组 的解集为 ,则 满足的条件是
A. B. C. D.
9. 如图,某电脑公司提供了A,B两种方案的移动通讯费用 (元)与通话时间 (分钟)之间的关系,则以下说法错误的是
A. 若通话时间少于 分,则A方案比B方案便宜 元
B. 若通讯费用为 元,则B方案比A方案的通话时间多
C. 若两种方案通讯费用相差 元,则通话时间是 分或 分
D. 若通话时间超过 分,则B方案比A方案便宜 元
10. 一辆小汽车从甲地驶往乙地,一辆客车从乙地驶往甲地,两车同时出发.设客车行驶的时间为 ,两车之间的距离为 ,图中折线表示 与 之间的函数关系.则下列说法:① 甲乙两地之间的距离为 ;② 点 表示两车相遇;③ 客车速度为 ;④ 线段 所表示的 与 的函数关系是 ;⑤ 若第二辆小汽车也从甲地驶往乙地,速度与第一辆小汽车相同.在第一辆小汽车与客车相遇 分钟后,第二辆小汽车与客车相遇,则第二辆小汽车比第一辆小汽车晚出发 .其中正确的有
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题;共18分)
11. 已知等腰三角形的周长为 ,设它的腰长为 ,底边长为 ,则 与 的函数关系式是 ?;其中自变量是 ?.
12. 张老师带领 名学生到某动物园参观,已知成人票每张 元,学生票每张 元,设门票的总费用为 元,则 ?;其中自变量是 ?,自变量的函数是 ?.
13. 如果直角三角形的三边长为 ,,,则最短边上的高为 ?.
14. 如图,一次函数 的图象经过 , 两点,则 解集是 ?.
15. 如图,已知一次函数 与一次函数 的图象相交于点 ,则不等式 的解集是 ?.
16. 已知线段 平行于 轴,且 的长度为 ,若 ,则点 的坐标 ?.
三、解答题(共6小题;共52分)
17. (1)求过点 且与已知直线 平行的直线 的函数表达式,并画出直线 的图象;
(2)设直线 分别与 轴、 轴交于点 、点 ,如果直线 与直线 平行且交 轴于点 ,求出 的面积 关于 的函数表达式.
18. 已知一次函数的图象与正比例函数 的图象平行,且经过点 .
(1)求一次函数的解析式.
(2)若点 和 在一次函数的图象上,求 , 的值.
19. 甲、乙两辆汽车沿同一路线赶赴距出发地 千米的目的地,乙车比甲车晚出发 小时(从甲车出发时开始计时),图中折线 ,线段 分别表示甲、乙两车所行路程 (千米)与时间 (小时)之间的函数关系对应的图象(线段 表示甲出发不足 小时因故停车检修),请根据图象所提供的信息,解决如下问题:
(1)求乙车所行路程 与时间 的函数关系式;
(2)乙车出发多长时间,两车在途中第一次相遇?(要写出解题过程)
20. 如图,在平面直角坐标系中,直线 与直线 交点 的横坐标为 ,将直线 沿 轴向下平移 个单位长度,得到直线 ,直线 与 轴交于点 ,与直线 交于点 ,点 的纵坐标为 ,直线 与 轴交于点 .
(1)求直线 的解析式;
(2)求 的面积.
21. 某公司在甲、乙仓库共存放某种原料 吨,如果运出甲仓库所存原料的 ,乙仓库所存原料的 ,那么乙仓库剩余的原料比甲仓库剩余的原料多 吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将 吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为 元/吨和 元/吨.经协商,从甲仓库到工厂的运价可优惠 元/吨 ,从乙仓库到工厂的运价不变,设从甲仓库运 吨原料到工厂,请求出总运费 关于 的函数解析式(不要求写出 的取值范围);
(3)在()的条件下,请根据函数的性质说明:随着 的增大, 的变化情况.
22. 新农村社区改造中,有一部分楼盘要对外销售.某楼盘共 层,销售价格如下:第八层楼房售价为 元/平方米,从第八层起每上升一层,每平方米的售价提高 元;反之,楼层每下降一层,每平方米的售价降低 元,已知该楼盘每套楼房面积均为 平方米.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价 ,另外每套楼房赠送 元装修基金;
方案二:降价 ,没有其他赠送.
(1)请写出售价 (元/平方米)与楼层 之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
答案
第一部分
1. C
2. D
3. D
4. D
5. A
【解析】本题考查一次函数图象的实际应用.甲匀速跑至 点用时 小时 ,原地休息半小时此时 ,再以 千米/时的速度匀速跑至终点 ,
千米, 千米,
千米,
甲从 至 还需 小时,
甲跑 段 ;乙跑 千米/时的速度匀速跑到点 ,则 ,当 时,.
6. B
7. C 【解析】当 为等腰三角形的腰时,
三角形的三边分别是 ,, 符合三角形的三边关系,
周长为 ;
当 为等腰三角形的腰时,
三边分别是 ,,,符合三角形的三边关系,
周长为 .
8. D 【解析】解不等式组得:
不等式组 的解 ,
.
9. C 【解析】设 时A方案的移动通讯费用与时间之间的关系为 ,该函数图象过 , 两点,代入得
解得
当 时A方案的移动通讯费用与时间之间的关系为 ,
由图象可知,当 时 ,
A方案费用与时间的关系为 ,
同理可得B方案费用与时间的关系为 ,
由图象可知,若通话时间少于 分钟,则A方案比B方案便宜 元,故A正确;
由图象可知,当 时,A方案与B方案通话时间一样多.
若 ,B方案比A方案的通话时间多,故B正确;
若两种方案通讯费用相差 元,则 或 ,
解得 或 ,故C错误;
由图象可知,若通话时间超过 分,则B方案比A方案便宜 元,故D正确.
10. C
第二部分
11. ,
12. ,,
13. 或
【解析】由直角三角形的三边长为 ,,,分两种情况考虑:
(i)当 为斜边时,根据勾股定理得:,即 ,解得:,
直角三角形的三边分别为 ,,,即 为最短边,则最短边上的高为 ;
(ii)当 为斜边时, 为最短边,此时 边上的高为 .
综上,最短边上的高为 或 .
14.
【解析】把 , 代入 ,可得:
解得:
不等式为 ,
解得,.
15.
16. 或
第三部分
17. (1) 过点 且与已知直线 平行,
设过 点的直线为 .
把 代入 ,
.
;
画图如下:
??????(2)
【解析】因为 ,则直线 为 ,
由此可得点 的坐标为 ,
当点 在 点的左侧时,,
当点 在 点的右侧时,,
18. (1)
??????(2) ;
19. (1) 设乙车所行使路程 与时间 的函数关系式为 .
把 和 代入,得
解得:
故 与 的函数关系式为 .
??????(2) 设线段 对应的函数关系式为 ,
把 , 代入,得
解得
故 与 的函数关系式为 ,
则当 时,.
可得:点 的纵坐标为 ,
表示因故停车检修,
交点 的纵坐标为 ,
把 代入 中,有 ,
解得 ,
则交点 的坐标为 ,
交点 表示第一次相遇,
乙车出发 小时,两车在途中第一次相遇.
20. (1) 因为点 的横坐标为 ,且在直线 上,
所以点 的坐标为 ,
因为直线 是由直线 向下平移 个单位长度而得,
所以直线 的解析式为 .
因为点 在直线 上,且纵坐标为 ,
所以点 的坐标为 .
设直线 的解析式为 ,
将点 , 代入 得:
解得
所以直线 的解析式为 .
??????(2) 过点 作 轴的垂线,垂足为点 .
因为点 的坐标为 ,
所以 .
因为点 是直线 与 轴的交点,
所以点 的坐标为 .
因为点 是直线 与 轴的交点,
所以点 的坐标为 .
所以 .
所以 的面积 .
21. (1) 设甲仓库存放原料 吨,乙仓库存放原料 吨.
根据题意得:
解得
故甲仓库存放原料 吨,乙仓库存放原料 吨.
??????(2) 据题意,从甲仓库运 吨原料到工厂,则从乙仓库运 吨原料到工厂,
则 .
??????(3) ①当 时,,由一次函数的性质可知, 随着 的增大而增大;
②当 时,, 随着 的增大没有变化;
③当 时,则 , 随着 的增大而减小.
22. (1)
??????(2) 当每套楼房赠送的装修费多于 元时,方案一合算;当每套楼房赠送的装修费等于 元时方案一同方案二一样合算;当每套楼房赠送的装修费少于 元时,方案二合算.
第1页(共1 页)
总分:100分
班级:__________ 姓名:__________ 学号:__________ 得分:__________
一、选择题(共10小题;共30分)
1. 平面直角坐标系内 轴,,点 的坐标为 ,则点 的坐标为
A. B.
C. 或 D. 或
2. 小敏从 A 地出发向 B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点 的两条线段 , 分别表示小敏、小聪离B地的距离 与已用时间 之间的关系,则小敏、小聪行走的速度分别是
A. 和 B. 和
C. 和 D. 和
3. 实数 在数轴上对应的点如图所示,则 的大小关系正确的是 .
A. B. C. D.
4. 若等腰三角形中的一个外角等于 ,则它的顶角的度数是
A. B. C. D. 或
5. 一段笔直的公路 长 千米,途中有一处休息点 , 长 千米.甲、乙两名长跑爱好者同时从点 出发.甲以 千米/时的速度匀速跑至点 ,原地休息半小时后,再以 千米/时的速度匀速跑至终点 ;乙以 千米/时的速度匀速跑至终点 .下列选项中,能正确反映甲、乙两人出发后 小时内运动路程 (千米)与时间 (小时)函数关系的图象是
A. B.
C. D.
6. 函数 与 的图象如图所示,则不等式 的解集是
A. B. C. D.
7. 一个等腰三角形一边长为 ,另一边长为 ,那么这个等腰三角形的周长是
A. B. C. 或 D. 以上都不对
8. 不等式组 的解集为 ,则 满足的条件是
A. B. C. D.
9. 如图,某电脑公司提供了A,B两种方案的移动通讯费用 (元)与通话时间 (分钟)之间的关系,则以下说法错误的是
A. 若通话时间少于 分,则A方案比B方案便宜 元
B. 若通讯费用为 元,则B方案比A方案的通话时间多
C. 若两种方案通讯费用相差 元,则通话时间是 分或 分
D. 若通话时间超过 分,则B方案比A方案便宜 元
10. 一辆小汽车从甲地驶往乙地,一辆客车从乙地驶往甲地,两车同时出发.设客车行驶的时间为 ,两车之间的距离为 ,图中折线表示 与 之间的函数关系.则下列说法:① 甲乙两地之间的距离为 ;② 点 表示两车相遇;③ 客车速度为 ;④ 线段 所表示的 与 的函数关系是 ;⑤ 若第二辆小汽车也从甲地驶往乙地,速度与第一辆小汽车相同.在第一辆小汽车与客车相遇 分钟后,第二辆小汽车与客车相遇,则第二辆小汽车比第一辆小汽车晚出发 .其中正确的有
A. 个 B. 个 C. 个 D. 个
二、填空题(共6小题;共18分)
11. 已知等腰三角形的周长为 ,设它的腰长为 ,底边长为 ,则 与 的函数关系式是 ?;其中自变量是 ?.
12. 张老师带领 名学生到某动物园参观,已知成人票每张 元,学生票每张 元,设门票的总费用为 元,则 ?;其中自变量是 ?,自变量的函数是 ?.
13. 如果直角三角形的三边长为 ,,,则最短边上的高为 ?.
14. 如图,一次函数 的图象经过 , 两点,则 解集是 ?.
15. 如图,已知一次函数 与一次函数 的图象相交于点 ,则不等式 的解集是 ?.
16. 已知线段 平行于 轴,且 的长度为 ,若 ,则点 的坐标 ?.
三、解答题(共6小题;共52分)
17. (1)求过点 且与已知直线 平行的直线 的函数表达式,并画出直线 的图象;
(2)设直线 分别与 轴、 轴交于点 、点 ,如果直线 与直线 平行且交 轴于点 ,求出 的面积 关于 的函数表达式.
18. 已知一次函数的图象与正比例函数 的图象平行,且经过点 .
(1)求一次函数的解析式.
(2)若点 和 在一次函数的图象上,求 , 的值.
19. 甲、乙两辆汽车沿同一路线赶赴距出发地 千米的目的地,乙车比甲车晚出发 小时(从甲车出发时开始计时),图中折线 ,线段 分别表示甲、乙两车所行路程 (千米)与时间 (小时)之间的函数关系对应的图象(线段 表示甲出发不足 小时因故停车检修),请根据图象所提供的信息,解决如下问题:
(1)求乙车所行路程 与时间 的函数关系式;
(2)乙车出发多长时间,两车在途中第一次相遇?(要写出解题过程)
20. 如图,在平面直角坐标系中,直线 与直线 交点 的横坐标为 ,将直线 沿 轴向下平移 个单位长度,得到直线 ,直线 与 轴交于点 ,与直线 交于点 ,点 的纵坐标为 ,直线 与 轴交于点 .
(1)求直线 的解析式;
(2)求 的面积.
21. 某公司在甲、乙仓库共存放某种原料 吨,如果运出甲仓库所存原料的 ,乙仓库所存原料的 ,那么乙仓库剩余的原料比甲仓库剩余的原料多 吨.
(1)求甲、乙两仓库各存放原料多少吨?
(2)现公司需将 吨原料运往工厂,从甲、乙两个仓库到工厂的运价分别为 元/吨和 元/吨.经协商,从甲仓库到工厂的运价可优惠 元/吨 ,从乙仓库到工厂的运价不变,设从甲仓库运 吨原料到工厂,请求出总运费 关于 的函数解析式(不要求写出 的取值范围);
(3)在()的条件下,请根据函数的性质说明:随着 的增大, 的变化情况.
22. 新农村社区改造中,有一部分楼盘要对外销售.某楼盘共 层,销售价格如下:第八层楼房售价为 元/平方米,从第八层起每上升一层,每平方米的售价提高 元;反之,楼层每下降一层,每平方米的售价降低 元,已知该楼盘每套楼房面积均为 平方米.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价 ,另外每套楼房赠送 元装修基金;
方案二:降价 ,没有其他赠送.
(1)请写出售价 (元/平方米)与楼层 之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
答案
第一部分
1. C
2. D
3. D
4. D
5. A
【解析】本题考查一次函数图象的实际应用.甲匀速跑至 点用时 小时 ,原地休息半小时此时 ,再以 千米/时的速度匀速跑至终点 ,
千米, 千米,
千米,
甲从 至 还需 小时,
甲跑 段 ;乙跑 千米/时的速度匀速跑到点 ,则 ,当 时,.
6. B
7. C 【解析】当 为等腰三角形的腰时,
三角形的三边分别是 ,, 符合三角形的三边关系,
周长为 ;
当 为等腰三角形的腰时,
三边分别是 ,,,符合三角形的三边关系,
周长为 .
8. D 【解析】解不等式组得:
不等式组 的解 ,
.
9. C 【解析】设 时A方案的移动通讯费用与时间之间的关系为 ,该函数图象过 , 两点,代入得
解得
当 时A方案的移动通讯费用与时间之间的关系为 ,
由图象可知,当 时 ,
A方案费用与时间的关系为 ,
同理可得B方案费用与时间的关系为 ,
由图象可知,若通话时间少于 分钟,则A方案比B方案便宜 元,故A正确;
由图象可知,当 时,A方案与B方案通话时间一样多.
若 ,B方案比A方案的通话时间多,故B正确;
若两种方案通讯费用相差 元,则 或 ,
解得 或 ,故C错误;
由图象可知,若通话时间超过 分,则B方案比A方案便宜 元,故D正确.
10. C
第二部分
11. ,
12. ,,
13. 或
【解析】由直角三角形的三边长为 ,,,分两种情况考虑:
(i)当 为斜边时,根据勾股定理得:,即 ,解得:,
直角三角形的三边分别为 ,,,即 为最短边,则最短边上的高为 ;
(ii)当 为斜边时, 为最短边,此时 边上的高为 .
综上,最短边上的高为 或 .
14.
【解析】把 , 代入 ,可得:
解得:
不等式为 ,
解得,.
15.
16. 或
第三部分
17. (1) 过点 且与已知直线 平行,
设过 点的直线为 .
把 代入 ,
.
;
画图如下:
??????(2)
【解析】因为 ,则直线 为 ,
由此可得点 的坐标为 ,
当点 在 点的左侧时,,
当点 在 点的右侧时,,
18. (1)
??????(2) ;
19. (1) 设乙车所行使路程 与时间 的函数关系式为 .
把 和 代入,得
解得:
故 与 的函数关系式为 .
??????(2) 设线段 对应的函数关系式为 ,
把 , 代入,得
解得
故 与 的函数关系式为 ,
则当 时,.
可得:点 的纵坐标为 ,
表示因故停车检修,
交点 的纵坐标为 ,
把 代入 中,有 ,
解得 ,
则交点 的坐标为 ,
交点 表示第一次相遇,
乙车出发 小时,两车在途中第一次相遇.
20. (1) 因为点 的横坐标为 ,且在直线 上,
所以点 的坐标为 ,
因为直线 是由直线 向下平移 个单位长度而得,
所以直线 的解析式为 .
因为点 在直线 上,且纵坐标为 ,
所以点 的坐标为 .
设直线 的解析式为 ,
将点 , 代入 得:
解得
所以直线 的解析式为 .
??????(2) 过点 作 轴的垂线,垂足为点 .
因为点 的坐标为 ,
所以 .
因为点 是直线 与 轴的交点,
所以点 的坐标为 .
因为点 是直线 与 轴的交点,
所以点 的坐标为 .
所以 .
所以 的面积 .
21. (1) 设甲仓库存放原料 吨,乙仓库存放原料 吨.
根据题意得:
解得
故甲仓库存放原料 吨,乙仓库存放原料 吨.
??????(2) 据题意,从甲仓库运 吨原料到工厂,则从乙仓库运 吨原料到工厂,
则 .
??????(3) ①当 时,,由一次函数的性质可知, 随着 的增大而增大;
②当 时,, 随着 的增大没有变化;
③当 时,则 , 随着 的增大而减小.
22. (1)
??????(2) 当每套楼房赠送的装修费多于 元时,方案一合算;当每套楼房赠送的装修费等于 元时方案一同方案二一样合算;当每套楼房赠送的装修费少于 元时,方案二合算.
第1页(共1 页)
