人教版数学八年级下册 第二十章 数据的分析 单元检测卷(含答案)
文档属性
| 名称 | 人教版数学八年级下册 第二十章 数据的分析 单元检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 10:19:13 | ||
图片预览


文档简介
第二十章 数据的分析 单元检测卷
总分:100分
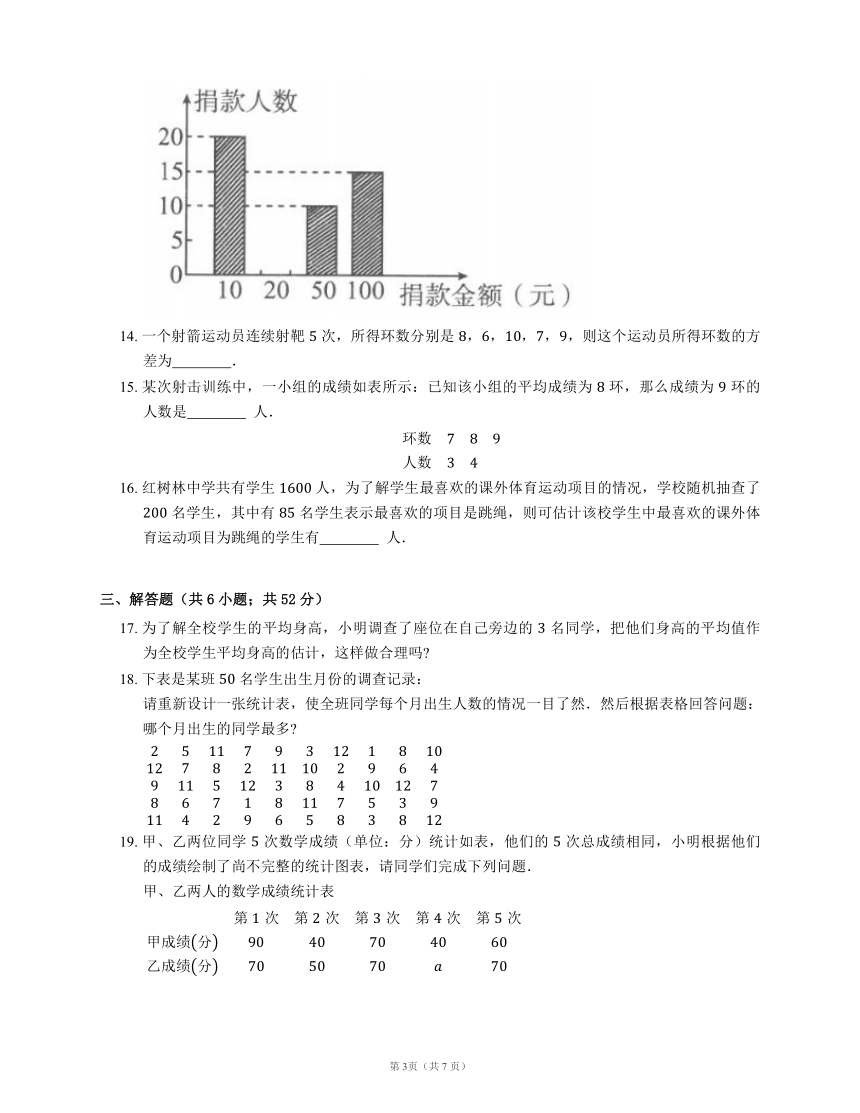
班级:__________ 姓名:__________ 学号:__________ 得分:__________
一、选择题(共10小题;共30分)
1. 在 ,,,,, 中正确的是
A. 平均数 B. 众数是 C. 中位数是 D. 极差为
2. 为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,并设置了“赞成、反对、无所谓”三种意见.现从学校所有 名学生中随机征求了 名学生的意见,其中持“反对”和“无所谓”意见的共有 名学生,估计全校持“赞成”意见的学生人数约为
A. B. C. D.
3. 在频数分布表中,各小组的频数之和
A. 小于数据总数 B. 等于数据总数 C. 大于数据总数 D. 不能确定
4. 下列数据:,,,,,则这组数据的众数和极差是
A. , B. , C. , D. ,
5. 某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是
A. 第一天 B. 第二天 C. 第三天 D. 第四天
6. 小明参加 短跑训练, 年 月的训练成绩如表所示:
体育老师夸奖小明是“田径天才”.请你预测小明 年( 个月)后 短跑的成绩为
(温馨提示:目前 短跑世界记录为 秒 )
A. B.
C. D. 预测结果不可靠
7. 某同学参加数学、物理、化学三科竞赛平均成绩是 分,其中数学 分,化学 分,那么物理成绩是
A. 分 B. 分 C. 分 D. 分
8. 已知甲、乙、丙、丁共有课外书 本,又知甲、乙、丙、丁的课外书制作的条形统计图的高度之比为 ,则乙的课外书的本数为
A. 本 B. 本 C. 本 D. 本
9. 在一次“爱心义卖活动”中,某校 年级的六个班级捐献的义卖金额数据如下: 元, 元, 元, 元, 元, 元.这组数据的众数和中位数分别是
A. 元, 元 B. 元, 元
C. 元, 元 D. 元, 元
10. 某校对全体学生开展心理健康知识测试,七、八、九三个年级共有 名学生,各年级的合格人数如表所示,则下列说法正确的是
A. 七年级的合格率最高
B. 八年级的学生人数为 名
C. 八年级的合格率高于全校的合格率
D. 九年级的合格人数最少
二、填空题(共6小题;共18分)
11. 已知数据 ,,,,,,,,,,则这组数据的众数为 ?.
12. 如图,是某市 月 日至 月 日每天最高、最低气温的折线统计图,在这 天中,日温差最大的一天是 ? 日.
13. 在某公益活动中,小明对本年级同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐 元的人数占本年级捐款总人数的 ,则本次捐款 元的人数为 ? 人.
14. 一个射箭运动员连续射靶 次,所得环数分别是 ,,,,,则这个运动员所得环数的方差为 ?.
15. 某次射击训练中,一小组的成绩如表所示:已知该小组的平均成绩为 环,那么成绩为 环的人数是 ? 人.
16. 红树林中学共有学生 人,为了解学生最喜欢的课外体育运动项目的情况,学校随机抽查了 名学生,其中有 名学生表示最喜欢的项目是跳绳,则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有 ? 人.
三、解答题(共6小题;共52分)
17. 为了解全校学生的平均身高,小明调查了座位在自己旁边的 名同学,把他们身高的平均值作为全校学生平均身高的估计,这样做合理吗?
18. 下表是某班 名学生出生月份的调查记录:
请重新设计一张统计表,使全班同学每个月出生人数的情况一目了然.然后根据表格回答问题:哪个月出生的同学最多?
19. 甲、乙两位同学 次数学成绩(单位:分)统计如表,他们的 次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
甲、乙两人的数学成绩统计表
(1) ?, ?;
(2)请完成图中表示乙成绩变化情况的折线;
(3),乙成绩的方差是 ?,可看出 ? 的成绩比较稳定(填“甲”或“乙”).从平均数和方差的角度分析, ? 将被选中(填“甲”或“乙”).
20. 某校要从小王和小李两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表(单位:分):
根据上表解答下列问题.
(1)完成下表:
(2)在这五次测试中,成绩比较稳定的同学是谁?若将 分以上(含 分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到 分以上(含 分)就很可能获奖,成绩达到 分以上(含 分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由
21. 张明、李成两位同学初二学年 次数学单元自我检测的成绩(成绩均为整数,且个位数为 )分别如下图所示:利用图中提供的信息,解答下列问题.
(1)完成下表:
(2)如果将 分以上(含 分)的成绩视为优秀,则优秀率高的同学是 ?;
(3)根据图表信息,请你对这两位同学各提一条不超过 个字的学习建议.
22. 某校八年级(1)班 名学生参加 年贵阳市数学质量监控考试,全班学生的成绩统计如下表:
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数是 ?.
(2)该班学生考试成绩的中位数是 ?.
(3)该班张华同学在这次考试中的成绩是 分,能不能说张华同学的成绩处于全班中游偏上水平?试说明理由.
答案
第一部分
1. D
2. C
3. B
4. A
5. B
【解析】由图象中的信息可知,,利润最大的天数是第二天.
6. D
7. C
8. A
9. D 【解析】 出现了 次,次数最多,故众数为 ;把这组数据按照从小到大的顺序排列为, 元, 元, 元, 元, 元, 元,故中位数为 .
10. D
第二部分
11.
12.
13.
14.
15.
16.
第三部分
17. 不合理.
18. 统计表如下:
8月份出生的同学最多.
19. (1) ;
??????(2) 如图所示:
??????(3) ;乙;乙
20. (1) ;;;
??????(2) 成绩比较稳定的是小李;小王优秀率为 ,小李优秀率为
??????(3) 若想获奖,选小李;若想得一等奖,选小王.
21. (1)
??????(2) 李成
【解析】如果将 分以上(含 分)的成绩视为优秀,则优秀率高的同学是李成.
??????(3) 李成的学习要持之以恒,保持稳定;张明的学习还需加把劲,提高优秀率.
22. (1)
??????(2)
??????(3) 不能说张华的成绩处于中游偏上的水平,因为全班成绩的中位数是 , 分低于全班成绩的中位数.
第1页(共1 页)
总分:100分
班级:__________ 姓名:__________ 学号:__________ 得分:__________
一、选择题(共10小题;共30分)
1. 在 ,,,,, 中正确的是
A. 平均数 B. 众数是 C. 中位数是 D. 极差为
2. 为了鼓励学生课外阅读,学校公布了“阅读奖励”方案,并设置了“赞成、反对、无所谓”三种意见.现从学校所有 名学生中随机征求了 名学生的意见,其中持“反对”和“无所谓”意见的共有 名学生,估计全校持“赞成”意见的学生人数约为
A. B. C. D.
3. 在频数分布表中,各小组的频数之和
A. 小于数据总数 B. 等于数据总数 C. 大于数据总数 D. 不能确定
4. 下列数据:,,,,,则这组数据的众数和极差是
A. , B. , C. , D. ,
5. 某商品四天内每天每斤的进价与售价信息如图所示,则售出这种商品每斤利润最大的是
A. 第一天 B. 第二天 C. 第三天 D. 第四天
6. 小明参加 短跑训练, 年 月的训练成绩如表所示:
体育老师夸奖小明是“田径天才”.请你预测小明 年( 个月)后 短跑的成绩为
(温馨提示:目前 短跑世界记录为 秒 )
A. B.
C. D. 预测结果不可靠
7. 某同学参加数学、物理、化学三科竞赛平均成绩是 分,其中数学 分,化学 分,那么物理成绩是
A. 分 B. 分 C. 分 D. 分
8. 已知甲、乙、丙、丁共有课外书 本,又知甲、乙、丙、丁的课外书制作的条形统计图的高度之比为 ,则乙的课外书的本数为
A. 本 B. 本 C. 本 D. 本
9. 在一次“爱心义卖活动”中,某校 年级的六个班级捐献的义卖金额数据如下: 元, 元, 元, 元, 元, 元.这组数据的众数和中位数分别是
A. 元, 元 B. 元, 元
C. 元, 元 D. 元, 元
10. 某校对全体学生开展心理健康知识测试,七、八、九三个年级共有 名学生,各年级的合格人数如表所示,则下列说法正确的是
A. 七年级的合格率最高
B. 八年级的学生人数为 名
C. 八年级的合格率高于全校的合格率
D. 九年级的合格人数最少
二、填空题(共6小题;共18分)
11. 已知数据 ,,,,,,,,,,则这组数据的众数为 ?.
12. 如图,是某市 月 日至 月 日每天最高、最低气温的折线统计图,在这 天中,日温差最大的一天是 ? 日.
13. 在某公益活动中,小明对本年级同学的捐款情况进行了统计,绘制成如图所示的不完整的统计图,其中捐 元的人数占本年级捐款总人数的 ,则本次捐款 元的人数为 ? 人.
14. 一个射箭运动员连续射靶 次,所得环数分别是 ,,,,,则这个运动员所得环数的方差为 ?.
15. 某次射击训练中,一小组的成绩如表所示:已知该小组的平均成绩为 环,那么成绩为 环的人数是 ? 人.
16. 红树林中学共有学生 人,为了解学生最喜欢的课外体育运动项目的情况,学校随机抽查了 名学生,其中有 名学生表示最喜欢的项目是跳绳,则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有 ? 人.
三、解答题(共6小题;共52分)
17. 为了解全校学生的平均身高,小明调查了座位在自己旁边的 名同学,把他们身高的平均值作为全校学生平均身高的估计,这样做合理吗?
18. 下表是某班 名学生出生月份的调查记录:
请重新设计一张统计表,使全班同学每个月出生人数的情况一目了然.然后根据表格回答问题:哪个月出生的同学最多?
19. 甲、乙两位同学 次数学成绩(单位:分)统计如表,他们的 次总成绩相同,小明根据他们的成绩绘制了尚不完整的统计图表,请同学们完成下列问题.
甲、乙两人的数学成绩统计表
(1) ?, ?;
(2)请完成图中表示乙成绩变化情况的折线;
(3),乙成绩的方差是 ?,可看出 ? 的成绩比较稳定(填“甲”或“乙”).从平均数和方差的角度分析, ? 将被选中(填“甲”或“乙”).
20. 某校要从小王和小李两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表(单位:分):
根据上表解答下列问题.
(1)完成下表:
(2)在这五次测试中,成绩比较稳定的同学是谁?若将 分以上(含 分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到 分以上(含 分)就很可能获奖,成绩达到 分以上(含 分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由
21. 张明、李成两位同学初二学年 次数学单元自我检测的成绩(成绩均为整数,且个位数为 )分别如下图所示:利用图中提供的信息,解答下列问题.
(1)完成下表:
(2)如果将 分以上(含 分)的成绩视为优秀,则优秀率高的同学是 ?;
(3)根据图表信息,请你对这两位同学各提一条不超过 个字的学习建议.
22. 某校八年级(1)班 名学生参加 年贵阳市数学质量监控考试,全班学生的成绩统计如下表:
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数是 ?.
(2)该班学生考试成绩的中位数是 ?.
(3)该班张华同学在这次考试中的成绩是 分,能不能说张华同学的成绩处于全班中游偏上水平?试说明理由.
答案
第一部分
1. D
2. C
3. B
4. A
5. B
【解析】由图象中的信息可知,,利润最大的天数是第二天.
6. D
7. C
8. A
9. D 【解析】 出现了 次,次数最多,故众数为 ;把这组数据按照从小到大的顺序排列为, 元, 元, 元, 元, 元, 元,故中位数为 .
10. D
第二部分
11.
12.
13.
14.
15.
16.
第三部分
17. 不合理.
18. 统计表如下:
8月份出生的同学最多.
19. (1) ;
??????(2) 如图所示:
??????(3) ;乙;乙
20. (1) ;;;
??????(2) 成绩比较稳定的是小李;小王优秀率为 ,小李优秀率为
??????(3) 若想获奖,选小李;若想得一等奖,选小王.
21. (1)
??????(2) 李成
【解析】如果将 分以上(含 分)的成绩视为优秀,则优秀率高的同学是李成.
??????(3) 李成的学习要持之以恒,保持稳定;张明的学习还需加把劲,提高优秀率.
22. (1)
??????(2)
??????(3) 不能说张华的成绩处于中游偏上的水平,因为全班成绩的中位数是 , 分低于全班成绩的中位数.
第1页(共1 页)
