湘教版九年级数学下册 1.5 二次函数的应用 同步测试含答案
文档属性
| 名称 | 湘教版九年级数学下册 1.5 二次函数的应用 同步测试含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 238.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 06:54:38 | ||
图片预览

文档简介
1.5 二次函数的应用
同步测试
选择题
1. 如图,从地面竖立向上抛出一个小球,小球的高度(单位:)与 小球运动时间t(单位:s)之间的关系式为,那么小球从抛出至回落到地面所需要的时间是:( )
A.6s B.4s C.3s D.2s
2.芳芳在平面直角坐标系画了一个二次函数的图象,并将该图象的特点写在如图所示的卡 片上,则该二次函数的解析式为( )
①开口向下;②顶点是原点;③过点(6,﹣6).
A.y=﹣ B.y= C.y=﹣6x2 D.y=6x2
3.某种电缆在空中架设时,两端挂起的电缆下垂都近似抛物线y=x2的形状.今在一个坡度为1:5的斜坡上,沿水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱(如图),这种情况下在竖直方向上,下垂的电缆与地面的最近距离为( )
A.?12.75米????B.?13.75米??C.?14.75米???D.?17.75米
4.如图,二次函数 y=x2+bx+c 的图象过点 B(0,﹣2).它与反比例函数 y=﹣的图象交 于点 A(m,4),则这个二次函数的解析式为( )
A.y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+2
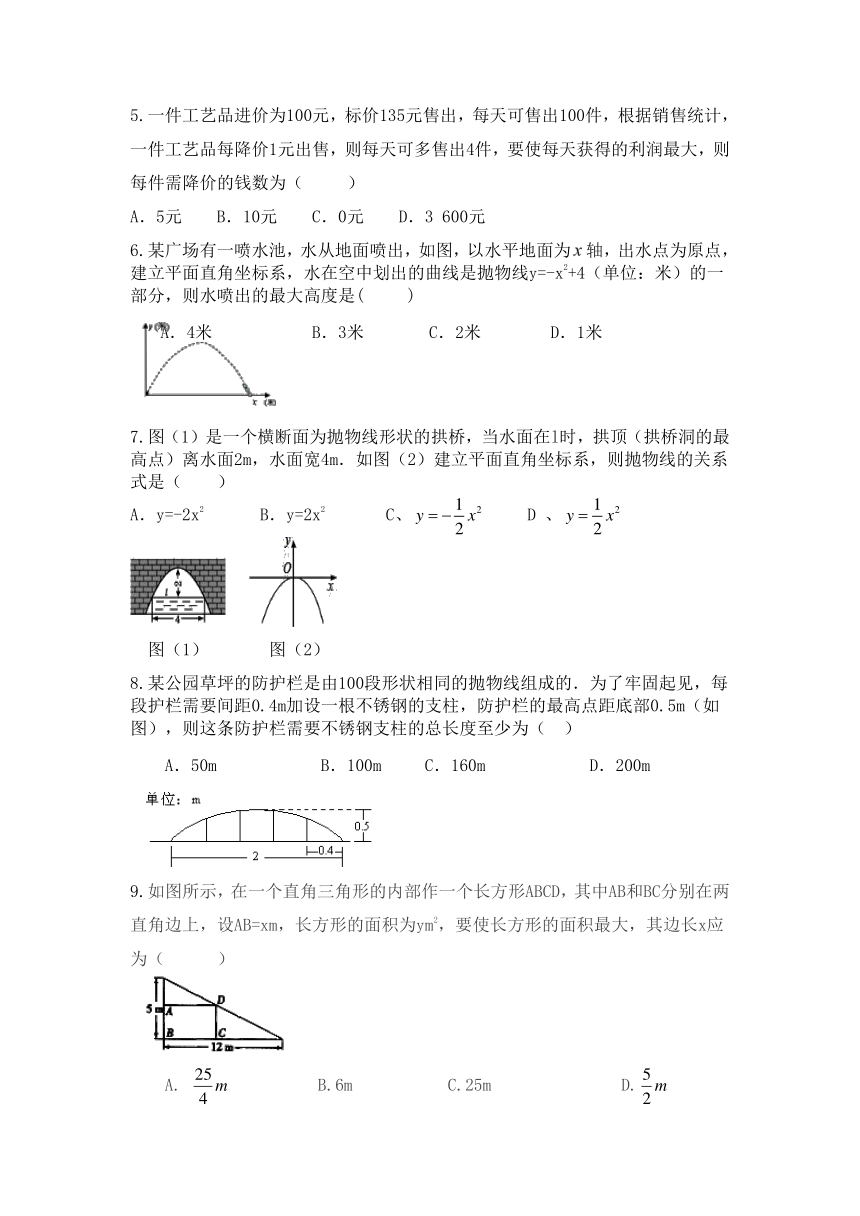
5.一件工艺品进价为100元,标价135元售出,每天可售出100件,根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,则每件需降价的钱数为( )
A.5元 ? B.10元 ? C.0元 ? D.3 600元
6.某广场有一喷水池,水从地面喷出,如图,以水平地面为轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米
7.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A.y=-2x2 B.y=2x2 C、 D 、
图(1) 图(2)
8.某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
9.如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
A. B.6m C.25m D.
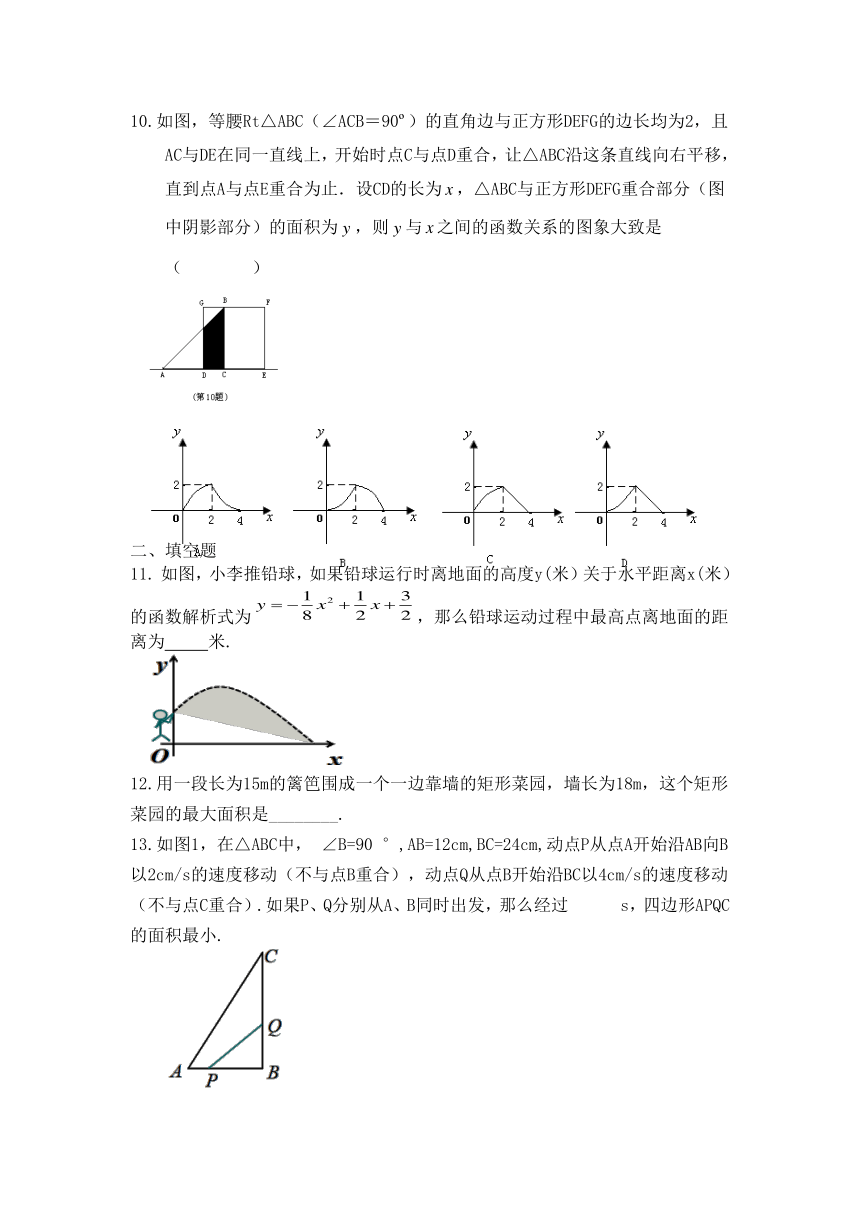
10.如图,等腰Rt△ABC(∠ACB=90?)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为,则与之间的函数关系的图象大致是( )
填空题
如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为,那么铅球运动过程中最高点离地面的距离为 米.
12.用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形菜园的最大面积是________.
13.如图1,在△ABC中, ∠B=90 °,AB=12cm,BC=24cm,动点P从点A开始沿AB向B以2cm/s的速度移动(不与点B重合),动点Q从点B开始沿BC以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过 s,四边形APQC的面积最小.
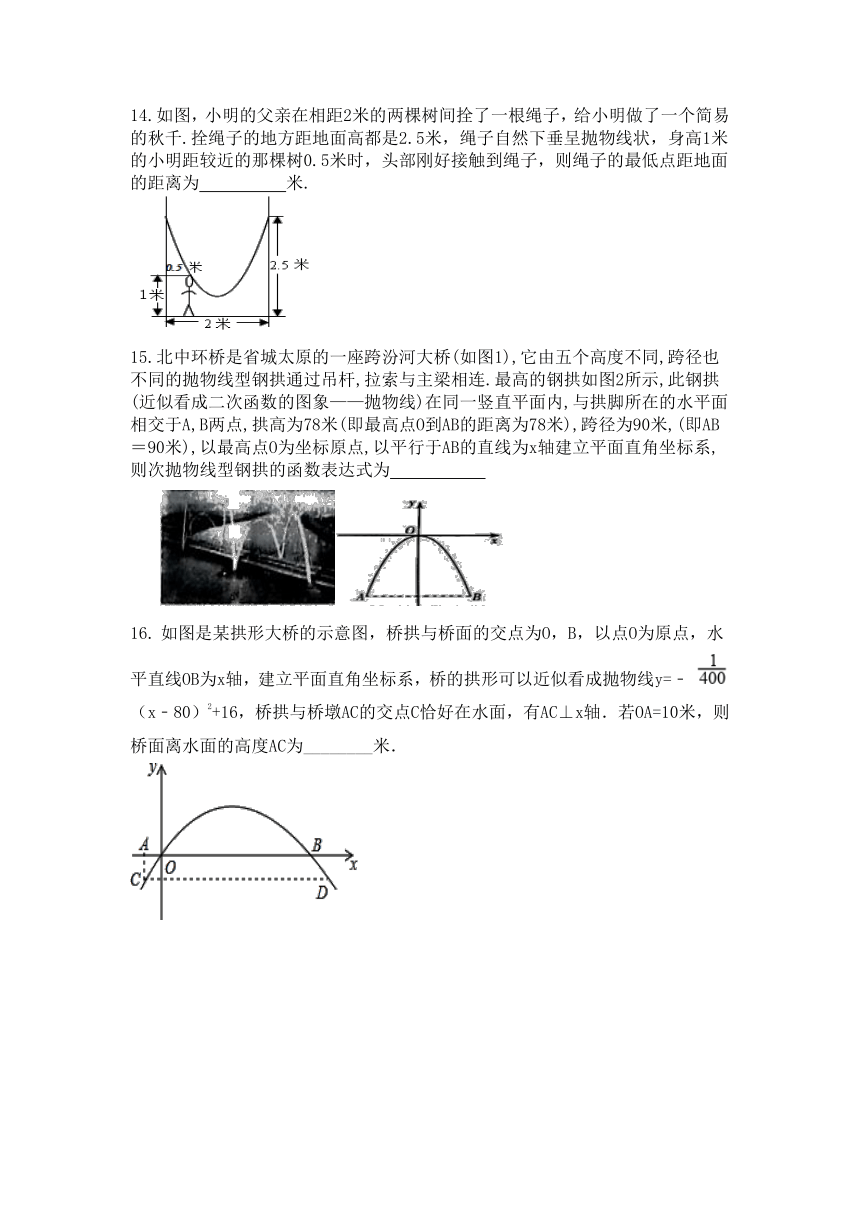
14.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
15.北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连.最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米,(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则次抛物线型钢拱的函数表达式为
如图是某拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=﹣ (x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10米,则桥面离水面的高度AC为________米.
综合题
17.某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
18.一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.
需求量x/kg 50 40 30 20
蔬菜售价Q/(元/kg) 10 15 20 25
19.某蔬菜专业户试种植了一种紧销蔬菜(都能卖出),其中每千克的成本P在9元/kg的基础上,还有一些上浮.若浮动价(元/kg)与需求量x(kg)成反比,比例系数为30.市场连续四天调查发现,蔬菜售价Q(元/kg)与市场需求量x(kg)有如下关系:
(1)直接写出每千克的成本P与需求量x的关系式:________________;
(2)求Q与x的关系式;
(3)当某天的利润率达到100%时,求这天的需求量;
(4)求需求量是多少千克时,利润达到最大值,最大值是多少?
20.某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/kg,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量y(kg)与销售单价x(元/kg)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4 800 kg,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
1.5 二次函数的应用
同步测试答案
选择题
1.A 2.A 3.B 4.A 5.A 6.A 7.D 8.C 9.D 10.A
二、填空题
11. 2
12.
13.3
14.
15.y=x2
16.
三、综合题
17.解:(1)根据题意,得,
即.
(2)由题意,得.
整理,得.
解这个方程,得.
要使百姓得到实惠,取.所以,每台冰箱应降价200元.
(3)对于,
当时,
.
所以,每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元.
18.解析:(1)根据题目条件,的坐标分别是.
设抛物线的解析式为,
将的坐标代入,得
解得.
所以抛物线的表达式是.
(2)可设,于是
从而支柱的长度是米.
(3)设是隔离带的宽,是三辆车的宽度和,
则点坐标是.
过点作垂直交抛物线于,则.
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.
19.解:(1)P=9+;
(2)由观察发现需求量每减少10 kg,蔬菜售价会增加5元/kg,则Q与x是一次函数关系.
设Q与x的关系式为Q=kx+b.
把(50,10),(40,15)代入上式,得
,解得
∴Q与x的关系式为Q=-x+35;
(3)∵利润率为100%,
∴Q-P=P,即-x+35-9-=9+.
整理,得x2-34x+120=0.
解得x1=30,x2=4.
经检验,x1=30,x2=4是原方程的解.
答:这天的需求量为30 kg或4 kg;
(4)由(3)知,
W1=-x2+26x-30=-(x-26)2+308.
∵-<0,∴函数有最大值.
∴当x=26,即需求量是26 kg时,利润达到最大值,最大利润是308元.
20.解:(1)设y与x的函数关系式为y=kx+b(k≠0).把(10,200),(15,150)代入y=kx+b,得
解得
∴y与x的函数关系式为y=-10x+300.
由-10x+300≥0,得x≤30.
∴x的取值范围为8≤x≤30;
(2)设该品种蜜柚定价为x元/kg时,每天销售利润为W元.根据题意,得
W=(x-8)(-10x+300)
=-10(x-19)2+1 210.
∵a=-10<0,
∴当x=19时,W最大值=1 210.
答:当该品种蜜柚定价为19元/kg时,每天销售获得的利润最大,最大利润是1 210元;
(3)不能.
理由:根据(2)中获得最大利润的方式进行销售时,定价为19元/kg,则
y=-10×19+300=110.
∴110×40=4 400<4 800.
∴该农户不能销售完这批蜜柚.
同步测试
选择题
1. 如图,从地面竖立向上抛出一个小球,小球的高度(单位:)与 小球运动时间t(单位:s)之间的关系式为,那么小球从抛出至回落到地面所需要的时间是:( )
A.6s B.4s C.3s D.2s
2.芳芳在平面直角坐标系画了一个二次函数的图象,并将该图象的特点写在如图所示的卡 片上,则该二次函数的解析式为( )
①开口向下;②顶点是原点;③过点(6,﹣6).
A.y=﹣ B.y= C.y=﹣6x2 D.y=6x2
3.某种电缆在空中架设时,两端挂起的电缆下垂都近似抛物线y=x2的形状.今在一个坡度为1:5的斜坡上,沿水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱(如图),这种情况下在竖直方向上,下垂的电缆与地面的最近距离为( )
A.?12.75米????B.?13.75米??C.?14.75米???D.?17.75米
4.如图,二次函数 y=x2+bx+c 的图象过点 B(0,﹣2).它与反比例函数 y=﹣的图象交 于点 A(m,4),则这个二次函数的解析式为( )
A.y=x2﹣x﹣2 B.y=x2﹣x+2 C.y=x2+x﹣2 D.y=x2+x+2
5.一件工艺品进价为100元,标价135元售出,每天可售出100件,根据销售统计,一件工艺品每降价1元出售,则每天可多售出4件,要使每天获得的利润最大,则每件需降价的钱数为( )
A.5元 ? B.10元 ? C.0元 ? D.3 600元
6.某广场有一喷水池,水从地面喷出,如图,以水平地面为轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4(单位:米)的一部分,则水喷出的最大高度是( )
A.4米 B.3米 C.2米 D.1米
7.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A.y=-2x2 B.y=2x2 C、 D 、
图(1) 图(2)
8.某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )
A.50m B.100m C.160m D.200m
9.如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
A. B.6m C.25m D.
10.如图,等腰Rt△ABC(∠ACB=90?)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为,则与之间的函数关系的图象大致是( )
填空题
如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为,那么铅球运动过程中最高点离地面的距离为 米.
12.用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形菜园的最大面积是________.
13.如图1,在△ABC中, ∠B=90 °,AB=12cm,BC=24cm,动点P从点A开始沿AB向B以2cm/s的速度移动(不与点B重合),动点Q从点B开始沿BC以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过 s,四边形APQC的面积最小.
14.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
15.北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连.最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米,(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则次抛物线型钢拱的函数表达式为
如图是某拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=﹣ (x﹣80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10米,则桥面离水面的高度AC为________米.
综合题
17.某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
18.一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.
需求量x/kg 50 40 30 20
蔬菜售价Q/(元/kg) 10 15 20 25
19.某蔬菜专业户试种植了一种紧销蔬菜(都能卖出),其中每千克的成本P在9元/kg的基础上,还有一些上浮.若浮动价(元/kg)与需求量x(kg)成反比,比例系数为30.市场连续四天调查发现,蔬菜售价Q(元/kg)与市场需求量x(kg)有如下关系:
(1)直接写出每千克的成本P与需求量x的关系式:________________;
(2)求Q与x的关系式;
(3)当某天的利润率达到100%时,求这天的需求量;
(4)求需求量是多少千克时,利润达到最大值,最大值是多少?
20.某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节,已知该蜜柚的成本价为8元/kg,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销售量y(kg)与销售单价x(元/kg)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某农户今年共采摘蜜柚4 800 kg,该品种蜜柚的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批蜜柚?请说明理由.
1.5 二次函数的应用
同步测试答案
选择题
1.A 2.A 3.B 4.A 5.A 6.A 7.D 8.C 9.D 10.A
二、填空题
11. 2
12.
13.3
14.
15.y=x2
16.
三、综合题
17.解:(1)根据题意,得,
即.
(2)由题意,得.
整理,得.
解这个方程,得.
要使百姓得到实惠,取.所以,每台冰箱应降价200元.
(3)对于,
当时,
.
所以,每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元.
18.解析:(1)根据题目条件,的坐标分别是.
设抛物线的解析式为,
将的坐标代入,得
解得.
所以抛物线的表达式是.
(2)可设,于是
从而支柱的长度是米.
(3)设是隔离带的宽,是三辆车的宽度和,
则点坐标是.
过点作垂直交抛物线于,则.
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.
19.解:(1)P=9+;
(2)由观察发现需求量每减少10 kg,蔬菜售价会增加5元/kg,则Q与x是一次函数关系.
设Q与x的关系式为Q=kx+b.
把(50,10),(40,15)代入上式,得
,解得
∴Q与x的关系式为Q=-x+35;
(3)∵利润率为100%,
∴Q-P=P,即-x+35-9-=9+.
整理,得x2-34x+120=0.
解得x1=30,x2=4.
经检验,x1=30,x2=4是原方程的解.
答:这天的需求量为30 kg或4 kg;
(4)由(3)知,
W1=-x2+26x-30=-(x-26)2+308.
∵-<0,∴函数有最大值.
∴当x=26,即需求量是26 kg时,利润达到最大值,最大利润是308元.
20.解:(1)设y与x的函数关系式为y=kx+b(k≠0).把(10,200),(15,150)代入y=kx+b,得
解得
∴y与x的函数关系式为y=-10x+300.
由-10x+300≥0,得x≤30.
∴x的取值范围为8≤x≤30;
(2)设该品种蜜柚定价为x元/kg时,每天销售利润为W元.根据题意,得
W=(x-8)(-10x+300)
=-10(x-19)2+1 210.
∵a=-10<0,
∴当x=19时,W最大值=1 210.
答:当该品种蜜柚定价为19元/kg时,每天销售获得的利润最大,最大利润是1 210元;
(3)不能.
理由:根据(2)中获得最大利润的方式进行销售时,定价为19元/kg,则
y=-10×19+300=110.
∴110×40=4 400<4 800.
∴该农户不能销售完这批蜜柚.
