高中数学人教A版选修2-2 利用导数证明不等式 课件(73张ppt)
文档属性
| 名称 | 高中数学人教A版选修2-2 利用导数证明不等式 课件(73张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 00:00:00 | ||
图片预览










文档简介
(共73张PPT)
高二年级 数学
利用导数证明不等式
1
知 识 回 顾
如何利用导数确定函数的最值?
2
知 识 回 顾
如何利用导数确定函数的最值?
明确函数及其定义域
确定极值
判断 的符号
确定 单调性
确定最值
恒正(负)
令
列表
3
求导函数
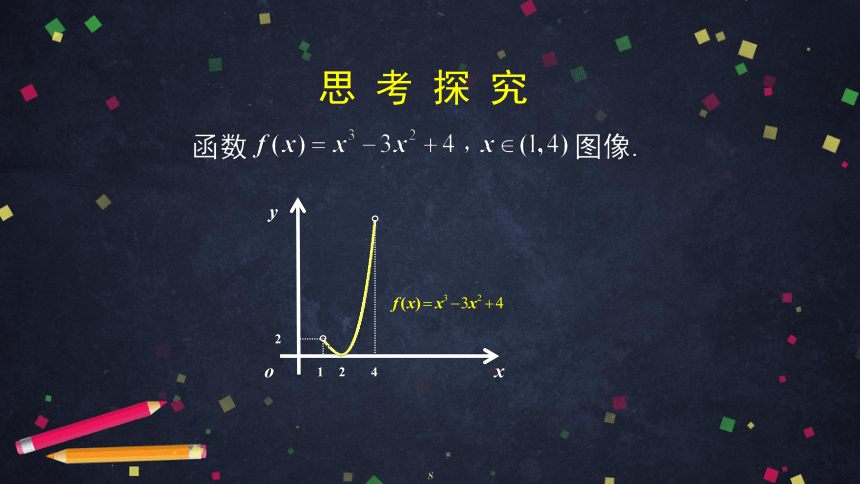
思 考 探 究
4
思 考 探 究
5
思 考 探 究
6
思 考 探 究
7
思 考 探 究
8
思 考 探 究
9
思 考 探 究
10
思 考 探 究
11
思 考 探 究
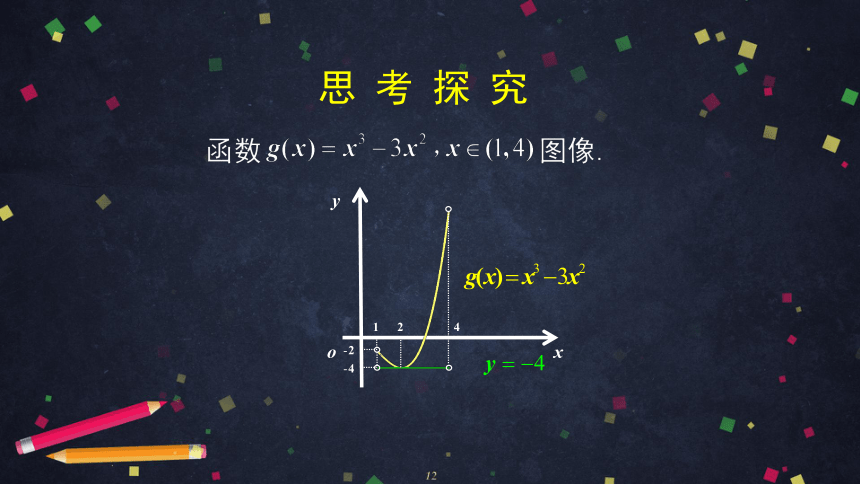
12
比较两种解法
它们的共同点和不同点?
13
两种解法的共同点
14
证明不等式思路
原不
等式
变形
确定最值
证明结论
构建函数
求导函数
确定 单调性
15
不等式一边为常数
通常作差一边化为0
典 型 例 题
16
典 型 例 题
17
变形为
构造函数
求
18
求最小值
19
20
典 型 例 题
21
变形为
构造函数
求
22
23
24
25
26
27
28
左边变形为
29
右边变形为
30
31
32
33
34
35
出现困难
36
37
38
39
40
41
解题思路
构造新函数
变形为
求最值
42
怎样判断
符号?
43
44
45
46
47
48
回 顾 反 思
关键:利用导数证明不等式
变形
设新
函数
确定最值
证明结论
求导函数
判断 的符号
确定 单调性
二次求导
49
50
解题思路
构造新函数
变形为
求最值
51
无法判断
符号
二次求导
52
53
54
【分析】
同学们换一个角度想一想,还有其它的解法吗?
55
解题思路
变形为
构造新函数
求最值
56
所以, .
所以, .
57
回 顾 反 思
变 形
(作差或作商)
确定最值
证明结论
构造函数
判断 的符号
确定 单调性
58
利用导数证明不等式步骤:
作差与0比,
作商与1比.
59
和前面的例题有什么不同?
60
61
62
63
设零点,设而不求
怎样求根?
64
怎样证明大于0?
65
无法证明大于0?
零点存在定理
66
67
设正根为
成立
证明
设零点
求最值
确定 范围
化简
确定范围
求最值
回 顾 反 思
含参不等式的证明
求出最值
不等式 变形
确定 单调性
68
构建新 函数
设零点,确定零点范围
转化与化归,合理替换
课 堂 小 结
1.本节课我们主要解决了什么样的问题?
2.解决此类问题的方法是什么?关键是什么?
3.在解决问题过程中,运用了哪些数学的思想
和方法?
69
课 堂 小 结
70
不等式 证明
导数
函数有关问题
将
不等
式变
形
构建函数
函数最值
判断单调性
方法灵活多样
化为最简
课 堂 小 结
解决“不等式证明”问题的关键:
71
不等式变形
作差或作商
化为最简形式
构建新函数
函数最值问题
课 堂 小 结
在解决问题过程中体会转化与化归,数形结合
等数学思想方法.
72
课 后 作 业
73
高二年级 数学
利用导数证明不等式
1
知 识 回 顾
如何利用导数确定函数的最值?
2
知 识 回 顾
如何利用导数确定函数的最值?
明确函数及其定义域
确定极值
判断 的符号
确定 单调性
确定最值
恒正(负)
令
列表
3
求导函数
思 考 探 究
4
思 考 探 究
5
思 考 探 究
6
思 考 探 究
7
思 考 探 究
8
思 考 探 究
9
思 考 探 究
10
思 考 探 究
11
思 考 探 究
12
比较两种解法
它们的共同点和不同点?
13
两种解法的共同点
14
证明不等式思路
原不
等式
变形
确定最值
证明结论
构建函数
求导函数
确定 单调性
15
不等式一边为常数
通常作差一边化为0
典 型 例 题
16
典 型 例 题
17
变形为
构造函数
求
18
求最小值
19
20
典 型 例 题
21
变形为
构造函数
求
22
23
24
25
26
27
28
左边变形为
29
右边变形为
30
31
32
33
34
35
出现困难
36
37
38
39
40
41
解题思路
构造新函数
变形为
求最值
42
怎样判断
符号?
43
44
45
46
47
48
回 顾 反 思
关键:利用导数证明不等式
变形
设新
函数
确定最值
证明结论
求导函数
判断 的符号
确定 单调性
二次求导
49
50
解题思路
构造新函数
变形为
求最值
51
无法判断
符号
二次求导
52
53
54
【分析】
同学们换一个角度想一想,还有其它的解法吗?
55
解题思路
变形为
构造新函数
求最值
56
所以, .
所以, .
57
回 顾 反 思
变 形
(作差或作商)
确定最值
证明结论
构造函数
判断 的符号
确定 单调性
58
利用导数证明不等式步骤:
作差与0比,
作商与1比.
59
和前面的例题有什么不同?
60
61
62
63
设零点,设而不求
怎样求根?
64
怎样证明大于0?
65
无法证明大于0?
零点存在定理
66
67
设正根为
成立
证明
设零点
求最值
确定 范围
化简
确定范围
求最值
回 顾 反 思
含参不等式的证明
求出最值
不等式 变形
确定 单调性
68
构建新 函数
设零点,确定零点范围
转化与化归,合理替换
课 堂 小 结
1.本节课我们主要解决了什么样的问题?
2.解决此类问题的方法是什么?关键是什么?
3.在解决问题过程中,运用了哪些数学的思想
和方法?
69
课 堂 小 结
70
不等式 证明
导数
函数有关问题
将
不等
式变
形
构建函数
函数最值
判断单调性
方法灵活多样
化为最简
课 堂 小 结
解决“不等式证明”问题的关键:
71
不等式变形
作差或作商
化为最简形式
构建新函数
函数最值问题
课 堂 小 结
在解决问题过程中体会转化与化归,数形结合
等数学思想方法.
72
课 后 作 业
73
