高中数学人教A版选修2-2 利用导数研究函数的零点问题 课件(56张ppt)
文档属性
| 名称 | 高中数学人教A版选修2-2 利用导数研究函数的零点问题 课件(56张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览











文档简介
(共56张PPT)
高二年级 数学
利用导数研究函数的零点问题
复习回顾
问题1 函数零点的定义是什么?
复习回顾
问题2 函数的零点与方程的解的关系是什么?
复习回顾
复习回顾
复习回顾
复习回顾
复习回顾
问题3 函数零点存在定理是什么?
复习回顾
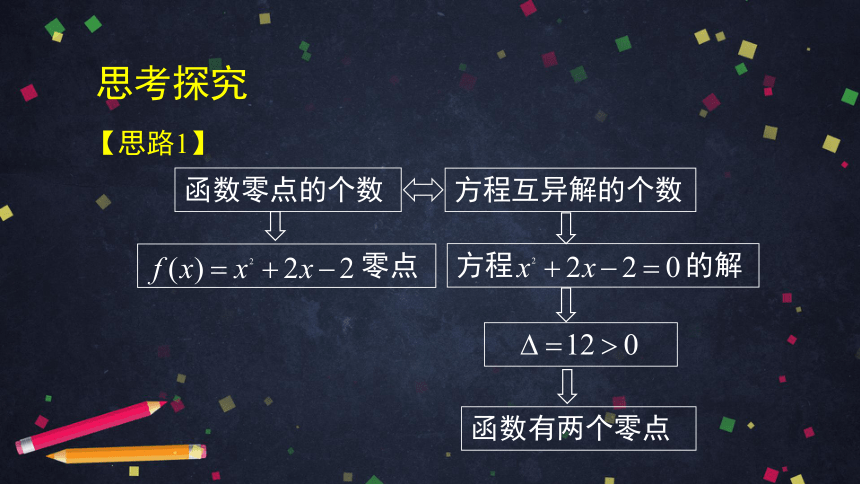
思考探究
思考探究
【思路1】
函数零点的个数
方程互异解的个数
零点
方程 的解
函数有两个零点
思考探究
函数零点的个数
函数图象与 轴交点的个数
研究函数图象
【思路2】
判断函数零点个数的思路
二次函数零点
一元二次方程的解
研究函
数图象
单调性、端点值符号
确定零点
零点存在定理
抛物线的对称轴和开口方向
思考探究
思考探究
判断函数 是否存在零点.
【思路1】
函数零点
函数图象交点
方程的解
方程转化
为函数
函数转化
为方程
思考探究
【思路2】
正确求导
确定导数
符号
确定函数零点个数
确定函数单调性
确定某些点函数值
有且仅有1个零点
判断函数 是否存在零点.
思考探究
没有零点
判断函数 在区间 内是否存在零点.
思考探究
变式:判断函数 在 上零点的个数.
有没有零点?
思考探究
判断函数 在 上零点的个数.
【思路】
,定义域 ,
令 ,可解得 ,
当 x 变化时, 、 的变化情况如下表:
极小值
-1
典例分析
方法1:函数零点转化为方程的解,进而转化为曲线交点.
方法2:研究函数图象与 轴公共点的个数.
【思考】如何判断函数在所给区间内是否存在极值?
函数存在极值
导函数存在
变号的零点
构造新函数
利用导数研究新函数单调性
确定单调区间及单调区间内某些点函数值的符号
研究函数存在极值的解题思路
题后反思
1.正确求导是解决问题的关键.
2.决定导数符号有正负变化的是导数的零点.
3.适时构造新函数.
4.零点存在定理的应用.
回顾反思
1.本节课我们主要研究了什么样的问题?
2.解决此类问题的方法是什么?有什么样的体会?
3.在解决问题过程中,运用了哪些数学思想和方法?
回顾反思
函数的零点问题
函数图象的交点
方程的解
图象与 轴公共点
利用导数研究函数的零点的一般方法和步骤:
明确函数及其定义域
求导函数
判断 的符号
研究 单调性
借助零点存在定理
函数图象
函数零点
研究 极值
研究区间端点值
多角度思考,重视一题多解,体会解法特点,积累解题经验,提高方法识别与选择的能力.
55
回顾反思
函数与方程、函数与不等式、数与形、转化与化归、数形结合、分类与整合……
注重对问题的深入分析和思维训练、分析求解条件、探求求解方向、确定求解思路.
课后作业
高二年级 数学
利用导数研究函数的零点问题
复习回顾
问题1 函数零点的定义是什么?
复习回顾
问题2 函数的零点与方程的解的关系是什么?
复习回顾
复习回顾
复习回顾
复习回顾
复习回顾
问题3 函数零点存在定理是什么?
复习回顾
思考探究
思考探究
【思路1】
函数零点的个数
方程互异解的个数
零点
方程 的解
函数有两个零点
思考探究
函数零点的个数
函数图象与 轴交点的个数
研究函数图象
【思路2】
判断函数零点个数的思路
二次函数零点
一元二次方程的解
研究函
数图象
单调性、端点值符号
确定零点
零点存在定理
抛物线的对称轴和开口方向
思考探究
思考探究
判断函数 是否存在零点.
【思路1】
函数零点
函数图象交点
方程的解
方程转化
为函数
函数转化
为方程
思考探究
【思路2】
正确求导
确定导数
符号
确定函数零点个数
确定函数单调性
确定某些点函数值
有且仅有1个零点
判断函数 是否存在零点.
思考探究
没有零点
判断函数 在区间 内是否存在零点.
思考探究
变式:判断函数 在 上零点的个数.
有没有零点?
思考探究
判断函数 在 上零点的个数.
【思路】
,定义域 ,
令 ,可解得 ,
当 x 变化时, 、 的变化情况如下表:
极小值
-1
典例分析
方法1:函数零点转化为方程的解,进而转化为曲线交点.
方法2:研究函数图象与 轴公共点的个数.
【思考】如何判断函数在所给区间内是否存在极值?
函数存在极值
导函数存在
变号的零点
构造新函数
利用导数研究新函数单调性
确定单调区间及单调区间内某些点函数值的符号
研究函数存在极值的解题思路
题后反思
1.正确求导是解决问题的关键.
2.决定导数符号有正负变化的是导数的零点.
3.适时构造新函数.
4.零点存在定理的应用.
回顾反思
1.本节课我们主要研究了什么样的问题?
2.解决此类问题的方法是什么?有什么样的体会?
3.在解决问题过程中,运用了哪些数学思想和方法?
回顾反思
函数的零点问题
函数图象的交点
方程的解
图象与 轴公共点
利用导数研究函数的零点的一般方法和步骤:
明确函数及其定义域
求导函数
判断 的符号
研究 单调性
借助零点存在定理
函数图象
函数零点
研究 极值
研究区间端点值
多角度思考,重视一题多解,体会解法特点,积累解题经验,提高方法识别与选择的能力.
55
回顾反思
函数与方程、函数与不等式、数与形、转化与化归、数形结合、分类与整合……
注重对问题的深入分析和思维训练、分析求解条件、探求求解方向、确定求解思路.
课后作业
