高中数学人教A版选修2-2 利用导数解决综合问题(1) 课件(95张ppt)
文档属性
| 名称 | 高中数学人教A版选修2-2 利用导数解决综合问题(1) 课件(95张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:19:20 | ||
图片预览










文档简介
(共95张PPT)
高二年级 数学
利用导数解决综合问题(1)
知 识 回 顾
1.如何利用导数求切线的斜率?
2
知 识 回 顾
1.如何利用导数求切线的斜率?
3
设切点为
在M点处的切线斜率为:
在点
【练习1】已知函数
(k为常数),曲线
处的切线与x轴平行.则实数
k的值为
在点
所以
又由题知
【练习1】已知函数
(k为常数),曲线
处的切线与x轴平行.则实数
k的值为
解:
知 识 回 顾
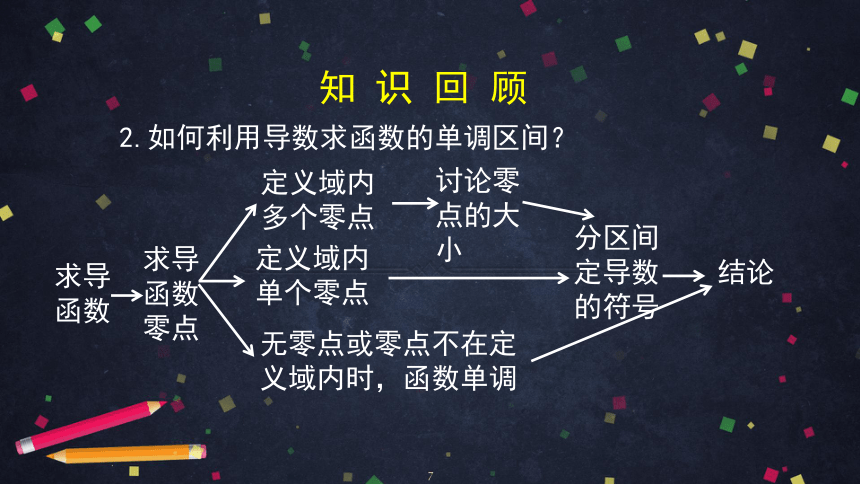
2.如何利用导数求函数的单调区间?
6
知 识 回 顾
2.如何利用导数求函数的单调区间?
7
求导函数
求导函数零点
定义域内单个零点
无零点或零点不在定义域内时,函数单调
分区间定导数的符号
结论
定义域内多个零点
讨论零点的大小
【练习2】若函数
在区间
上单调
递增,则k的取值范围是( )
【练习2】若函数
在区间
上单调
递增,则k的取值范围是( )
解:因为
所以
因为
在区间
上单调递增,
.
所以当
时,
恒成立,
在区间
上恒成立.
即
所以
所以
因为
故选D.
,
,
知 识 回 顾
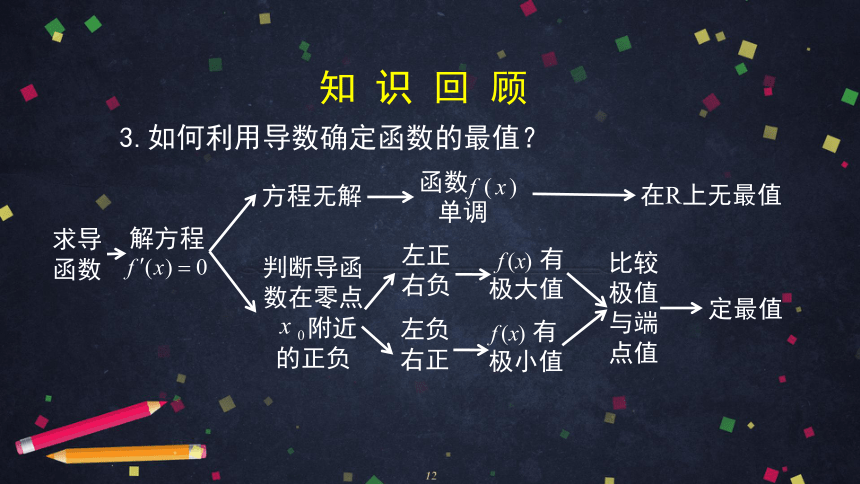
3.如何利用导数确定函数的最值?
11
知 识 回 顾
3.如何利用导数确定函数的最值?
12
求导函数
解方程
函数
单调
方程无解
在R上无最值
判断导函数在零点
附近的正负
有
极小值
左正
右负
左负
右正
有
极大值
比较极值与端点值
定最值
【练习3】若函数
在区间
上存在最小值,实数a的取值范围是( )
【练习3】若函数
在区间
上存在最小值,实数a的取值范围是( )
解:由题意,得
【练习3】若函数
在区间
解:由题意,得
故
在
上是增函数,
上存在最小值,实数a的取值范围是( )
作出其图象如图所示,
解得
得
则结合图象可知,
故选C.
小结:
(1)求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小.
(2)求函数在无穷区间(或开区间)上的最值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图象,然后借助图象观察得到函数的最值.
几何表述
几何表述
代数表述
设
就是要证
在 上恒成立
在 上恒成立
?
还是
?
在 上恒成立
?
还是
?
在 上恒成立
√
?
还是
?
几何表述
代数表述
设
就是要证
在 上恒成立.
令
即要证
如何判断符号?
退
退
退
(舍)
,
,
,
,
,
当 时,
当 时,
在 上单调递增,
在 上单调递减.
即 ,
,所以
,所以
在 处取得最大值 .
所以
所以 时, ,
所以 ,
所以除切点(1,0)之外,曲线C在直线l的下方. ,
小结:
(1)一般地,曲线的位置关系问题常可以转化为不等式恒成立问题,而不等式恒成立问题又可以转化为最值(或值域)问题借助导数处理.在转化时不仅要知其然,更要知其所以然;
(2)在求导以后如果出现超越方程,我们可以考虑能否通过“去分母”等手段规避超越方程.
退
退
解法2:
当 时,
当 时,
在 上单调递增,
在 上单调递减.
所以
所以
,
所以
,
,
,
,
所以
,
在 处取得最大值 .
所以
所以 ,即 ,
所以 时, ,
所以除切点(1,0)之外,曲线C在直线l的下方. ,
退
退
解法3:
在 上单调递减
在 上单调递增,
当 时,
在 上单调递减.
所以
所以
所以
所以
,
,
,
,
,
,
,
,
令 , ,
所以 时,
即
所以
,
,
,
在 处取得最大值 .
所以
小结:
对于求导以后出现方程不易求解的问题,我们可以尝试通过“数形结合”做出直观判断,再借助“二次求导”进行代数处理.
【例2】已知函数 ,求函数 在
在区间 上的最大值和最小值.
?
【例2】已知函数 ,求函数 在
在区间 上的最大值和最小值.
构建函数
解法1:
,
,
,
【例2】已知函数 ,求函数 在
在区间 上的最大值和最小值.
所以
由已知得
小结:
利用导数研究函数 的形态,探究函数 的值域,进而判断函数 的单调性.
构建函数
构建函数
构建函数
构建函数
解法2:
,
,
,
,
再次构建函数
,
所以 , .
所以 在区间 上单调递减.
综上, 在区间 上单调递减.
构建函数
小结:
观察函数的解析式,从所熟悉的 入手,用三角函数辅助角公式化简后求解.当导函数的正负直接判断有困难时,继续构建函数求解.
构建函数
构建函数
解法3:
,
,
,
解法3:
,
,
,
解法3:
,
,
,
所以 ,
因为 ,所以 ,
所以 ,
又因为 ,所以 ,
所以 在区间 上单调递减.
所以 ,
所以 ,
所以 在区间 上单调递减.
所以 , .
总结:
应用导数研究函数一般要经过哪几个环节?
总结:
应用导数研究函数一般要经过哪几个环节?
分析问题
构建函数
研究函数
解决问题
总结:
应用导数研究函数一般要经过哪几个环节?
分析问题
构建函数
研究函数
解决问题
难点!
----多观察
多思考
多尝试
多积累
【例3】已知函数 , .
(1)求证: ;
(2)若在 上 恒成立,求a的最大
值与b的最小值.
思路分析:
【例3】已知函数 , .
(1)求证: ;
解:(1)由 ,
得
,
因为在区间 上 ,
所以 在区间 上单调递减.
从而 .
(2)若在 上 恒成立,求a的最大
值与b的最小值.
【例3】已知函数 , .
,
解析:
故函数
在区间
内单调递减,
从而
的最小值为 .
令 , ,
则
,由(1)知 ,
故
,a的最大值为 .
,
,
故
,a的最大值为
如何求b的最小值?
,
,
等价于
因为
不符合题意.
,
,
,
,
,
符合题意.
故函数
在区间
内单调递减
,
,
,
,
,
,
有根吗?
有几个?
,
有根吗?
有几个?
我们可以二次求导:
,
有根吗?
有几个?
我们可以二次求导:
在区间
内单调递减.
,
,
.
有根吗?
有几个?
我们可以二次求导:
在区间
内单调递减.
内一定有根!
,
,
.
于是,存在唯一的
且当
时
单调递增,
函数
当
时
单调递减,
函数
不符合题意.
综上,b 的最小值为1.
,
,
,
,
所以,若 在 上恒成立,
a的最大值为 ,b的最小值为1.
总结:当方程有根,但无法用已知字母或数字表示时,可以设这个根为x0(隐性零点),则x0满足方程 .
此题中
,方程
没有用到,
一般地,
又由
得 .
,
,
所以
,由(1)知,
,不符合题意.
从概念出发!
思考:(2)中的难点:
当 时,
导数概念的形式化定义:
它的等价形式是:
(2)解法2:令
所以
在
上单调递减,
所以
,
,得
因为
综上所述,
的最大值为
所以
b的最小值为1.
,
,
总结:将
与导数的概念联系起来,顺利求出了函数的极限.
转化为
加强对导数概念的理解与运用!
,
课堂小结:
1.解决函数导数问题一般要经历四个环节
分析问题
构建函数
研究函数
解决问题
2.对导数的认识
导函数也是函数,是刻画函数的重要概念、函数性质学习的延续;
是研究函数性质的重要工具,是研究可导函数性质的通用方法;
是考查函数与方程、分类讨论、转化与化归等数学思想方法的重要载体;
是函数与方程、不等式等有关知识的交汇点可以考查综合运用所学知识的能力.
作 业
高二年级 数学
利用导数解决综合问题(1)
知 识 回 顾
1.如何利用导数求切线的斜率?
2
知 识 回 顾
1.如何利用导数求切线的斜率?
3
设切点为
在M点处的切线斜率为:
在点
【练习1】已知函数
(k为常数),曲线
处的切线与x轴平行.则实数
k的值为
在点
所以
又由题知
【练习1】已知函数
(k为常数),曲线
处的切线与x轴平行.则实数
k的值为
解:
知 识 回 顾
2.如何利用导数求函数的单调区间?
6
知 识 回 顾
2.如何利用导数求函数的单调区间?
7
求导函数
求导函数零点
定义域内单个零点
无零点或零点不在定义域内时,函数单调
分区间定导数的符号
结论
定义域内多个零点
讨论零点的大小
【练习2】若函数
在区间
上单调
递增,则k的取值范围是( )
【练习2】若函数
在区间
上单调
递增,则k的取值范围是( )
解:因为
所以
因为
在区间
上单调递增,
.
所以当
时,
恒成立,
在区间
上恒成立.
即
所以
所以
因为
故选D.
,
,
知 识 回 顾
3.如何利用导数确定函数的最值?
11
知 识 回 顾
3.如何利用导数确定函数的最值?
12
求导函数
解方程
函数
单调
方程无解
在R上无最值
判断导函数在零点
附近的正负
有
极小值
左正
右负
左负
右正
有
极大值
比较极值与端点值
定最值
【练习3】若函数
在区间
上存在最小值,实数a的取值范围是( )
【练习3】若函数
在区间
上存在最小值,实数a的取值范围是( )
解:由题意,得
【练习3】若函数
在区间
解:由题意,得
故
在
上是增函数,
上存在最小值,实数a的取值范围是( )
作出其图象如图所示,
解得
得
则结合图象可知,
故选C.
小结:
(1)求极值、最值时,要求步骤规范,含参数时,要讨论参数的大小.
(2)求函数在无穷区间(或开区间)上的最值,不仅要研究其极值情况,还要研究其单调性,并通过单调性和极值情况,画出函数的大致图象,然后借助图象观察得到函数的最值.
几何表述
几何表述
代数表述
设
就是要证
在 上恒成立
在 上恒成立
?
还是
?
在 上恒成立
?
还是
?
在 上恒成立
√
?
还是
?
几何表述
代数表述
设
就是要证
在 上恒成立.
令
即要证
如何判断符号?
退
退
退
(舍)
,
,
,
,
,
当 时,
当 时,
在 上单调递增,
在 上单调递减.
即 ,
,所以
,所以
在 处取得最大值 .
所以
所以 时, ,
所以 ,
所以除切点(1,0)之外,曲线C在直线l的下方. ,
小结:
(1)一般地,曲线的位置关系问题常可以转化为不等式恒成立问题,而不等式恒成立问题又可以转化为最值(或值域)问题借助导数处理.在转化时不仅要知其然,更要知其所以然;
(2)在求导以后如果出现超越方程,我们可以考虑能否通过“去分母”等手段规避超越方程.
退
退
解法2:
当 时,
当 时,
在 上单调递增,
在 上单调递减.
所以
所以
,
所以
,
,
,
,
所以
,
在 处取得最大值 .
所以
所以 ,即 ,
所以 时, ,
所以除切点(1,0)之外,曲线C在直线l的下方. ,
退
退
解法3:
在 上单调递减
在 上单调递增,
当 时,
在 上单调递减.
所以
所以
所以
所以
,
,
,
,
,
,
,
,
令 , ,
所以 时,
即
所以
,
,
,
在 处取得最大值 .
所以
小结:
对于求导以后出现方程不易求解的问题,我们可以尝试通过“数形结合”做出直观判断,再借助“二次求导”进行代数处理.
【例2】已知函数 ,求函数 在
在区间 上的最大值和最小值.
?
【例2】已知函数 ,求函数 在
在区间 上的最大值和最小值.
构建函数
解法1:
,
,
,
【例2】已知函数 ,求函数 在
在区间 上的最大值和最小值.
所以
由已知得
小结:
利用导数研究函数 的形态,探究函数 的值域,进而判断函数 的单调性.
构建函数
构建函数
构建函数
构建函数
解法2:
,
,
,
,
再次构建函数
,
所以 , .
所以 在区间 上单调递减.
综上, 在区间 上单调递减.
构建函数
小结:
观察函数的解析式,从所熟悉的 入手,用三角函数辅助角公式化简后求解.当导函数的正负直接判断有困难时,继续构建函数求解.
构建函数
构建函数
解法3:
,
,
,
解法3:
,
,
,
解法3:
,
,
,
所以 ,
因为 ,所以 ,
所以 ,
又因为 ,所以 ,
所以 在区间 上单调递减.
所以 ,
所以 ,
所以 在区间 上单调递减.
所以 , .
总结:
应用导数研究函数一般要经过哪几个环节?
总结:
应用导数研究函数一般要经过哪几个环节?
分析问题
构建函数
研究函数
解决问题
总结:
应用导数研究函数一般要经过哪几个环节?
分析问题
构建函数
研究函数
解决问题
难点!
----多观察
多思考
多尝试
多积累
【例3】已知函数 , .
(1)求证: ;
(2)若在 上 恒成立,求a的最大
值与b的最小值.
思路分析:
【例3】已知函数 , .
(1)求证: ;
解:(1)由 ,
得
,
因为在区间 上 ,
所以 在区间 上单调递减.
从而 .
(2)若在 上 恒成立,求a的最大
值与b的最小值.
【例3】已知函数 , .
,
解析:
故函数
在区间
内单调递减,
从而
的最小值为 .
令 , ,
则
,由(1)知 ,
故
,a的最大值为 .
,
,
故
,a的最大值为
如何求b的最小值?
,
,
等价于
因为
不符合题意.
,
,
,
,
,
符合题意.
故函数
在区间
内单调递减
,
,
,
,
,
,
有根吗?
有几个?
,
有根吗?
有几个?
我们可以二次求导:
,
有根吗?
有几个?
我们可以二次求导:
在区间
内单调递减.
,
,
.
有根吗?
有几个?
我们可以二次求导:
在区间
内单调递减.
内一定有根!
,
,
.
于是,存在唯一的
且当
时
单调递增,
函数
当
时
单调递减,
函数
不符合题意.
综上,b 的最小值为1.
,
,
,
,
所以,若 在 上恒成立,
a的最大值为 ,b的最小值为1.
总结:当方程有根,但无法用已知字母或数字表示时,可以设这个根为x0(隐性零点),则x0满足方程 .
此题中
,方程
没有用到,
一般地,
又由
得 .
,
,
所以
,由(1)知,
,不符合题意.
从概念出发!
思考:(2)中的难点:
当 时,
导数概念的形式化定义:
它的等价形式是:
(2)解法2:令
所以
在
上单调递减,
所以
,
,得
因为
综上所述,
的最大值为
所以
b的最小值为1.
,
,
总结:将
与导数的概念联系起来,顺利求出了函数的极限.
转化为
加强对导数概念的理解与运用!
,
课堂小结:
1.解决函数导数问题一般要经历四个环节
分析问题
构建函数
研究函数
解决问题
2.对导数的认识
导函数也是函数,是刻画函数的重要概念、函数性质学习的延续;
是研究函数性质的重要工具,是研究可导函数性质的通用方法;
是考查函数与方程、分类讨论、转化与化归等数学思想方法的重要载体;
是函数与方程、不等式等有关知识的交汇点可以考查综合运用所学知识的能力.
作 业
