高中数学人教B版选修1-1 利用导数判断函数的单调性(2) 课件(47张ppt)
文档属性
| 名称 | 高中数学人教B版选修1-1 利用导数判断函数的单调性(2) 课件(47张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览









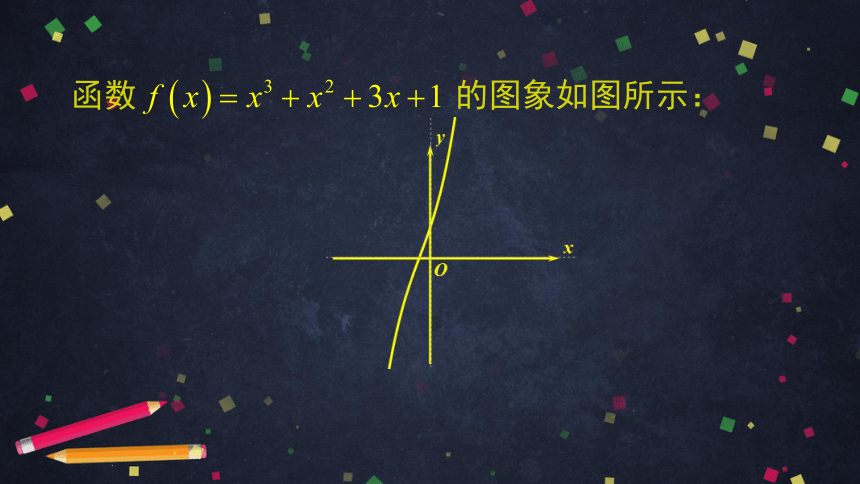

文档简介
(共47张PPT)
高二年级 数学
利用导数判断函数的单调性(2)
若 在某个区间 内可导,则
对 有 在 上单调递增;
对 有 在 上单调递减.
【问题1】请同学们回顾函数的单调性和导数的关系.
【问题2】请同学们回顾用“导数法”求函数单调区间的步骤.
(1)确定函数 的定义域;
(2)求出函数 的导数 ;
(3)在定义域内解不等式 或 ;
(4)下结论,确定函数 的单调区间.
【问题3】已知函数 ,确定函数
的单调区间.
解:
令
解此不等式,得 或 .
因此, 在区间 和 内是增函数.
【问题3】已知函数 ,确定函数
的单调区间.
解:
令
解此不等式,得 .
因此, 在区间 内是减函数.
函数 的图象如图所示:
【问题4】已知函数 ,确定函数
的单调区间.
解:
令
解此不等式,得 .
因此, 在区间 内是增函数.
解:
令
【问题4】已知函数 ,确定函数
的单调区间.
解此不等式,得 或 .
因此, 在区间 和 内是减函数.
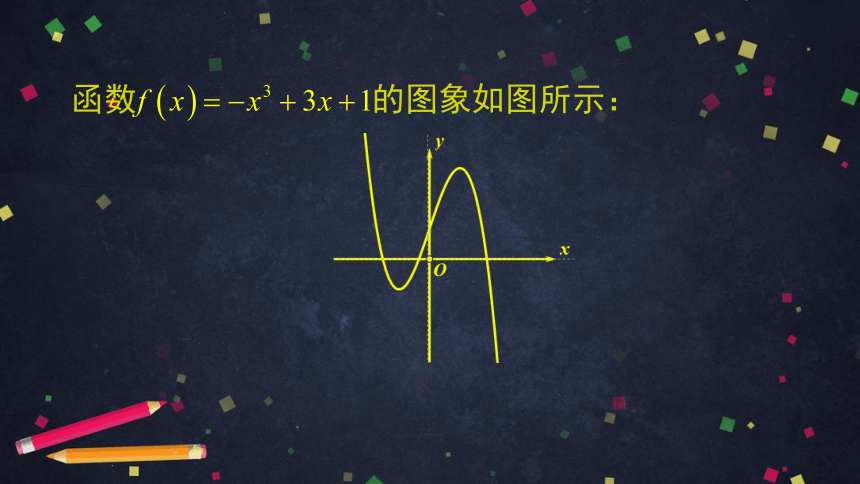
函数 的图象如图所示:
【问题5】已知函数 ,确定函数 的单调区间.
解: 恒成立,
因此, 在 上单调递增.
函数 的图象如图所示:
【问题6】已知函数 ,确定函数 的单调区间.
解:
恒成立,
因此, 在 上单调递减.
函数 的图象如图所示:
【问题7】已知函数 ,确定函数 的单调区间.
解:
令 解得 或 .
(1)当 时, , 恒成立,
所以 在 上单调递增.
(2)当 时, ,
令 ,解得 或 ,
令 ,解得 ,
所以 的递增区间为 和 ,单调递减区间为 .
(3)当 时, ,
令 ,解得 或 ,
令 ,解得 ,
所以 的递增区间为 和 ,单调递减区间为 .
综上所述:
(1) 当 时, 在 上单调递增.
(2) 当 时, 的单调递增区间为 和
,单调递减区间为 .
(3) 当 时, 的单调递增区间为 和 和 ,单调递减区间为 .
函数 的图象如图所示:
【问题8】已知函数 ,确定函数
的单调区间.
解:
(1)当 时, 恒成立,
所以 在 上单调递减.
【问题8】已知函数 ,确定函数
的单调区间.
解:
(2)当 时, 恒成立,
所以 在 上单调递减.
(3)当 时, ,
令 ,解得 或 ,
所以 的递增区间为 和 .
(3)当 时, ,
令 ,解得 ,
所以 的递减区间为 .
综上所述:
(1) 当 时, 在 上单调递减.
(2) 当 时, 的单调递增区间为
和 ,单调递减区间为 .
函数 的图象如图所示:
【问题9】已知函数 的单调递减区间为 ,求实数 的值.
解:函数 的单调递减区间就是 的解集,
由问题8可知:
(1) 当 时, 在 上单调递减.这与函数 的单调递减区间为 矛盾,不符合题意.
【问题9】已知函数 的单调递减区间为 ,求实数 的值.
(2) 当 时, 的单调递减区间为 ,
即为 ,所以 ,解得 ,经检验符合题意.
综合(1)、(2)知: 的值为 .
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
解:方法1:由问题8可知:
(1) 当 时, 在 上单调递减.显然满足区间 上单调递减,所以 符合题意.
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
(2) 当 时, 的单调递减区间为 ,
所以区间 为 的子区间,即 ,
解得 .
综合(1)、(2)知: 的取值范围为 .
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
解:方法2:由题意可知, 对任意
恒成立.
当 时, 显然恒成立,所以
满足题意.
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
(2)当 时, 恒成立,问题等价
于 ,解得 .
综合(1)、(2)知: 的取值范围为 .
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
解:方法3:由题意可知, 对任意
恒成立.
当 时, 显然恒成立,所以 .
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
(2)当 时,不等式等价于 对任意的
恒成立,即 .
综合(1)、(2)知: 的取值范围为 .
【问题11】已知函数 在区间
上不单调,求实数 的取值范围.
解:当 时, 显然恒成立,这与
在区间 上不单调矛盾,所以 舍去.
当 时,因为 在区间 不单调,所以
必有 ,即 .
【问题12】已知函数 在区间
上存在单调增区间,求实数 的取值范围.
解:当 时, 显然恒成立,
在区间 单调递减,显然矛盾,所以 舍去.
当 时,问题等价于 在 有解,
,即 .
【问题13】请同学们尝试确定一元三次函数
的单调区间.
解: ,方程 的判别式为
.
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间: .
递减区间: .
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间: .
递减区间:无.
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间: .
递减区间:无.
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递减区间: .
递增区间: .
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间:无.
递减区间: .
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间:无.
递减区间: .
1.一般三次函数的图象特征:
【问题14】通过本节课的学习,你有什么收获?
图象分为两大类:
一类是当 时,图象上升趋势,当
时,函数图象只有一个单调递增区间;当 时,函数图象有两个递增区间一个递减区间.
1.一般三次函数的图象特征:
【问题14】通过本节课的学习,你有什么收获?
图象分为两大类:
一类是当 时,图象下降趋势,当
时,函数图象只有一个单调递减区间;当 时,函数图象有两个递减区间一个递增区间.
2.含参三次函数的单调区间求解策略:
①当二次项系数含有参数时,首先要对二次项系数进行讨论;
②当二次项系数为常数,但不知道与之对应的一元二次方程是否有解时,需要对判别式△进行讨论;
③当二次项系数为常数,且与之对应的一元二次方程有两解时,需要对解的大小进行比较.
【问题14】通过本节课的学习,你有什么收获?
3.本节课体现的数学思想方法:
化归转化思想:梳理单调性、最值、恒成立问题如何相互转化,其基础是导数,根本是单调性的研究.
分类讨论思想:总结参数讨论的基本依据与方法.
数形结合思想:体会由数想形,由形助数.
基础作业:
一、讨论函数 的单调性.
拓展作业:
二、求证:当 时, .
谢谢!
高二年级 数学
利用导数判断函数的单调性(2)
若 在某个区间 内可导,则
对 有 在 上单调递增;
对 有 在 上单调递减.
【问题1】请同学们回顾函数的单调性和导数的关系.
【问题2】请同学们回顾用“导数法”求函数单调区间的步骤.
(1)确定函数 的定义域;
(2)求出函数 的导数 ;
(3)在定义域内解不等式 或 ;
(4)下结论,确定函数 的单调区间.
【问题3】已知函数 ,确定函数
的单调区间.
解:
令
解此不等式,得 或 .
因此, 在区间 和 内是增函数.
【问题3】已知函数 ,确定函数
的单调区间.
解:
令
解此不等式,得 .
因此, 在区间 内是减函数.
函数 的图象如图所示:
【问题4】已知函数 ,确定函数
的单调区间.
解:
令
解此不等式,得 .
因此, 在区间 内是增函数.
解:
令
【问题4】已知函数 ,确定函数
的单调区间.
解此不等式,得 或 .
因此, 在区间 和 内是减函数.
函数 的图象如图所示:
【问题5】已知函数 ,确定函数 的单调区间.
解: 恒成立,
因此, 在 上单调递增.
函数 的图象如图所示:
【问题6】已知函数 ,确定函数 的单调区间.
解:
恒成立,
因此, 在 上单调递减.
函数 的图象如图所示:
【问题7】已知函数 ,确定函数 的单调区间.
解:
令 解得 或 .
(1)当 时, , 恒成立,
所以 在 上单调递增.
(2)当 时, ,
令 ,解得 或 ,
令 ,解得 ,
所以 的递增区间为 和 ,单调递减区间为 .
(3)当 时, ,
令 ,解得 或 ,
令 ,解得 ,
所以 的递增区间为 和 ,单调递减区间为 .
综上所述:
(1) 当 时, 在 上单调递增.
(2) 当 时, 的单调递增区间为 和
,单调递减区间为 .
(3) 当 时, 的单调递增区间为 和 和 ,单调递减区间为 .
函数 的图象如图所示:
【问题8】已知函数 ,确定函数
的单调区间.
解:
(1)当 时, 恒成立,
所以 在 上单调递减.
【问题8】已知函数 ,确定函数
的单调区间.
解:
(2)当 时, 恒成立,
所以 在 上单调递减.
(3)当 时, ,
令 ,解得 或 ,
所以 的递增区间为 和 .
(3)当 时, ,
令 ,解得 ,
所以 的递减区间为 .
综上所述:
(1) 当 时, 在 上单调递减.
(2) 当 时, 的单调递增区间为
和 ,单调递减区间为 .
函数 的图象如图所示:
【问题9】已知函数 的单调递减区间为 ,求实数 的值.
解:函数 的单调递减区间就是 的解集,
由问题8可知:
(1) 当 时, 在 上单调递减.这与函数 的单调递减区间为 矛盾,不符合题意.
【问题9】已知函数 的单调递减区间为 ,求实数 的值.
(2) 当 时, 的单调递减区间为 ,
即为 ,所以 ,解得 ,经检验符合题意.
综合(1)、(2)知: 的值为 .
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
解:方法1:由问题8可知:
(1) 当 时, 在 上单调递减.显然满足区间 上单调递减,所以 符合题意.
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
(2) 当 时, 的单调递减区间为 ,
所以区间 为 的子区间,即 ,
解得 .
综合(1)、(2)知: 的取值范围为 .
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
解:方法2:由题意可知, 对任意
恒成立.
当 时, 显然恒成立,所以
满足题意.
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
(2)当 时, 恒成立,问题等价
于 ,解得 .
综合(1)、(2)知: 的取值范围为 .
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
解:方法3:由题意可知, 对任意
恒成立.
当 时, 显然恒成立,所以 .
【问题10】已知函数 在区间
上单调递减,求实数 的取值范围.
(2)当 时,不等式等价于 对任意的
恒成立,即 .
综合(1)、(2)知: 的取值范围为 .
【问题11】已知函数 在区间
上不单调,求实数 的取值范围.
解:当 时, 显然恒成立,这与
在区间 上不单调矛盾,所以 舍去.
当 时,因为 在区间 不单调,所以
必有 ,即 .
【问题12】已知函数 在区间
上存在单调增区间,求实数 的取值范围.
解:当 时, 显然恒成立,
在区间 单调递减,显然矛盾,所以 舍去.
当 时,问题等价于 在 有解,
,即 .
【问题13】请同学们尝试确定一元三次函数
的单调区间.
解: ,方程 的判别式为
.
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间: .
递减区间: .
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间: .
递减区间:无.
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间: .
递减区间:无.
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递减区间: .
递增区间: .
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间:无.
递减区间: .
【问题13】请同学们尝试确定一元三次函数
的单调区间.
递增区间:无.
递减区间: .
1.一般三次函数的图象特征:
【问题14】通过本节课的学习,你有什么收获?
图象分为两大类:
一类是当 时,图象上升趋势,当
时,函数图象只有一个单调递增区间;当 时,函数图象有两个递增区间一个递减区间.
1.一般三次函数的图象特征:
【问题14】通过本节课的学习,你有什么收获?
图象分为两大类:
一类是当 时,图象下降趋势,当
时,函数图象只有一个单调递减区间;当 时,函数图象有两个递减区间一个递增区间.
2.含参三次函数的单调区间求解策略:
①当二次项系数含有参数时,首先要对二次项系数进行讨论;
②当二次项系数为常数,但不知道与之对应的一元二次方程是否有解时,需要对判别式△进行讨论;
③当二次项系数为常数,且与之对应的一元二次方程有两解时,需要对解的大小进行比较.
【问题14】通过本节课的学习,你有什么收获?
3.本节课体现的数学思想方法:
化归转化思想:梳理单调性、最值、恒成立问题如何相互转化,其基础是导数,根本是单调性的研究.
分类讨论思想:总结参数讨论的基本依据与方法.
数形结合思想:体会由数想形,由形助数.
基础作业:
一、讨论函数 的单调性.
拓展作业:
二、求证:当 时, .
谢谢!
