沪科版九年级下册数学课件 :24.4 直线与圆的位置关系第二课时(共28张PPT)
文档属性
| 名称 | 沪科版九年级下册数学课件 :24.4 直线与圆的位置关系第二课时(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
24.4 直线与圆的位置关系(2)
切线的判定
下雨天转动雨伞时飞出的水,以及在砂轮上打磨工件飞出的火星,均沿着圆的切线的方向飞出.
1、当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2、砂轮打磨零件飞出火星的方向是什么方向?
情景导入
如何判定一条直线是已知圆的切线?
(1)与圆只有一个公共点的直线是圆的切线;
还有其它方法吗?
操作
过圆O内一点作直线,这条直线与圆有什么位置关系?过半径OA上一点(A除外)能作圆O的切线吗?过点A呢?
r
l
动手试一试!
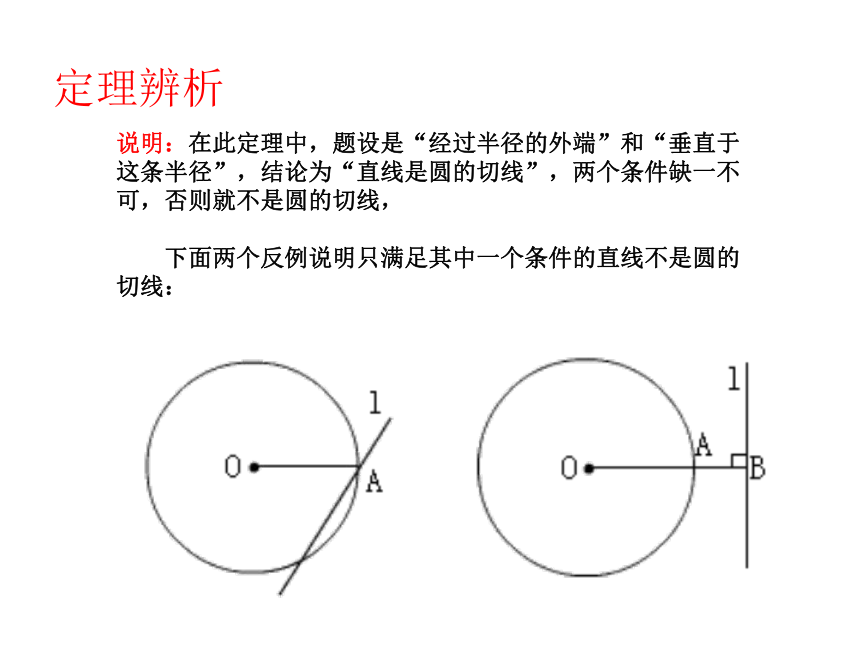
经过半径的外端点并且垂直于这条半径的直线是圆的切线。
条件:
(1)经过半径的外端;
圆的切线判定定理:
(2)垂直于过该点半径。
┐
A
l
∵l⊥OA,且l 经过⊙O上的A点
∴直线l是⊙O的切线
符号语言表达
定理辨析
如何判定一条直线是已知圆的切线?
(1)与圆只有一个公共点的直线是圆的切线;
(2)到圆心的距离等于半径的直线是圆的
切线;
(3)过半径外端点且和半径垂直的直线
是圆的切线。——切线判定定理
(d=r)
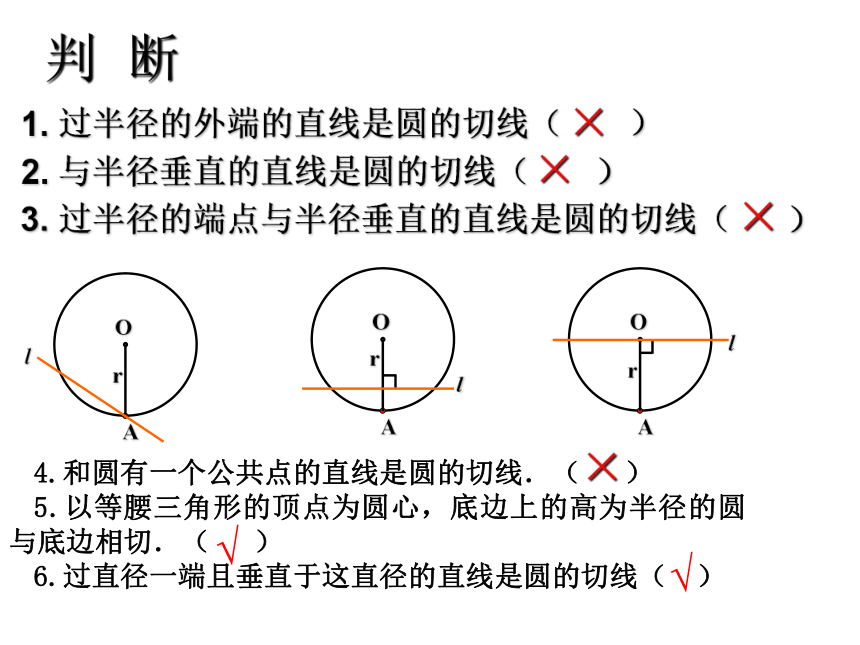
判 断
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
4.和圆有一个公共点的直线是圆的切线.( )
5.以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
6.过直径一端且垂直于这直径的直线是圆的切线( )
×
√
√
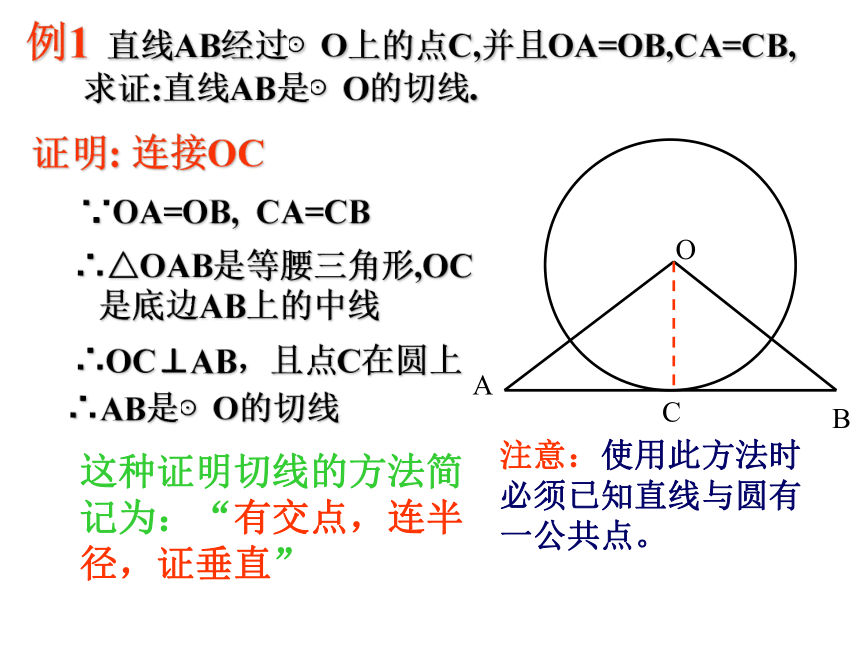
例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
证明: 连接OC
∵OA=OB, CA=CB
∴△OAB是等腰三角形,OC
是底边AB上的中线
∴OC⊥AB,且点C在圆上
∴AB是⊙O的切线
O
C
B
A
这种证明切线的方法简记为:“有交点,连半径,证垂直”
注意:使用此方法时必须已知直线与圆有一公共点。
练习1、如图,AB是⊙O的直径,∠ABC=45°,AC=AB,AC是⊙O的切线吗?为什么?
解:∵AB=AC ∴∠ACB=∠ABC=450 ∴∠BAC=900 即AB⊥AC ∵ AB是⊙O的直径 ∴ AC是⊙O的切线
变式练习
练习2、如图:线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B = 30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
解:BD是⊙O的切线
连接OD ∵ OD=OA ∴∠ODA=∠BAD=∠B=300 ∴∠ BOD=600 ∴∠ODB=900 即:OD⊥DB 且点O在圆上
∴BD是⊙O的切线
变式练习
证明:连结OP。
∵ AB为直径
∴ OB=OA,BP=PC,
∴OP∥AC。
又∵ PE⊥AC,
∴PE⊥OP,且点P在圆上
∴PE为⊙0的切线。
练习3,△ABC中,以AB为直径的⊙O,交边BC于P, BP=PC, PE⊥AC于E。
求证:PE是⊙O的切线。
变式练习
例2:已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
D
证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。
与例1比较,你发现了什么?
已知如图,△ABC为等腰三角形,O是底边BC的中点,⊙O与腰AB相切于点D。AC与⊙O相切吗?为什么?
E
解:AC与⊙O相切 连接OD,作OE⊥AC ∴∠OEC=900 ∵ AB是⊙O的切线∴OD⊥AB, ∴∠ODB=900=∠OEC ∵AB=AC ∴∠B=∠C ∵O是BC的中点∴OB=OC ∴△OBD≌△OCE ∴OD=OE ∴AC与⊙O相切
无交点,作垂直,证半径
小 结
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:知交点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:无交点,作垂直,证半径。
例3 如图,AB是⊙O的直径, C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D. 求证:AC平分∠DAB.
证明:连接OC.
∵CD 是⊙O的切线,
∴OC⊥CD.
又∵AD⊥CD , ∴OC//AD.
∴∠ACO= ∠CAD .
又∵OC=OA,
∴∠CAO= ∠ACO
∴∠CAD= ∠CAO ,
故AC平分∠DAB.
圆心与切点的连线是常添的辅助线!
1, 如图:AC是⊙O的切线,∠B=600。求∠CAD= 。
C
2,如图:以O为圆心的同心圆,大圆的弦AB是小圆的切线,C是切点,求证:C是AB的中点。
课堂小结
1. 判定切线的方法有哪些?
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2.常用的添辅助线方法?
⑴直线与圆的公共点已知时,作出过公共点的半径,
再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线
段,再证明这条垂线段等于圆的半径。(作垂直,证半径)
l是圆的切线
l是圆的切线
3.圆的切线性质定理:圆的切线垂直于圆的半径。
辅助线作法:连接圆心与切点可得半径与切线垂直。即“连半径,得垂直”。
1、已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.
求证:DC是⊙O的切线.
证明:连结OD.
∵OA=OD,∴∠1=∠2,
∵AD∥OC,∴∠1=∠3、∠2=∠4
∴∠3=∠4
在△OBC和△ODC中,
OB=OD,∠3=∠4,OC=OC ,
∴△OBC≌△ODC,∴∠OBC=∠ODC
∵BC是⊙O的切线,∴∠OBC=90°,∴∠ODC=90°.
∴DC是⊙O的切线.
2、求证:如果圆的两条切线互相平行,则连结两个切点的线段是直径。
已知:AB、CD是⊙O的两条切线,E、F为切点,且AB∥CD
求证:连结E、F的线段是直径。
证明:连结EO并延长
∵AB切⊙O于E,∴OE⊥AB,
∵AB∥CD,∴OE⊥CD.
∵CD是⊙O切线,F为切点,∴OE必过切点F
∴EF为⊙O直径
3、如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,
求证:CD与小圆相切
证明:连结OE,过O作OF⊥CD,垂足为F
∵AB与小圆O切于点点E,∴OE⊥AB.
又∵AB=CD,
∴OF=OE,又OF⊥CD,
∴CD与小圆O相切.
4、已知:AB是半⊙O直径,CD⊥AB于D,EC是切线,E为切点
求证:CE=CF
证明:连结OE
∵BE=BO∴∠3=∠B
∵CE切⊙O于E
∴OE⊥CE? ∠2+∠3=90°
∵CD⊥AB? ∴∠4+∠B=90°
∴∠2=∠4
∵∠1=∠4? ∴∠1=∠2
∴CE=CF
作业:
1、阅读教材P35-36
2、P36练习第1、2、3题
3、选做基础训练24.4部分习题
相信自己
再见!
24.4 直线与圆的位置关系(2)
切线的判定
下雨天转动雨伞时飞出的水,以及在砂轮上打磨工件飞出的火星,均沿着圆的切线的方向飞出.
1、当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2、砂轮打磨零件飞出火星的方向是什么方向?
情景导入
如何判定一条直线是已知圆的切线?
(1)与圆只有一个公共点的直线是圆的切线;
还有其它方法吗?
操作
过圆O内一点作直线,这条直线与圆有什么位置关系?过半径OA上一点(A除外)能作圆O的切线吗?过点A呢?
r
l
动手试一试!
经过半径的外端点并且垂直于这条半径的直线是圆的切线。
条件:
(1)经过半径的外端;
圆的切线判定定理:
(2)垂直于过该点半径。
┐
A
l
∵l⊥OA,且l 经过⊙O上的A点
∴直线l是⊙O的切线
符号语言表达
定理辨析
如何判定一条直线是已知圆的切线?
(1)与圆只有一个公共点的直线是圆的切线;
(2)到圆心的距离等于半径的直线是圆的
切线;
(3)过半径外端点且和半径垂直的直线
是圆的切线。——切线判定定理
(d=r)
判 断
1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )
×
×
×
4.和圆有一个公共点的直线是圆的切线.( )
5.以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
6.过直径一端且垂直于这直径的直线是圆的切线( )
×
√
√
例1 直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
证明: 连接OC
∵OA=OB, CA=CB
∴△OAB是等腰三角形,OC
是底边AB上的中线
∴OC⊥AB,且点C在圆上
∴AB是⊙O的切线
O
C
B
A
这种证明切线的方法简记为:“有交点,连半径,证垂直”
注意:使用此方法时必须已知直线与圆有一公共点。
练习1、如图,AB是⊙O的直径,∠ABC=45°,AC=AB,AC是⊙O的切线吗?为什么?
解:∵AB=AC ∴∠ACB=∠ABC=450 ∴∠BAC=900 即AB⊥AC ∵ AB是⊙O的直径 ∴ AC是⊙O的切线
变式练习
练习2、如图:线段AB经过圆心O,交⊙O于点A、C,∠BAD=∠B = 30°,边BD交圆于点D。BD是⊙O的切线吗?为什么?
解:BD是⊙O的切线
连接OD ∵ OD=OA ∴∠ODA=∠BAD=∠B=300 ∴∠ BOD=600 ∴∠ODB=900 即:OD⊥DB 且点O在圆上
∴BD是⊙O的切线
变式练习
证明:连结OP。
∵ AB为直径
∴ OB=OA,BP=PC,
∴OP∥AC。
又∵ PE⊥AC,
∴PE⊥OP,且点P在圆上
∴PE为⊙0的切线。
练习3,△ABC中,以AB为直径的⊙O,交边BC于P, BP=PC, PE⊥AC于E。
求证:PE是⊙O的切线。
变式练习
例2:已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
D
证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。
与例1比较,你发现了什么?
已知如图,△ABC为等腰三角形,O是底边BC的中点,⊙O与腰AB相切于点D。AC与⊙O相切吗?为什么?
E
解:AC与⊙O相切 连接OD,作OE⊥AC ∴∠OEC=900 ∵ AB是⊙O的切线∴OD⊥AB, ∴∠ODB=900=∠OEC ∵AB=AC ∴∠B=∠C ∵O是BC的中点∴OB=OC ∴△OBD≌△OCE ∴OD=OE ∴AC与⊙O相切
无交点,作垂直,证半径
小 结
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:知交点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:无交点,作垂直,证半径。
例3 如图,AB是⊙O的直径, C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D. 求证:AC平分∠DAB.
证明:连接OC.
∵CD 是⊙O的切线,
∴OC⊥CD.
又∵AD⊥CD , ∴OC//AD.
∴∠ACO= ∠CAD .
又∵OC=OA,
∴∠CAO= ∠ACO
∴∠CAD= ∠CAO ,
故AC平分∠DAB.
圆心与切点的连线是常添的辅助线!
1, 如图:AC是⊙O的切线,∠B=600。求∠CAD= 。
C
2,如图:以O为圆心的同心圆,大圆的弦AB是小圆的切线,C是切点,求证:C是AB的中点。
课堂小结
1. 判定切线的方法有哪些?
直线l
与圆有唯一公共点
与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
l是圆的切线
2.常用的添辅助线方法?
⑴直线与圆的公共点已知时,作出过公共点的半径,
再证半径垂直于该直线。(连半径,证垂直)
⑵直线与圆的公共点不确定时,过圆心作直线的垂线
段,再证明这条垂线段等于圆的半径。(作垂直,证半径)
l是圆的切线
l是圆的切线
3.圆的切线性质定理:圆的切线垂直于圆的半径。
辅助线作法:连接圆心与切点可得半径与切线垂直。即“连半径,得垂直”。
1、已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.
求证:DC是⊙O的切线.
证明:连结OD.
∵OA=OD,∴∠1=∠2,
∵AD∥OC,∴∠1=∠3、∠2=∠4
∴∠3=∠4
在△OBC和△ODC中,
OB=OD,∠3=∠4,OC=OC ,
∴△OBC≌△ODC,∴∠OBC=∠ODC
∵BC是⊙O的切线,∴∠OBC=90°,∴∠ODC=90°.
∴DC是⊙O的切线.
2、求证:如果圆的两条切线互相平行,则连结两个切点的线段是直径。
已知:AB、CD是⊙O的两条切线,E、F为切点,且AB∥CD
求证:连结E、F的线段是直径。
证明:连结EO并延长
∵AB切⊙O于E,∴OE⊥AB,
∵AB∥CD,∴OE⊥CD.
∵CD是⊙O切线,F为切点,∴OE必过切点F
∴EF为⊙O直径
3、如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于点E,
求证:CD与小圆相切
证明:连结OE,过O作OF⊥CD,垂足为F
∵AB与小圆O切于点点E,∴OE⊥AB.
又∵AB=CD,
∴OF=OE,又OF⊥CD,
∴CD与小圆O相切.
4、已知:AB是半⊙O直径,CD⊥AB于D,EC是切线,E为切点
求证:CE=CF
证明:连结OE
∵BE=BO∴∠3=∠B
∵CE切⊙O于E
∴OE⊥CE? ∠2+∠3=90°
∵CD⊥AB? ∴∠4+∠B=90°
∴∠2=∠4
∵∠1=∠4? ∴∠1=∠2
∴CE=CF
作业:
1、阅读教材P35-36
2、P36练习第1、2、3题
3、选做基础训练24.4部分习题
相信自己
再见!
