北师大版六年级数学下册课件1.3 圆柱的表面积(28张ppt)
文档属性
| 名称 | 北师大版六年级数学下册课件1.3 圆柱的表面积(28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
第3课时 圆柱的表面积
1.通过动手操作,探索圆柱侧面积的计算方法,
掌握圆柱侧面积和表面积的计算方法。(重点)
2.理解圆柱的侧面展开图与圆柱的关系。(难点)
(1)我们学过计算哪些图形的表面积?它们的表面积怎
样计算?
答:S长=长×宽 S正=边长×边长 S圆=πr2
知识点
圆柱侧面积的计算方法
想一想,怎样计算圆柱的体积呢?
圆柱的侧面展开后是一个怎样的图形呢?你能想办法说明吗?
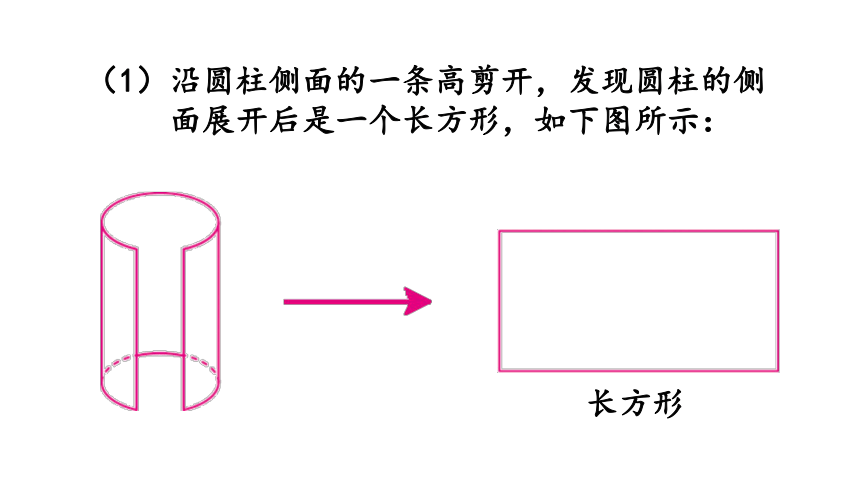
(1)沿圆柱侧面的一条高剪开,发现圆柱的侧
面展开后是一个长方形,如下图所示:
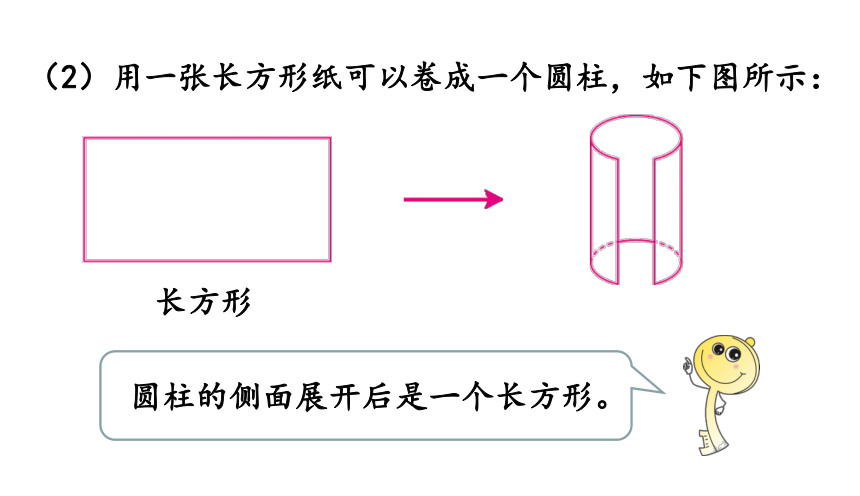
(2)用一张长方形纸可以卷成一个圆柱,如下图所示:
圆柱的侧面沿高展开后得到的长方形的长就是圆柱的底面周长,宽就是圆柱的高。
长方形的长=圆柱的底面周长,
长方形的宽=圆柱的高,所以可以得到:
长方形的面积 = 长 × 宽
圆柱的侧面积 = 底面周长×高
如果用S侧表示圆柱的侧面积,用C表示底面周长,用h表示高,用d表示底面圆的直径,r表示底面圆的半径,那么圆柱的侧面积的计算公式是:
S侧=Ch、S侧=πdh 或S侧=2πrh。
知识提炼
1、圆柱的侧面沿高展开后是一个长方形。
2、圆柱的侧面积=底面周长×高,用字
母表示为:
S侧=Ch、S侧=πdh 或S侧=2πrh。
(1)把圆柱的侧面沿着一条高展开,可以得到一
个( ),它的长等于圆柱的( ),
宽等于圆柱的( )
小试牛刀
长方形
(2)一个圆柱的侧面积是12.56 cm2,底面积是
3.14 cm2,它的表面积是( )cm2。
填空题
底面周长
高
18.84
侧面积:2×3.14×10×30=1884(cm2)
底面积:3.14×102=314(cm2)
表面积:1884+314×2=2512(cm2)
答:至少需要用2512 cm2 的纸板。
知识点
圆柱侧面积的计算方法
如图所示,要做一个圆柱形纸盒。如果接口不计,至少需要用多大面积的纸板?
知识提炼
圆柱的表面积=圆柱的侧面积+底面积×2,
用字母表示为S表=S侧+2S底。
小试牛刀
王阿姨做了一个圆柱形的抱枕,长80 cm,底面直径为18 cm。如果侧面用花布,底面用黄布,两种布各需要多少?
花布:18×3.14×80=4521.6(cm2)
黄布:(18÷2)2×3.14×2=508.68(cm2)
答:花布需要4521.6 cm2;黄布需要508.68 cm2;
例 判断:圆柱的侧面展开图一定是长方形或正方
形。 ( )
错误解答:√
正确解答:×
1.连一连,并在括号中填出相应的数。
(选自教材P6 T1)
9.42cm
8cm
21.98cm
4cm
2.求圆柱的表面积。
(选自教材P6 T2)
3.14×(4÷2)2×2+6×4×3.14
=3.14×4×2+24×3.14
=100.48(cm2)
3.14×32×2+10×2×3.14×3
=18×3.14+60×3.14
=244.92(dm2)
侧面积=底面周长×高
3.制作一个底面直径20 cm,长50 cm的圆柱形通风
管,至少要用多少平方厘米铁皮?
3.14×20×50=3140(cm2)
答:至少要用3140平方厘米铁皮。
(选自教材P6 T3)
4.压路机前轮直径是1.6m,宽是2m,它转动一周,
压路的面积是多少平方米?
3.14×1.6×2=10.048(m2)
答:压路的面积是10.048平方米。
(选自教材P6 T4)
5.一个圆柱形水池,水池内壁和底部都镶上瓷砖,
水池内部底面周长25.12 m,池深1.2 m,镶瓷砖
的面积是多少平方米?
侧面积:25.12×1.2=30.144(m2)
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
表面积:30.144+50.24=80.384(m2)
答:镶瓷砖的面积是80.384平方米。
1、圆柱的侧面沿高展开后是一个长方形。
2、圆柱的侧面积=底面周长×高,用字
母表示为:
S侧=Ch、S侧=πdh 或S侧=2πrh。
3.圆柱的表面积=圆柱的侧面积+底面积×2,
用字母表示为S表=S侧+2S底。
作业:完成教材相关练习题。
第3课时 圆柱的表面积
1.通过动手操作,探索圆柱侧面积的计算方法,
掌握圆柱侧面积和表面积的计算方法。(重点)
2.理解圆柱的侧面展开图与圆柱的关系。(难点)
(1)我们学过计算哪些图形的表面积?它们的表面积怎
样计算?
答:S长=长×宽 S正=边长×边长 S圆=πr2
知识点
圆柱侧面积的计算方法
想一想,怎样计算圆柱的体积呢?
圆柱的侧面展开后是一个怎样的图形呢?你能想办法说明吗?
(1)沿圆柱侧面的一条高剪开,发现圆柱的侧
面展开后是一个长方形,如下图所示:
(2)用一张长方形纸可以卷成一个圆柱,如下图所示:
圆柱的侧面沿高展开后得到的长方形的长就是圆柱的底面周长,宽就是圆柱的高。
长方形的长=圆柱的底面周长,
长方形的宽=圆柱的高,所以可以得到:
长方形的面积 = 长 × 宽
圆柱的侧面积 = 底面周长×高
如果用S侧表示圆柱的侧面积,用C表示底面周长,用h表示高,用d表示底面圆的直径,r表示底面圆的半径,那么圆柱的侧面积的计算公式是:
S侧=Ch、S侧=πdh 或S侧=2πrh。
知识提炼
1、圆柱的侧面沿高展开后是一个长方形。
2、圆柱的侧面积=底面周长×高,用字
母表示为:
S侧=Ch、S侧=πdh 或S侧=2πrh。
(1)把圆柱的侧面沿着一条高展开,可以得到一
个( ),它的长等于圆柱的( ),
宽等于圆柱的( )
小试牛刀
长方形
(2)一个圆柱的侧面积是12.56 cm2,底面积是
3.14 cm2,它的表面积是( )cm2。
填空题
底面周长
高
18.84
侧面积:2×3.14×10×30=1884(cm2)
底面积:3.14×102=314(cm2)
表面积:1884+314×2=2512(cm2)
答:至少需要用2512 cm2 的纸板。
知识点
圆柱侧面积的计算方法
如图所示,要做一个圆柱形纸盒。如果接口不计,至少需要用多大面积的纸板?
知识提炼
圆柱的表面积=圆柱的侧面积+底面积×2,
用字母表示为S表=S侧+2S底。
小试牛刀
王阿姨做了一个圆柱形的抱枕,长80 cm,底面直径为18 cm。如果侧面用花布,底面用黄布,两种布各需要多少?
花布:18×3.14×80=4521.6(cm2)
黄布:(18÷2)2×3.14×2=508.68(cm2)
答:花布需要4521.6 cm2;黄布需要508.68 cm2;
例 判断:圆柱的侧面展开图一定是长方形或正方
形。 ( )
错误解答:√
正确解答:×
1.连一连,并在括号中填出相应的数。
(选自教材P6 T1)
9.42cm
8cm
21.98cm
4cm
2.求圆柱的表面积。
(选自教材P6 T2)
3.14×(4÷2)2×2+6×4×3.14
=3.14×4×2+24×3.14
=100.48(cm2)
3.14×32×2+10×2×3.14×3
=18×3.14+60×3.14
=244.92(dm2)
侧面积=底面周长×高
3.制作一个底面直径20 cm,长50 cm的圆柱形通风
管,至少要用多少平方厘米铁皮?
3.14×20×50=3140(cm2)
答:至少要用3140平方厘米铁皮。
(选自教材P6 T3)
4.压路机前轮直径是1.6m,宽是2m,它转动一周,
压路的面积是多少平方米?
3.14×1.6×2=10.048(m2)
答:压路的面积是10.048平方米。
(选自教材P6 T4)
5.一个圆柱形水池,水池内壁和底部都镶上瓷砖,
水池内部底面周长25.12 m,池深1.2 m,镶瓷砖
的面积是多少平方米?
侧面积:25.12×1.2=30.144(m2)
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
表面积:30.144+50.24=80.384(m2)
答:镶瓷砖的面积是80.384平方米。
1、圆柱的侧面沿高展开后是一个长方形。
2、圆柱的侧面积=底面周长×高,用字
母表示为:
S侧=Ch、S侧=πdh 或S侧=2πrh。
3.圆柱的表面积=圆柱的侧面积+底面积×2,
用字母表示为S表=S侧+2S底。
作业:完成教材相关练习题。
