2020年高考数学专题练习:新型冠状病毒(PDF版含答案)
文档属性
| 名称 | 2020年高考数学专题练习:新型冠状病毒(PDF版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 917.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 08:31:45 | ||
图片预览


文档简介
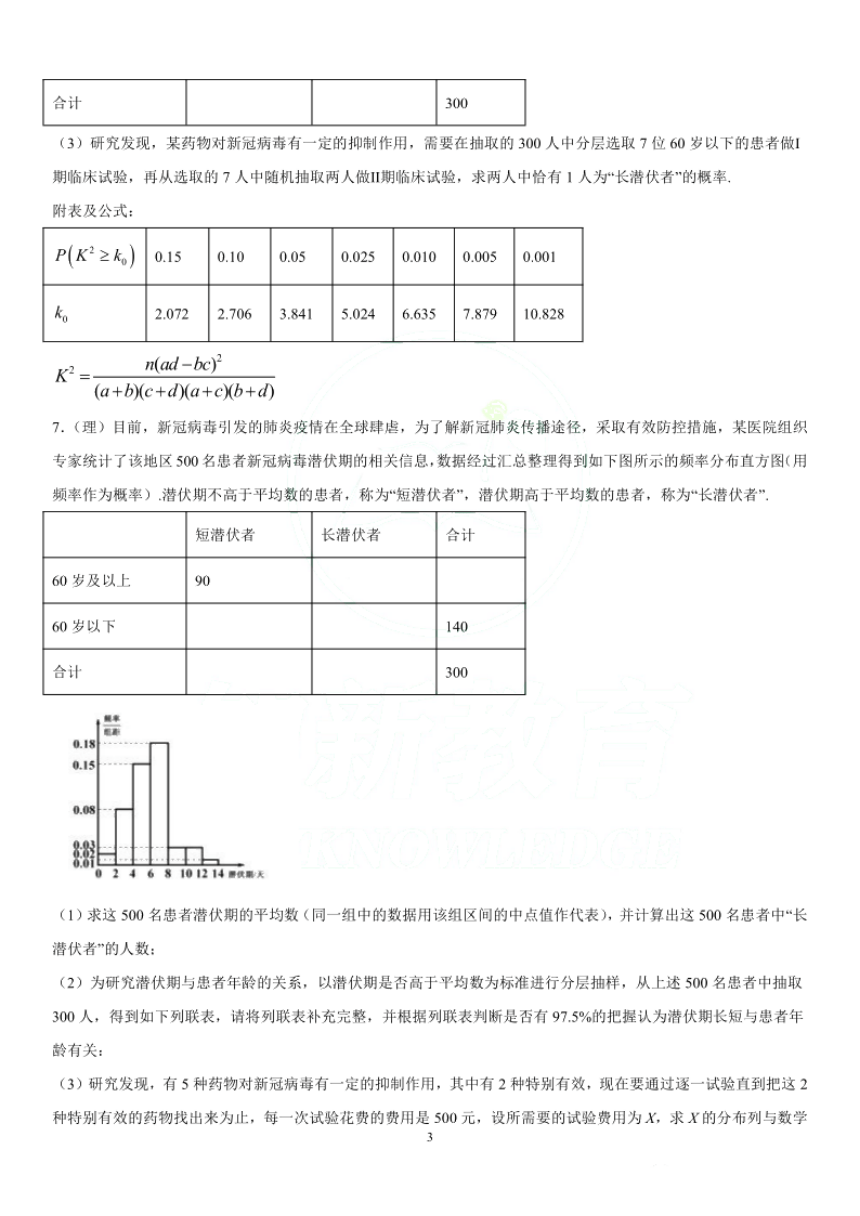
2020年高考
有关新型冠状病毒的数学题预测
1.(理)己知箱中装有6瓶消毒液,其中4瓶合格品,2瓶不合格品,现从箱中毎次取一瓶消毒液,毎瓶消毒液被
抽到的可能性相同,不放回地抽取两次,若用A表示“第一次取到不合格消毒液”,用B表示“第二次仍取到不合格
消毒液”,则P(B|A)=()
B
C
6
4
2.2020年初,新型冠状病毒(COVD-19)引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗
方法,取得了不错的成效,某地开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
周数(x)
2
3
4
治愈人数(y)|2
17
36
93
142
由表格可得y关于x的二次回归方程为j=6x2+a,则此回归模型第4周的残差(实际值与预报值之差)为()
B.4
C.1
3.2020年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒薆延,各级政府相继启动重大突发公共卫生事件
一级响应,全国人心抗击疫情.下图表示1月21日至3月7日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,
则下列中表述错误的是()
15000人数
12000
9000
6000
3000
新增治愈
小节小。乎式小日期
A.2月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数
C.2月10日至2月14日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在2月12日左右达到峰值
4.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,
有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各
个选项中,一定符合上述指标的是
①平均数x≤3:②标准差S≤2:③平均数x≤3且标准差S≤2:
④平均数x≤3且极差小于或等于2
⑤众数等于1且极差小于或等于4.
5.疫情期间,某小区超市平面图如图所示,由矩形OABC与扇形OCD组成,OA=30米,AB=50米,∠COD令
经营者决定在O点处安装一个监控摄像头,摄像头的监控视角∠EOF≡一,摄像头监控区域为图中阴影部分,要
求点E在弧CD上,点F在线段AB上设∠FOC=O
(1)求该监控摄像头所能监控到的区域面积S关于O的函数关系式,并求出tanO的取值范围
(2)求监控区域面积S最大时,角θ的正切值
6.目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医阬组织专家
统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频
率作为概率)潜伏期不高于平均数的患者,称为短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”
0.18
0.08
02468101214伏天
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长
潜伏者”的人数
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取
300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年
龄有关;
短潜伏者
长潜伏者
合计
60岁及以上
90
60岁以下
140
有关新型冠状病毒的数学题预测
1.(理)己知箱中装有6瓶消毒液,其中4瓶合格品,2瓶不合格品,现从箱中毎次取一瓶消毒液,毎瓶消毒液被
抽到的可能性相同,不放回地抽取两次,若用A表示“第一次取到不合格消毒液”,用B表示“第二次仍取到不合格
消毒液”,则P(B|A)=()
B
C
6
4
2.2020年初,新型冠状病毒(COVD-19)引起的肺炎疫情爆发以来,各地医疗机构采取了各种针对性的治疗
方法,取得了不错的成效,某地开始使用中西医结合方法后,每周治愈的患者人数如下表所示:
周数(x)
2
3
4
治愈人数(y)|2
17
36
93
142
由表格可得y关于x的二次回归方程为j=6x2+a,则此回归模型第4周的残差(实际值与预报值之差)为()
B.4
C.1
3.2020年初,湖北出现由新型冠状病毒引发的肺炎.为防止病毒薆延,各级政府相继启动重大突发公共卫生事件
一级响应,全国人心抗击疫情.下图表示1月21日至3月7日我国新型冠状病毒肺炎单日新增治愈和新增确诊病例数,
则下列中表述错误的是()
15000人数
12000
9000
6000
3000
新增治愈
小节小。乎式小日期
A.2月下旬新增确诊人数呈波动下降趋势
B.随着全国医疗救治力度逐渐加大,2月下旬单日治愈人数超过确诊人数
C.2月10日至2月14日新增确诊人数波动最大
D.我国新型冠状病毒肺炎累计确诊人数在2月12日左右达到峰值
4.在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,
有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各
个选项中,一定符合上述指标的是
①平均数x≤3:②标准差S≤2:③平均数x≤3且标准差S≤2:
④平均数x≤3且极差小于或等于2
⑤众数等于1且极差小于或等于4.
5.疫情期间,某小区超市平面图如图所示,由矩形OABC与扇形OCD组成,OA=30米,AB=50米,∠COD令
经营者决定在O点处安装一个监控摄像头,摄像头的监控视角∠EOF≡一,摄像头监控区域为图中阴影部分,要
求点E在弧CD上,点F在线段AB上设∠FOC=O
(1)求该监控摄像头所能监控到的区域面积S关于O的函数关系式,并求出tanO的取值范围
(2)求监控区域面积S最大时,角θ的正切值
6.目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医阬组织专家
统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频
率作为概率)潜伏期不高于平均数的患者,称为短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”
0.18
0.08
02468101214伏天
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长
潜伏者”的人数
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取
300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年
龄有关;
短潜伏者
长潜伏者
合计
60岁及以上
90
60岁以下
140
同课章节目录
