2020年春山东省人教版七年级数学下册《9.3一元一次不等式组》课件(1)(26张PPT)
文档属性
| 名称 | 2020年春山东省人教版七年级数学下册《9.3一元一次不等式组》课件(1)(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
2020年春山东新课标人教版七年级数学下册
《9.3一元一次不等式组》(1)
学习目标
1.理解一元一次不等式组和一
元一次不等式组解集的概念;
2.会解由两个一元一次不等式
组成的不等式组.
一、问题解决 温故孕新
1.解下列不等式,并在数轴上表示解集.
一、问题解决 温故孕新
1.解下列不等式,并在数轴上表示解集.
一、问题解决 温故孕新
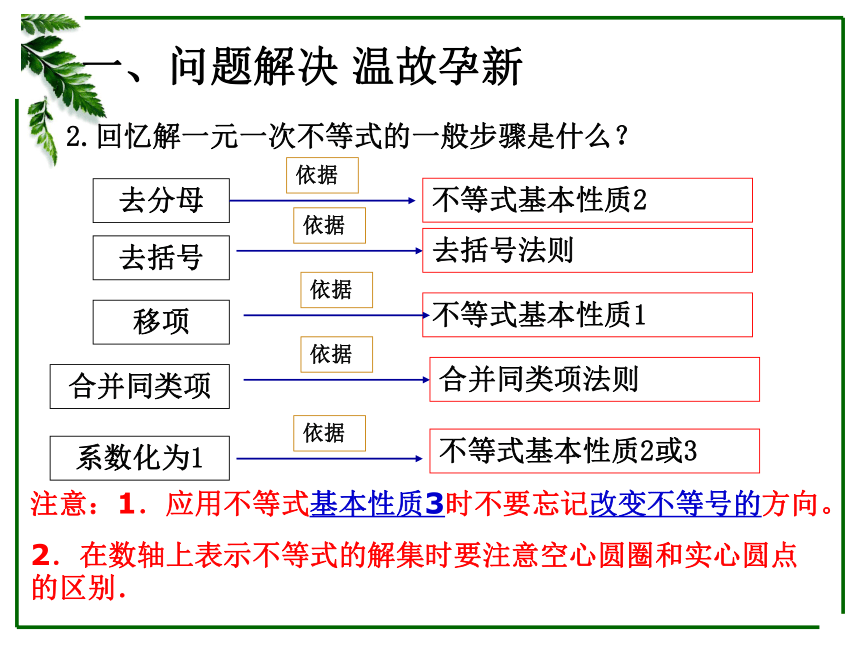
2.回忆解一元一次不等式的一般步骤是什么?
去分母
去括号
移项
合并同类项
系数化为1
不等式基本性质2
去括号法则
不等式基本性质1
合并同类项法则
不等式基本性质2或3
注意:1.应用不等式基本性质3时不要忘记改变不等号的方向。
2.在数轴上表示不等式的解集时要注意空心圆圈和实心圆点的区别.
二、问题研究 借故生新
注意:
(1)每个不等式必须为一元一次不等式.
(2)不等式必须是只含有同一个未知数.
(3)不等式的数量至少是两个或者多个.
1.一元一次不等式组:
类似于方程组,把这两个或两个以上的一元一次
不等式合起来,就组成一个一元一次不等式组.
记作
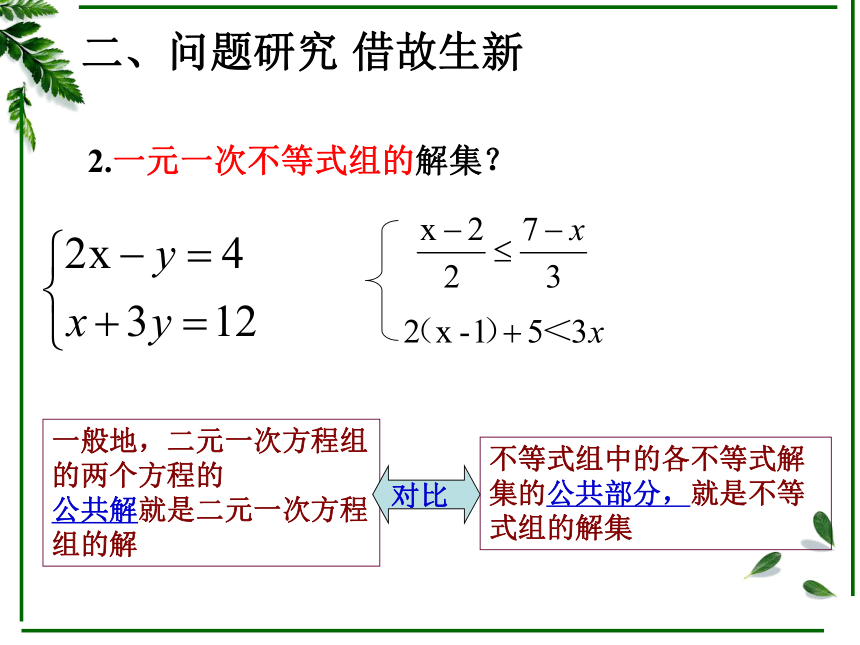
2.一元一次不等式组的解集?
不等式组中的各不等式解集的公共部分,就是不等式组的解集
一般地,二元一次方程组的两个方程的
公共解就是二元一次方程组的解
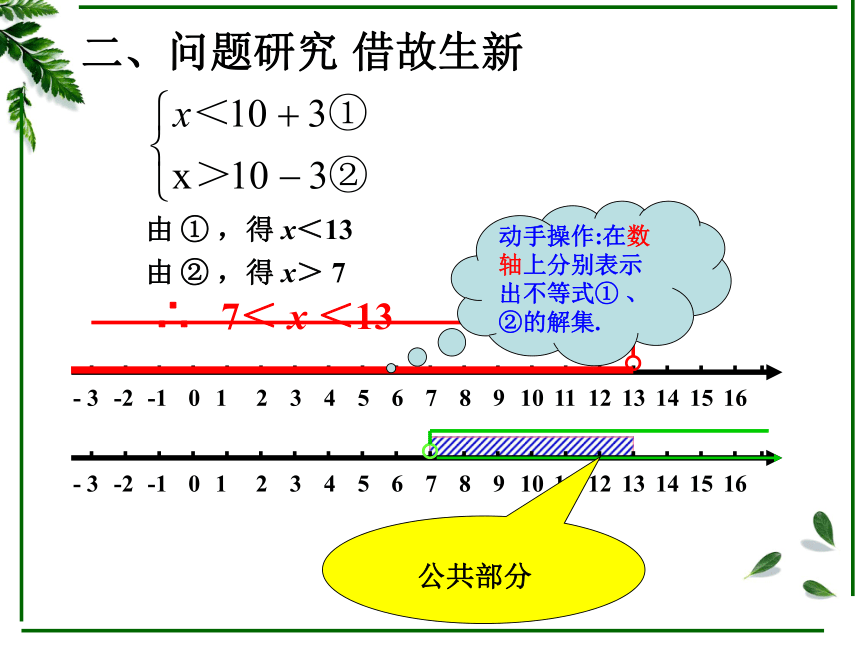
由 ① ,得 x<13
由 ② ,得 x> 7
∴ 7< x <13
公共部分
动手操作:在数轴上分别表示出不等式① 、②的解集.
1.两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组.
2.两个不等式的解集的公共部分叫做由它们所组成的不等式组的解集.
3.解不等式组就是求它的解集.
总结:
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分.
2
0
1
例1.利用数轴判断下列不等式组是否有解集?如有,请写出.
不等式组的解集为x<1
都小取较小
不等式组的解集为x>3
都大取较大
例1.利用数轴判断下列不等式组
是否有解集?如有,请写出.
不等式组的解集为1<x< 3
大小小大中间找
例1.利用数轴判断下列不等式组是否有解集? 如有,请写出。
不等式组的解集为空集,即:不等式组无解
大大小小无解了
例1.利用数轴判断下列不等式组
是否有解集?如有,请写出。
都小取较小
2.都大取较大
3. 大小小大中间找
4.大大小小无解了
运用规律求下列不等式组的解集,比一比看谁最快.
1. 都大取较大
2.都小取较小
3. 大小小大中间找
4.大大小小无解了
x>2
x>-2
x<3
x<-4
3 -1 无解
设a<b,你能说出下列四种情况下不等式组的解集吗?用数轴试一试
x>b
x<a
无解
a<x<b
大小小大中间找
大大小小无解了
两小取小
两大取大
规律(口诀)
设a < b 在数轴上表示解集 不等式组的解集
解不等式①得:x>2
解不等式②得:x≥3
在数轴上表示不等式①、②的解集:
解:
因此,原不等式组无解 。
解:解不等式①,得
解不等式②,得
A. 解下列不等式组
(1)x>1
(2)无解
(3)-2.4<x<3.5
D
C
A. x≥2 B. x≤2 C. 无解 D. x=2
A. 0 ,1 B. 0 C. 1 D. x≤1
(4)不等式组 的解集在数轴上表示为
( )
C
B
(3)不等式组 的负整数解是 ( )
A. -2, 0, -1 B. -2, C. -2,-1 D.不能确定
四、课堂小结 返故悟新
1.本节课你掌握了哪些数学知识?
2.本节课你学会了哪些解题方法?
3.本节课你运用了哪些数学思想?
4.本节课你出现了哪些问题?
四、课堂小结 返故悟新
1.一元一次不等式组的定义
2.一元一次不等式组的解集和解不等式组
3.如何利用数轴找出一元一次不等式组的解集:
四、课堂小结 返故悟新
解一元一次不等式组的步骤
解:【在原不等式组上分别标上①②】
(1)解①得:
(2)解②得:
(3)把不等式①和②的解集在数轴上表示出来
(4)写出不等式组的解集
五、作业布置 运故用新
课本第130页习题9.3
2.解下列不等式组
2020年春山东新课标人教版七年级数学下册
《9.3一元一次不等式组》(1)
学习目标
1.理解一元一次不等式组和一
元一次不等式组解集的概念;
2.会解由两个一元一次不等式
组成的不等式组.
一、问题解决 温故孕新
1.解下列不等式,并在数轴上表示解集.
一、问题解决 温故孕新
1.解下列不等式,并在数轴上表示解集.
一、问题解决 温故孕新
2.回忆解一元一次不等式的一般步骤是什么?
去分母
去括号
移项
合并同类项
系数化为1
不等式基本性质2
去括号法则
不等式基本性质1
合并同类项法则
不等式基本性质2或3
注意:1.应用不等式基本性质3时不要忘记改变不等号的方向。
2.在数轴上表示不等式的解集时要注意空心圆圈和实心圆点的区别.
二、问题研究 借故生新
注意:
(1)每个不等式必须为一元一次不等式.
(2)不等式必须是只含有同一个未知数.
(3)不等式的数量至少是两个或者多个.
1.一元一次不等式组:
类似于方程组,把这两个或两个以上的一元一次
不等式合起来,就组成一个一元一次不等式组.
记作
2.一元一次不等式组的解集?
不等式组中的各不等式解集的公共部分,就是不等式组的解集
一般地,二元一次方程组的两个方程的
公共解就是二元一次方程组的解
由 ① ,得 x<13
由 ② ,得 x> 7
∴ 7< x <13
公共部分
动手操作:在数轴上分别表示出不等式① 、②的解集.
1.两个或两个以上的一元一次不等式合起来,就组成一个一元一次不等式组.
2.两个不等式的解集的公共部分叫做由它们所组成的不等式组的解集.
3.解不等式组就是求它的解集.
总结:
把下列不等式组中两个不等式的解集分别在同一数轴上表示出来,并观察其公共部分.
2
0
1
例1.利用数轴判断下列不等式组是否有解集?如有,请写出.
不等式组的解集为x<1
都小取较小
不等式组的解集为x>3
都大取较大
例1.利用数轴判断下列不等式组
是否有解集?如有,请写出.
不等式组的解集为1<x< 3
大小小大中间找
例1.利用数轴判断下列不等式组是否有解集? 如有,请写出。
不等式组的解集为空集,即:不等式组无解
大大小小无解了
例1.利用数轴判断下列不等式组
是否有解集?如有,请写出。
都小取较小
2.都大取较大
3. 大小小大中间找
4.大大小小无解了
运用规律求下列不等式组的解集,比一比看谁最快.
1. 都大取较大
2.都小取较小
3. 大小小大中间找
4.大大小小无解了
x>2
x>-2
x<3
x<-4
3
设a<b,你能说出下列四种情况下不等式组的解集吗?用数轴试一试
x>b
x<a
无解
a<x<b
大小小大中间找
大大小小无解了
两小取小
两大取大
规律(口诀)
设a < b 在数轴上表示解集 不等式组的解集
解不等式①得:x>2
解不等式②得:x≥3
在数轴上表示不等式①、②的解集:
解:
因此,原不等式组无解 。
解:解不等式①,得
解不等式②,得
A. 解下列不等式组
(1)x>1
(2)无解
(3)-2.4<x<3.5
D
C
A. x≥2 B. x≤2 C. 无解 D. x=2
A. 0 ,1 B. 0 C. 1 D. x≤1
(4)不等式组 的解集在数轴上表示为
( )
C
B
(3)不等式组 的负整数解是 ( )
A. -2, 0, -1 B. -2, C. -2,-1 D.不能确定
四、课堂小结 返故悟新
1.本节课你掌握了哪些数学知识?
2.本节课你学会了哪些解题方法?
3.本节课你运用了哪些数学思想?
4.本节课你出现了哪些问题?
四、课堂小结 返故悟新
1.一元一次不等式组的定义
2.一元一次不等式组的解集和解不等式组
3.如何利用数轴找出一元一次不等式组的解集:
四、课堂小结 返故悟新
解一元一次不等式组的步骤
解:【在原不等式组上分别标上①②】
(1)解①得:
(2)解②得:
(3)把不等式①和②的解集在数轴上表示出来
(4)写出不等式组的解集
五、作业布置 运故用新
课本第130页习题9.3
2.解下列不等式组
