高中数学人教B版选修1-1 利用导数研究函数极值(1) 课件(30张ppt)
文档属性
| 名称 | 高中数学人教B版选修1-1 利用导数研究函数极值(1) 课件(30张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
利用导数研究函数极值(1)
高二年级 数学
问题1 观察下列函数图象(图1-图3),请说出图中的点A,B,C,D,E有什么共同的特点?
局部最值
导数值等于0
(一)创设问题情境
图1
图2
图3
极大值
极小值
问题1 观察下列函数图象(图1-图3),请说出图中的点A,B,C,D,E有什么共同的特点?
(一)创设问题情境
图1
图2
图3
函数值1,是正弦函数的极大值;
函数值-1,是正弦函数的极小值.
问题2 还能再列举出一个有上述类似特征的函数吗?
图4
(二)举例感知
问题3 根据前面的分析,你能试着给出函数极大值与极小值的定义吗?
(三)形成概念
问题3 根据前面的分析,你能试着给出函数极大值与极小值的定义吗?
(三)形成概念
极大值与极小值统称为极值.
极大值点与极小值点统称为极值点.
极值与极值点
(1)存在一个包含x0的开区间;
(2)横坐标x0称为函数f(x)的一个极值点,极值点不是一个点.
(四)概念辨析
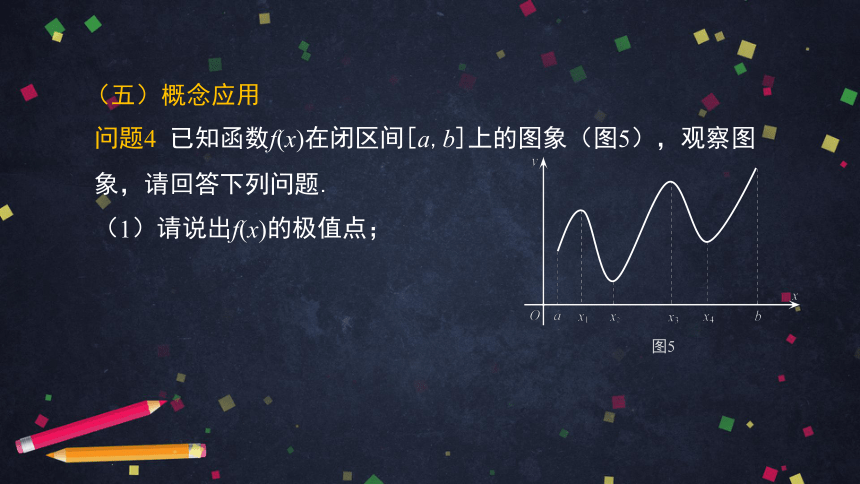
问题4 已知函数f(x)在闭区间[a,b]上的图象(图5),观察图象,请回答下列问题.
(1)请说出f(x)的极值点;
(五)概念应用
图5
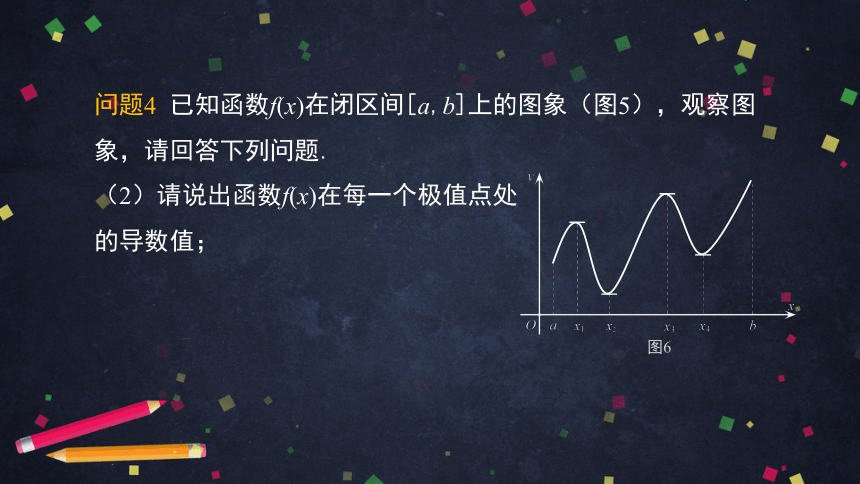
问题4 已知函数f(x)在闭区间[a,b]上的图象(图5),观察图象,请回答下列问题.
(2)请说出函数f(x)在每一个极值点处
的导数值;
图6
问题4 已知函数f(x)在闭区间[a,b]上的图象(图5),观察图象,请回答下列问题.
(3)请说出在极大值点与极小值点附
近函数及其导数的取值情况.
图6
(六)例题解析
图7
图8
图9
图10
图10
图11
图12
图12
图12
1.发现并得到函数极值概念;
课堂小结
2.理解并掌握函数极值概念;
3.归纳并得到求函数极值的步骤;
4.解决函数极值的具体问题.
课后作业
求函数 的极值.
利用导数研究函数极值(1)
高二年级 数学
问题1 观察下列函数图象(图1-图3),请说出图中的点A,B,C,D,E有什么共同的特点?
局部最值
导数值等于0
(一)创设问题情境
图1
图2
图3
极大值
极小值
问题1 观察下列函数图象(图1-图3),请说出图中的点A,B,C,D,E有什么共同的特点?
(一)创设问题情境
图1
图2
图3
函数值1,是正弦函数的极大值;
函数值-1,是正弦函数的极小值.
问题2 还能再列举出一个有上述类似特征的函数吗?
图4
(二)举例感知
问题3 根据前面的分析,你能试着给出函数极大值与极小值的定义吗?
(三)形成概念
问题3 根据前面的分析,你能试着给出函数极大值与极小值的定义吗?
(三)形成概念
极大值与极小值统称为极值.
极大值点与极小值点统称为极值点.
极值与极值点
(1)存在一个包含x0的开区间;
(2)横坐标x0称为函数f(x)的一个极值点,极值点不是一个点.
(四)概念辨析
问题4 已知函数f(x)在闭区间[a,b]上的图象(图5),观察图象,请回答下列问题.
(1)请说出f(x)的极值点;
(五)概念应用
图5
问题4 已知函数f(x)在闭区间[a,b]上的图象(图5),观察图象,请回答下列问题.
(2)请说出函数f(x)在每一个极值点处
的导数值;
图6
问题4 已知函数f(x)在闭区间[a,b]上的图象(图5),观察图象,请回答下列问题.
(3)请说出在极大值点与极小值点附
近函数及其导数的取值情况.
图6
(六)例题解析
图7
图8
图9
图10
图10
图11
图12
图12
图12
1.发现并得到函数极值概念;
课堂小结
2.理解并掌握函数极值概念;
3.归纳并得到求函数极值的步骤;
4.解决函数极值的具体问题.
课后作业
求函数 的极值.
