人教版八年级下册数学 18.1.1 平行四边形及其性质(一) 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级下册数学 18.1.1 平行四边形及其性质(一) 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 14:39:36 | ||
图片预览



文档简介
(共22张PPT)
平行四边形及其性质(一)
学习目标
1.理解平行四边形的概念。
2.掌握平行四边形的性质。
3.能够运用平行四边形的性质进行有关的证明和计算。
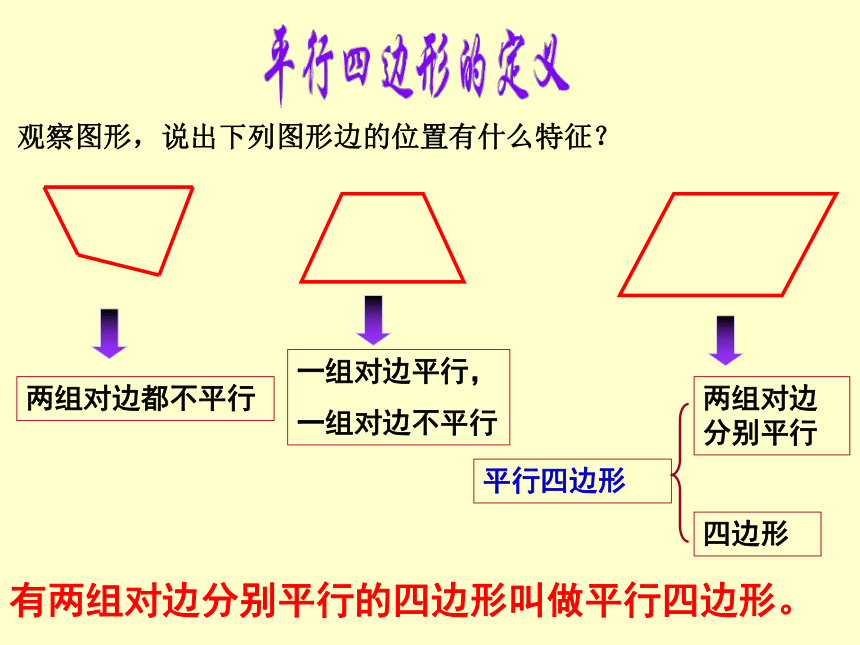
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
有两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
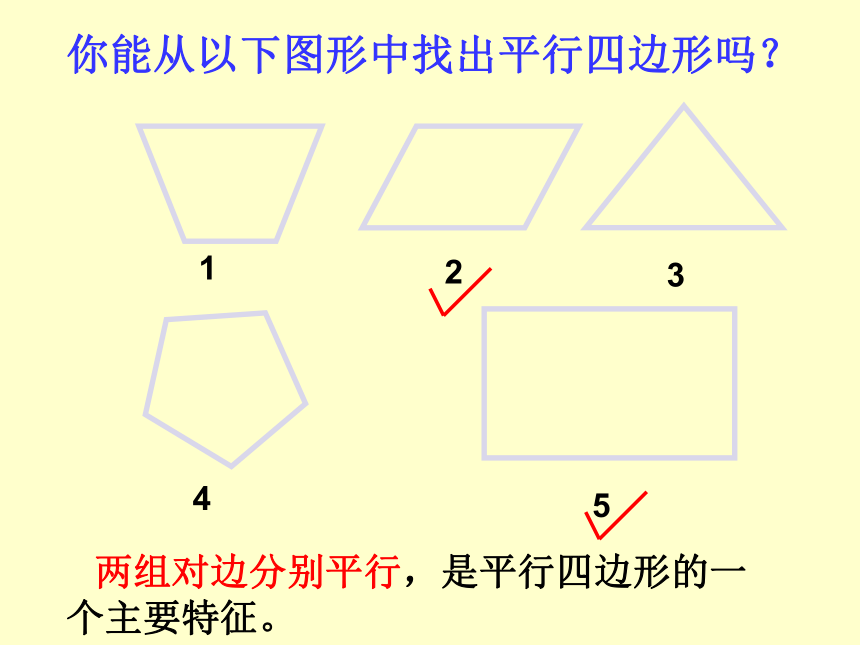
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
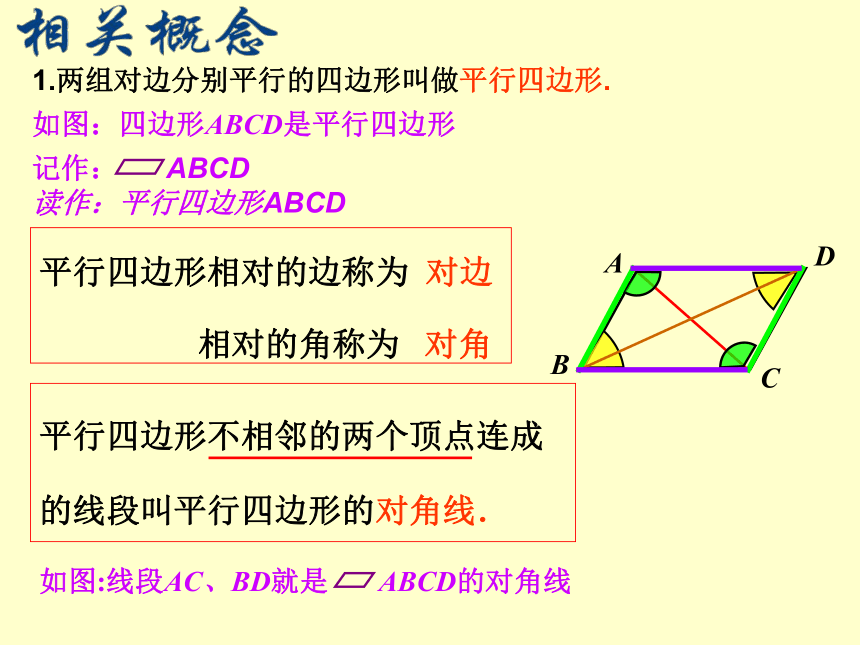
平行四边形相对的边称为 对边
相对的角称为 对角
1.两组对边分别平行的四边形叫做平行四边形.
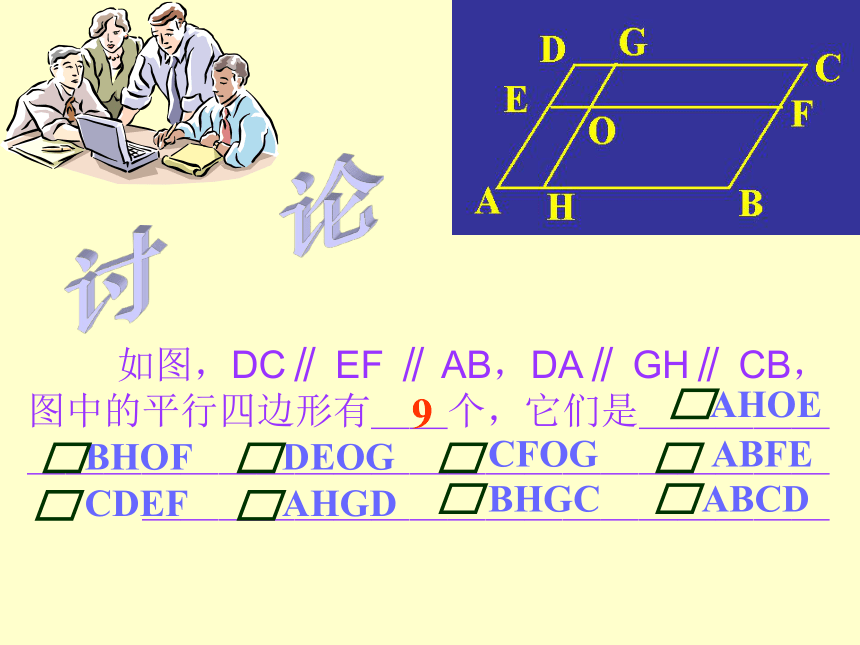
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是____________________________________________
9
A
B
D
C
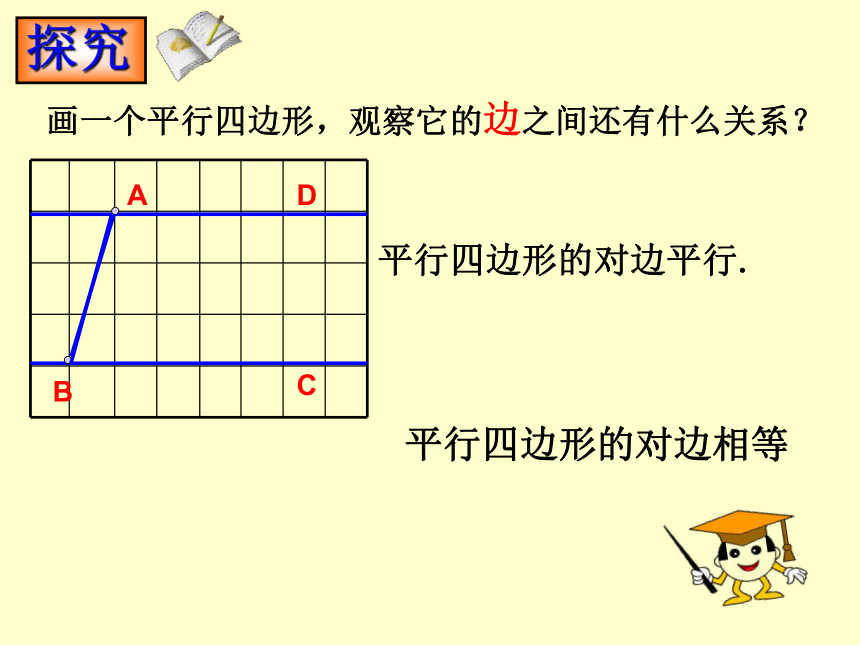
画一个平行四边形,观察它的边之间还有什么关系?
平行四边形的对边平行.
平行四边形的对边相等
探究
探究
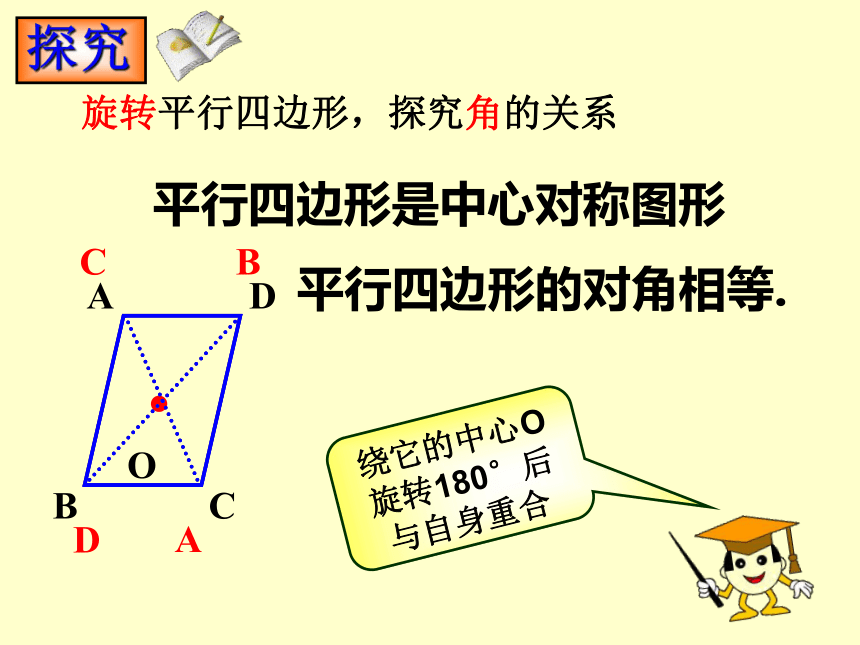
旋转平行四边形,探究角的关系
平行四边形的对角相等.
平行四边形是中心对称图形
绕它的中心O旋转180°后与自身重合
平行四边形的对边相等,对角相等。
验证
已知:四边形ABCD是平行四边形。
求证:AC=BD,AB=CD
∠A= ∠D, ∠B= ∠D.
提示:可连接BC,试证⊿______≌ ⊿______
转化思想:
四边形
问题
三角形
问题
转化
性质2:平行四边形的对角相等。
性质1:平行四边形的对边平行
且相等。
邻角互补。
平行四边形是中心对称图形
解:
例题
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
变式练习:
例题2
解: ∵BD ⊥AD
∴ ∠ADB=90 °
在Rt △ADB中,AD=3,BD=4
∴AB= = 5(勾股定理)
又∵四边形ABCD为平行四边形(已知)
∴ AD=BC=3
AB=DC=5
∴ ABCD的周长=2(AD+AB)
=2(3+5)
=16
(平行四边形对边相等)
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
在 ABCD 中, 已知一个内角的度数是60°,则其余三个内角的度数分别为:
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
可要细心哟
在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=
C
A
B
D
E
9cm
1
2
5cm
9cm
3
平行四边形的对边___。
平行四边形的___,___。
有两组对边 ___的四边形是平行四边形。
平行四边形是__对称图形
4、 ABCD的周长为40cm,⊿ABC的周长为25cm,
则对角 线AC长为( )
A、5cm B、15cm C、6cm D、 16cm
2、在 ABCD 中,∠ADC=120°, ∠CAD=20°,则
∠ABC= , ∠CAB= .
(1小题)
(2小题)
平行四边形及其性质(一)
学习目标
1.理解平行四边形的概念。
2.掌握平行四边形的性质。
3.能够运用平行四边形的性质进行有关的证明和计算。
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
有两组对边分别平行的四边形叫做平行四边形。
观察图形,说出下列图形边的位置有什么特征?
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
平行四边形相对的边称为 对边
相对的角称为 对角
1.两组对边分别平行的四边形叫做平行四边形.
如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是____________________________________________
9
A
B
D
C
画一个平行四边形,观察它的边之间还有什么关系?
平行四边形的对边平行.
平行四边形的对边相等
探究
探究
旋转平行四边形,探究角的关系
平行四边形的对角相等.
平行四边形是中心对称图形
绕它的中心O旋转180°后与自身重合
平行四边形的对边相等,对角相等。
验证
已知:四边形ABCD是平行四边形。
求证:AC=BD,AB=CD
∠A= ∠D, ∠B= ∠D.
提示:可连接BC,试证⊿______≌ ⊿______
转化思想:
四边形
问题
三角形
问题
转化
性质2:平行四边形的对角相等。
性质1:平行四边形的对边平行
且相等。
邻角互补。
平行四边形是中心对称图形
解:
例题
如图: 在 ABCD中,∠A+∠C=200°
则:∠A= ,∠B= .
变式练习:
例题2
解: ∵BD ⊥AD
∴ ∠ADB=90 °
在Rt △ADB中,AD=3,BD=4
∴AB= = 5(勾股定理)
又∵四边形ABCD为平行四边形(已知)
∴ AD=BC=3
AB=DC=5
∴ ABCD的周长=2(AD+AB)
=2(3+5)
=16
(平行四边形对边相等)
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
在 ABCD 中, 已知一个内角的度数是60°,则其余三个内角的度数分别为:
如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
可要细心哟
在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。
在平行四边形ABCD中,若AE平分∠DAB,AB=5cm,AD=9cm,则EC=
C
A
B
D
E
9cm
1
2
5cm
9cm
3
平行四边形的对边___。
平行四边形的___,___。
有两组对边 ___的四边形是平行四边形。
平行四边形是__对称图形
4、 ABCD的周长为40cm,⊿ABC的周长为25cm,
则对角 线AC长为( )
A、5cm B、15cm C、6cm D、 16cm
2、在 ABCD 中,∠ADC=120°, ∠CAD=20°,则
∠ABC= , ∠CAB= .
(1小题)
(2小题)
