冀教版八年级下册数学21.1 一次函数(第一课时 共23张PPT)
文档属性
| 名称 | 冀教版八年级下册数学21.1 一次函数(第一课时 共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
问题
2011年开始运营的京沪高速铁路全长1318千米
设列车的平均速度为300千米每小时。考虑以下问题:
(1)乘高铁,从始发站北京南站到终点站上海站,约需多少小时?(保留一位小数)
(2)京沪高铁的行程ykm与时间th之间有何数量关系?
(3)从北京南站出发2.5小时后是否已过了距始发站1100千米的南京南站?
(1)乘京沪高速列车,从始发站北京南站到终点站海虹桥站,约需要多少小时(结果保留小数点后一位)?
1318÷300≈4.4(h)
(2)京沪高铁列车的行程y(单位:km)与运行时间t(单位:h)之间有何数量关系?
y=300t(0≤t≤4.4)
(3)京沪高铁列车从北京南站出发2.5 h后,是否已经过了距始发站1 100 km的南京站?
y=300×2.5=750(km), 这是列车尚未 到 达 距 始 发 站 1 100km的南京站.
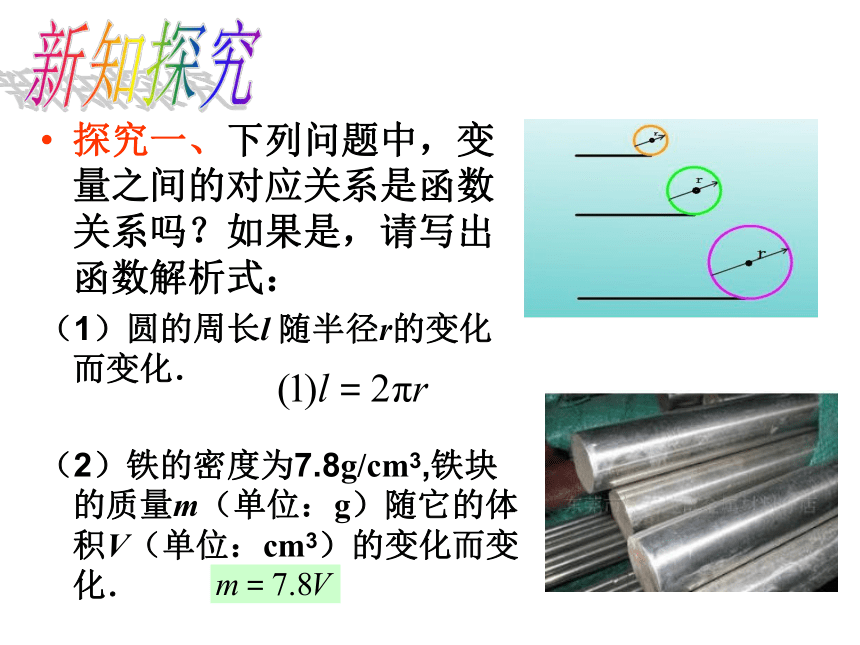
探究一、下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式:
(1)圆的周长l 随半径r的变化而变化.
(2)铁的密度为7.8g/cm3,铁块的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
(3)每个练习本的厚度为0.5cm,
一些练习本摞在一起的总厚度h
(单位:cm)随练习本的本数n的
变化而变化.
(4)冷冻一个0°C的物体,使它每
分钟下降2°C,物体问题T(单位:°C)
随冷冻时间t(单位:min)的变化而变
化.
(3)h=0.5n
(4)T=-2t
认真观察以上出现的四个函数解析式,分别说出哪些是函数、常数和自变量.
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
2π
r
l
h
T
t
0.5
-2
n
函数=常数×自变量
y
k
x
=
m
v
7.8
函数解析式 因变量 常量 自变量
l =2πr
m=7.8v
h = 0.5n
T = -2t
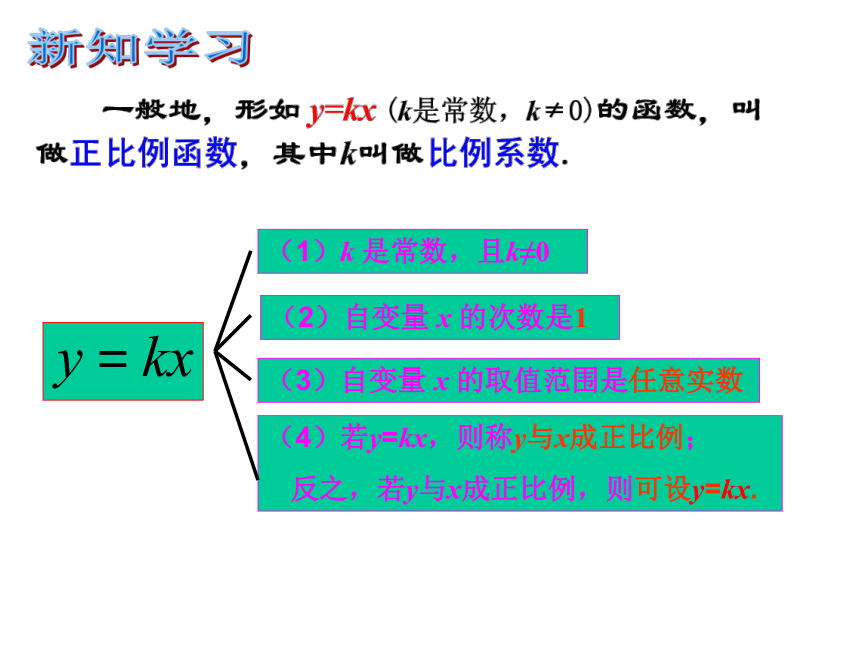
(1)k 是常数,且k≠0
(2)自变量 x 的次数是1
(3)自变量 x 的取值范围是任意实数
(4)若y=kx,则称y与x成正比例;
反之,若y与x成正比例,则可设y=kx.
下列函数中哪些是正比例函数?比例系数分别是什么?
(1)y =-0.1x (2) y= x
(3) y=2x2 (4)y2=4x
列示表示下列问题中的y与x的函数关系,并指出它是否是正比例函数。
(1)正方形的边长为xcm,周长为ycm;
(2)某人一年内的月平均收入为x元,他这年(12个月)的总收入为y元;
(3)一个长方体的长为2cm,宽为1.5cm,高为xcm,体积为ycm3。
y=4x
y=12x
y=3x
(1)若y=5x3m-2是正比例函数,则m= 。
更上一层楼!
(3)若 是正比例函数,则m= 。
注意:正比例函数的解析式要求
①比例系数不能是0。 ②自变量的指数是1。
1
±2
-2
(1)若 是正比例函数,则m= 。
(2)若 是正比例函数,则m= 。
3
-2
1.已知△ABC的底边BC=8cm,当BC边上的高从小到大变化时, △ABC的面积也随之变化。
(1)写出△ABC的面积y(cm2)与高线x的函数解析式,并指明它是什么函数;
(2)当x=7时,求出y的值。
(3)自己选择x的取值,并求y的值。
应用新知
2.已知:y与x成正比例,且x=4时,y=8,
(1)写出y与x之间的函数解析式;
(2)当x=2时,求y的值;
(3)当y=2时,求x的值。
解:设y=kx,
由题意得:8=4k
解得: k=2
答:所求函数解析式为y=2x
求正比例函数解析式的步骤:
(1)设
(2)列
(3)解
(4)答
如果y与x成正比例,且当x= 时,y=3,求y与x的函数关系式。
1、下列函数中 是正比例函数(填序号)
2、下列函数关系式中,属于正比例函数关系式的是( )
(A)圆的面积S与它的半径r
(B)行驶速度不变时,行驶路程S与时间t
(C)正方形的面积S与边长a
(D)工作总量(看作“1” )一定,工作效率w与工作时间t
3、已知:y与x成正比例,且x=1时,y=6。
求(1)y与x的函数解析式;
(2)当x=2时,求y的值。
小结
1、正比例函数的概念和解析式;
2、正比例函数的简单应用。
已知:y与x+3成正比例,且x=2时,y=-5。
求y与x的函数解析式;
老师寄语:
时间是一个“常量”,但对勤奋者来说是一个“变量”,我们应在有限的时间内做出伟大的事业!
我们在学业上的收获与我们平时的付出是“成正比”的,相信自己只要付出就一定有收获!
问题
2011年开始运营的京沪高速铁路全长1318千米
设列车的平均速度为300千米每小时。考虑以下问题:
(1)乘高铁,从始发站北京南站到终点站上海站,约需多少小时?(保留一位小数)
(2)京沪高铁的行程ykm与时间th之间有何数量关系?
(3)从北京南站出发2.5小时后是否已过了距始发站1100千米的南京南站?
(1)乘京沪高速列车,从始发站北京南站到终点站海虹桥站,约需要多少小时(结果保留小数点后一位)?
1318÷300≈4.4(h)
(2)京沪高铁列车的行程y(单位:km)与运行时间t(单位:h)之间有何数量关系?
y=300t(0≤t≤4.4)
(3)京沪高铁列车从北京南站出发2.5 h后,是否已经过了距始发站1 100 km的南京站?
y=300×2.5=750(km), 这是列车尚未 到 达 距 始 发 站 1 100km的南京站.
探究一、下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式:
(1)圆的周长l 随半径r的变化而变化.
(2)铁的密度为7.8g/cm3,铁块的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
(3)每个练习本的厚度为0.5cm,
一些练习本摞在一起的总厚度h
(单位:cm)随练习本的本数n的
变化而变化.
(4)冷冻一个0°C的物体,使它每
分钟下降2°C,物体问题T(单位:°C)
随冷冻时间t(单位:min)的变化而变
化.
(3)h=0.5n
(4)T=-2t
认真观察以上出现的四个函数解析式,分别说出哪些是函数、常数和自变量.
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
2π
r
l
h
T
t
0.5
-2
n
函数=常数×自变量
y
k
x
=
m
v
7.8
函数解析式 因变量 常量 自变量
l =2πr
m=7.8v
h = 0.5n
T = -2t
(1)k 是常数,且k≠0
(2)自变量 x 的次数是1
(3)自变量 x 的取值范围是任意实数
(4)若y=kx,则称y与x成正比例;
反之,若y与x成正比例,则可设y=kx.
下列函数中哪些是正比例函数?比例系数分别是什么?
(1)y =-0.1x (2) y= x
(3) y=2x2 (4)y2=4x
列示表示下列问题中的y与x的函数关系,并指出它是否是正比例函数。
(1)正方形的边长为xcm,周长为ycm;
(2)某人一年内的月平均收入为x元,他这年(12个月)的总收入为y元;
(3)一个长方体的长为2cm,宽为1.5cm,高为xcm,体积为ycm3。
y=4x
y=12x
y=3x
(1)若y=5x3m-2是正比例函数,则m= 。
更上一层楼!
(3)若 是正比例函数,则m= 。
注意:正比例函数的解析式要求
①比例系数不能是0。 ②自变量的指数是1。
1
±2
-2
(1)若 是正比例函数,则m= 。
(2)若 是正比例函数,则m= 。
3
-2
1.已知△ABC的底边BC=8cm,当BC边上的高从小到大变化时, △ABC的面积也随之变化。
(1)写出△ABC的面积y(cm2)与高线x的函数解析式,并指明它是什么函数;
(2)当x=7时,求出y的值。
(3)自己选择x的取值,并求y的值。
应用新知
2.已知:y与x成正比例,且x=4时,y=8,
(1)写出y与x之间的函数解析式;
(2)当x=2时,求y的值;
(3)当y=2时,求x的值。
解:设y=kx,
由题意得:8=4k
解得: k=2
答:所求函数解析式为y=2x
求正比例函数解析式的步骤:
(1)设
(2)列
(3)解
(4)答
如果y与x成正比例,且当x= 时,y=3,求y与x的函数关系式。
1、下列函数中 是正比例函数(填序号)
2、下列函数关系式中,属于正比例函数关系式的是( )
(A)圆的面积S与它的半径r
(B)行驶速度不变时,行驶路程S与时间t
(C)正方形的面积S与边长a
(D)工作总量(看作“1” )一定,工作效率w与工作时间t
3、已知:y与x成正比例,且x=1时,y=6。
求(1)y与x的函数解析式;
(2)当x=2时,求y的值。
小结
1、正比例函数的概念和解析式;
2、正比例函数的简单应用。
已知:y与x+3成正比例,且x=2时,y=-5。
求y与x的函数解析式;
老师寄语:
时间是一个“常量”,但对勤奋者来说是一个“变量”,我们应在有限的时间内做出伟大的事业!
我们在学业上的收获与我们平时的付出是“成正比”的,相信自己只要付出就一定有收获!
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
