北师大版八年级下册数学1.2 直角三角形全等的判定课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级下册数学1.2 直角三角形全等的判定课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
1.2 直角三角形
第一章 三角形的证明
北师大版 数学八年级下 册
第2课时 直角三角形全等的判定
等边对等角.
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
作底边中线.
温故知新:
SSS
作顶角平分线.
SAS
张家口市第九中学
等腰三角形的两底角相等.
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
作底边中线.
作顶角平分线.
作底边上的高线.
┓
温故知新:
张家口市第九中学
┓
异思妙想:
5
5
4
Rt△ABD≌Rt△ACD
D
AD=AD
AB=AC
∠D=∠D
但△ABD和△ACD不全等
张家口市第九中学
3
3
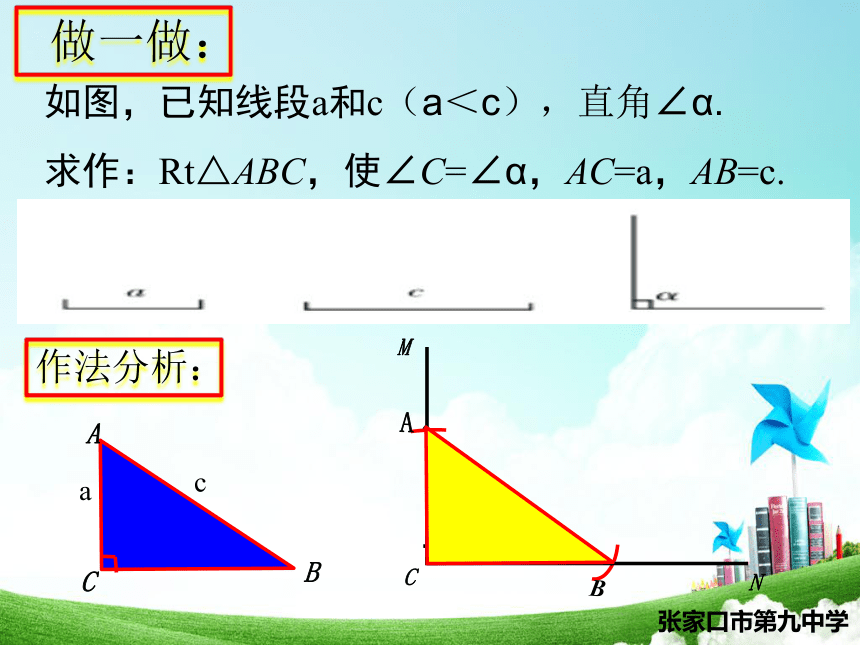
如图,已知线段a和c(a<c),直角∠α.
求作:Rt△ABC,使∠C=∠α,AC=a,AB=c.
做一做:
张家口市第九中学
作法分析:
把画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系?
发现:Rt△ABC≌Rt△A?B?C?
通过探究,由此你是否发现判定直角三角形全等的一种“特有”方法?尝试用数学语言归纳、概括由此获得的猜想。
探索与发现:
猜想: 和 对应相等
的两个直角三角形全等。
斜边
一条直角边
张家口市第九中学
已知:如图,在ΔABC和ΔA'B'C'中,
∠C=∠C'=900, AB=A'B', AC=A'C'.
求证:ΔABC≌ΔA'B'C'
猜想与验证:
和 对应相等的两个
直角三角形全等。
张家口市第九中学
斜边
一条直角边
证明:在ΔABC中,
∵ ∠C=90°
验证猜想:
∴ BC? = AB? - AC?
∵ AB=A'B',AC=A'C'
同理B'C'? = A'B'? -A'C'?
∴ΔABC ≌ ΔA'B'C'
∴ BC? = B'C'?
又∵BC>0,B'C'>0
∴ BC = B'C'
张家口市第九中学
(SAS)
(SSS)
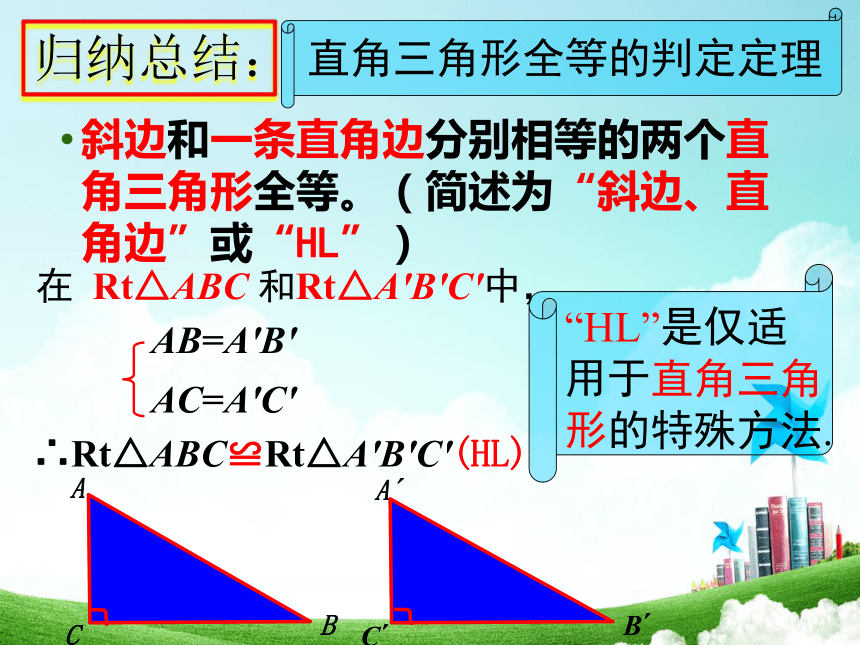
斜边和一条直角边分别相等的两个直角三角形全等。(简述为“斜边、直角边”或“HL”)
归纳总结:
在 Rt△ABC 和Rt△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'(HL)
直角三角形全等的判定定理
1、如图,AD⊥BD于D,AC⊥BC于C,要根据“HL”证明Rt△ABD≌△Rt△BAC,则还需要添加一个条件是 .
AD=BC
或 AC=BD
A
B
D
C
小试牛刀:
张家口市第九中学
2.下列条件,不能判定两个直角三角 形全等是( )
A.两条直角边对应相等
B.一个锐角和斜边对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
D
小试牛刀:
SAS
AAS
HL
张家口市第九中学
例1:如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:∠B+∠F=90°理由如下:
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF(全等三角形对应角相等).
∵ ∠DEF+∠F=90°
∴∠B+∠F=90°.
学以致用:
应用“HL”的前提条件是在直角三角形中.
规范应用“HL”判定方法的书写格式.
利用全等证明两个角相等,这是常见的思路.
张家口市第九中学
两个长度相同
由题意知:∠BAC=∠EDF=90°
③∵AE=CF, ∴AE+EF=CF+EF. 即AF=CE.
④∴BF=DE.
⑤∴ Rt△ABF≌Rt△CDE (HL).
② ∵ BF⊥AC,DE⊥AC, ∴∠BFA=∠DEC=90 °.
你认为证明步骤正确的顺序为 。
③
②
①
⑤
④
巩固与应用:
张家口市第九中学
AB=CD,
AF=CE,
2.如图,点A,E,F,C在同一直线上,AE=CF,过点E,F分别作 DE⊥AC,BF⊥AC,连接AB,CD,且AB=CD.
求证:BF=DE. 以下是排乱的证明过程:
② ③ ① ⑤④
1、已知:如图,AC、BD相交于点P,
AC⊥BC于C,BD⊥AD于D,且AD=BC.
求证:AC=BD.
一题多解 优化方案
张家口市第九中学
A
B
提升训练:
(2)在证明两个直角三角形全等时,其他方法都需要三个条件,而“HL”只有两个条件,你怎么看?
(1)判定两个直角三角形全等的方法有哪些?
(3)在课堂上,我们探究HL定理经历了怎样的过程?通过这个过程,你有什么感受和体会?
知识梳理 总结升华:
张家口市第九中学
“SSS”“SAS”“ASA”“AAS”“HL”
数学思想方法与策略:
例1':如图,有两个长度相同的滑梯EF、BC,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,把△EDF沿水平方向向左平移使得D与B重合,两个滑梯的位置关系如何?
例题再探:
张家口市第九中学
如图,已知Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q 两点分别在线段AC上和过A点且垂直于AC的射线AD上运动,问P点运动到什么位置时 PQ⊥AB?
勇攀高峰:
小明的解答过程如下:
解:当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),∴AP=BC=5cm;
答:当AP=5cm时,△ABC才能和△APQ 全等.
张家口市第九中学
D
△ABC才能和△APQ全等?
你同意小明的解答吗?说说你的想法。
【方法总结】判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
D
(P)
张家口市第九中学
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
证明:∵ ∠ACB=∠A'C'B'=90°
∴ B、C、B'三点共线
∵ AB=A'B', AC⊥BB'
∴ BC=B'C'(等腰三角形三线合一)
分析:AC=A'C',无论RTΔABC和RTΔA'B'C'的位置如何。我们总可以通过作旋转、平移、轴对称变换得到新图形,如图,使A'C'和AC重合,点B和点B'分别在AC的两侧。
定理证明再探:
张家口市第九中学
又∵ AC=A'C'(公共边)
∴ RTΔABC ≌ RTΔA'B'C'(SSS)
这节课----
回顾与感悟:
张家口市第九中学
我学会了……
我发现了……
使我感到最困难的是……
我想进一步研究的问题是……
本节课:我们有操作探究、猜想验证、合作交流、质疑批判、创新思考……
我想给同学们的温馨提示是……
张家口市第九中学
1.2 直角三角形
第一章 三角形的证明
北师大版 数学八年级下 册
第2课时 直角三角形全等的判定
等边对等角.
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
作底边中线.
温故知新:
SSS
作顶角平分线.
SAS
张家口市第九中学
等腰三角形的两底角相等.
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
作底边中线.
作顶角平分线.
作底边上的高线.
┓
温故知新:
张家口市第九中学
┓
异思妙想:
5
5
4
Rt△ABD≌Rt△ACD
D
AD=AD
AB=AC
∠D=∠D
但△ABD和△ACD不全等
张家口市第九中学
3
3
如图,已知线段a和c(a<c),直角∠α.
求作:Rt△ABC,使∠C=∠α,AC=a,AB=c.
做一做:
张家口市第九中学
作法分析:
把画好的直角三角形剪下来,和同桌的比比看,这些直角三角形有怎样的关系?
发现:Rt△ABC≌Rt△A?B?C?
通过探究,由此你是否发现判定直角三角形全等的一种“特有”方法?尝试用数学语言归纳、概括由此获得的猜想。
探索与发现:
猜想: 和 对应相等
的两个直角三角形全等。
斜边
一条直角边
张家口市第九中学
已知:如图,在ΔABC和ΔA'B'C'中,
∠C=∠C'=900, AB=A'B', AC=A'C'.
求证:ΔABC≌ΔA'B'C'
猜想与验证:
和 对应相等的两个
直角三角形全等。
张家口市第九中学
斜边
一条直角边
证明:在ΔABC中,
∵ ∠C=90°
验证猜想:
∴ BC? = AB? - AC?
∵ AB=A'B',AC=A'C'
同理B'C'? = A'B'? -A'C'?
∴ΔABC ≌ ΔA'B'C'
∴ BC? = B'C'?
又∵BC>0,B'C'>0
∴ BC = B'C'
张家口市第九中学
(SAS)
(SSS)
斜边和一条直角边分别相等的两个直角三角形全等。(简述为“斜边、直角边”或“HL”)
归纳总结:
在 Rt△ABC 和Rt△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'(HL)
直角三角形全等的判定定理
1、如图,AD⊥BD于D,AC⊥BC于C,要根据“HL”证明Rt△ABD≌△Rt△BAC,则还需要添加一个条件是 .
AD=BC
或 AC=BD
A
B
D
C
小试牛刀:
张家口市第九中学
2.下列条件,不能判定两个直角三角 形全等是( )
A.两条直角边对应相等
B.一个锐角和斜边对应相等
C.斜边和一条直角边对应相等
D.两个锐角对应相等
D
小试牛刀:
SAS
AAS
HL
张家口市第九中学
例1:如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解:∠B+∠F=90°理由如下:
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF(全等三角形对应角相等).
∵ ∠DEF+∠F=90°
∴∠B+∠F=90°.
学以致用:
应用“HL”的前提条件是在直角三角形中.
规范应用“HL”判定方法的书写格式.
利用全等证明两个角相等,这是常见的思路.
张家口市第九中学
两个长度相同
由题意知:∠BAC=∠EDF=90°
③∵AE=CF, ∴AE+EF=CF+EF. 即AF=CE.
④∴BF=DE.
⑤∴ Rt△ABF≌Rt△CDE (HL).
② ∵ BF⊥AC,DE⊥AC, ∴∠BFA=∠DEC=90 °.
你认为证明步骤正确的顺序为 。
③
②
①
⑤
④
巩固与应用:
张家口市第九中学
AB=CD,
AF=CE,
2.如图,点A,E,F,C在同一直线上,AE=CF,过点E,F分别作 DE⊥AC,BF⊥AC,连接AB,CD,且AB=CD.
求证:BF=DE. 以下是排乱的证明过程:
② ③ ① ⑤④
1、已知:如图,AC、BD相交于点P,
AC⊥BC于C,BD⊥AD于D,且AD=BC.
求证:AC=BD.
一题多解 优化方案
张家口市第九中学
A
B
提升训练:
(2)在证明两个直角三角形全等时,其他方法都需要三个条件,而“HL”只有两个条件,你怎么看?
(1)判定两个直角三角形全等的方法有哪些?
(3)在课堂上,我们探究HL定理经历了怎样的过程?通过这个过程,你有什么感受和体会?
知识梳理 总结升华:
张家口市第九中学
“SSS”“SAS”“ASA”“AAS”“HL”
数学思想方法与策略:
例1':如图,有两个长度相同的滑梯EF、BC,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,把△EDF沿水平方向向左平移使得D与B重合,两个滑梯的位置关系如何?
例题再探:
张家口市第九中学
如图,已知Rt△ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q 两点分别在线段AC上和过A点且垂直于AC的射线AD上运动,问P点运动到什么位置时 PQ⊥AB?
勇攀高峰:
小明的解答过程如下:
解:当P运动到AP=BC时,
∵∠C=∠QAP=90°.
在Rt△ABC与Rt△QPA中,
∵PQ=AB,AP=BC,
∴Rt△ABC≌Rt△QPA(HL),∴AP=BC=5cm;
答:当AP=5cm时,△ABC才能和△APQ 全等.
张家口市第九中学
D
△ABC才能和△APQ全等?
你同意小明的解答吗?说说你的想法。
【方法总结】判定三角形全等的关键是找对应边和对应角,由于本题没有说明全等三角形的对应边和对应角,因此要分类讨论,以免漏解.
D
(P)
张家口市第九中学
PPT模板:www.1ppt.com/moban/ PPT素材:www.1ppt.com/sucai/
PPT背景:www.1ppt.com/beijing/ PPT图表:www.1ppt.com/tubiao/
PPT下载:www.1ppt.com/xiazai/ PPT教程: www.1ppt.com/powerpoint/
资料下载:www.1ppt.com/ziliao/ 范文下载:www.1ppt.com/fanwen/
试卷下载:www.1ppt.com/shiti/ 教案下载:www.1ppt.com/jiaoan/
PPT论坛:www.1ppt.cn PPT课件:www.1ppt.com/kejian/
语文课件:www.1ppt.com/kejian/yuwen/ 数学课件:www.1ppt.com/kejian/shuxue/
英语课件:www.1ppt.com/kejian/yingyu/ 美术课件:www.1ppt.com/kejian/meishu/
科学课件:www.1ppt.com/kejian/kexue/ 物理课件:www.1ppt.com/kejian/wuli/
化学课件:www.1ppt.com/kejian/huaxue/ 生物课件:www.1ppt.com/kejian/shengwu/
地理课件:www.1ppt.com/kejian/dili/ 历史课件:www.1ppt.com/kejian/lishi/
证明:∵ ∠ACB=∠A'C'B'=90°
∴ B、C、B'三点共线
∵ AB=A'B', AC⊥BB'
∴ BC=B'C'(等腰三角形三线合一)
分析:AC=A'C',无论RTΔABC和RTΔA'B'C'的位置如何。我们总可以通过作旋转、平移、轴对称变换得到新图形,如图,使A'C'和AC重合,点B和点B'分别在AC的两侧。
定理证明再探:
张家口市第九中学
又∵ AC=A'C'(公共边)
∴ RTΔABC ≌ RTΔA'B'C'(SSS)
这节课----
回顾与感悟:
张家口市第九中学
我学会了……
我发现了……
使我感到最困难的是……
我想进一步研究的问题是……
本节课:我们有操作探究、猜想验证、合作交流、质疑批判、创新思考……
我想给同学们的温馨提示是……
张家口市第九中学
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
