北师大版八年级数学下册1.2.1直角三角形课件(共20张)
文档属性
| 名称 | 北师大版八年级数学下册1.2.1直角三角形课件(共20张) |  | |
| 格式 | zip | ||
| 文件大小 | 855.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 15:32:07 | ||
图片预览






文档简介
(共20张PPT)
1.能够证明直角三角形的性质定理和判定定理,进一步熟悉证明的基本步骤和书写格式,体会证明的必要性;
2.体验数学活动中的探索与创造,感受数学的严谨性.
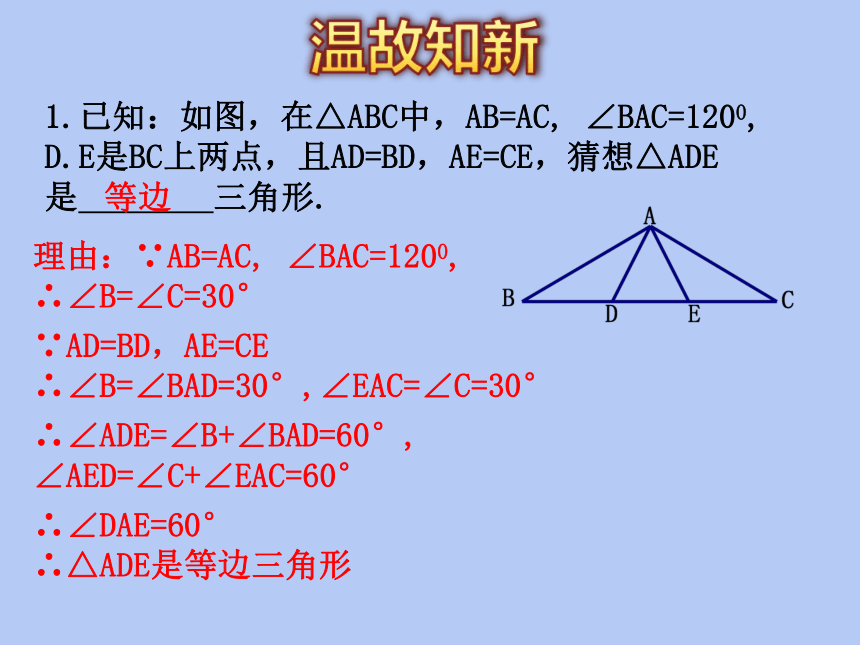
1.已知:如图,在△ABC中,AB=AC, ∠BAC=1200, D.E是BC上两点,且AD=BD,AE=CE,猜想△ADE
是 三角形.
理由:∵AB=AC, ∠BAC=1200,
∴∠B=∠C=30°
∵AD=BD,AE=CE
∴∠B=∠BAD=30°,∠EAC=∠C=30°
∴∠ADE=∠B+∠BAD=60°,
∠AED=∠C+∠EAC=60°
∴∠DAE=60°
∴△ADE是等边三角形
等边
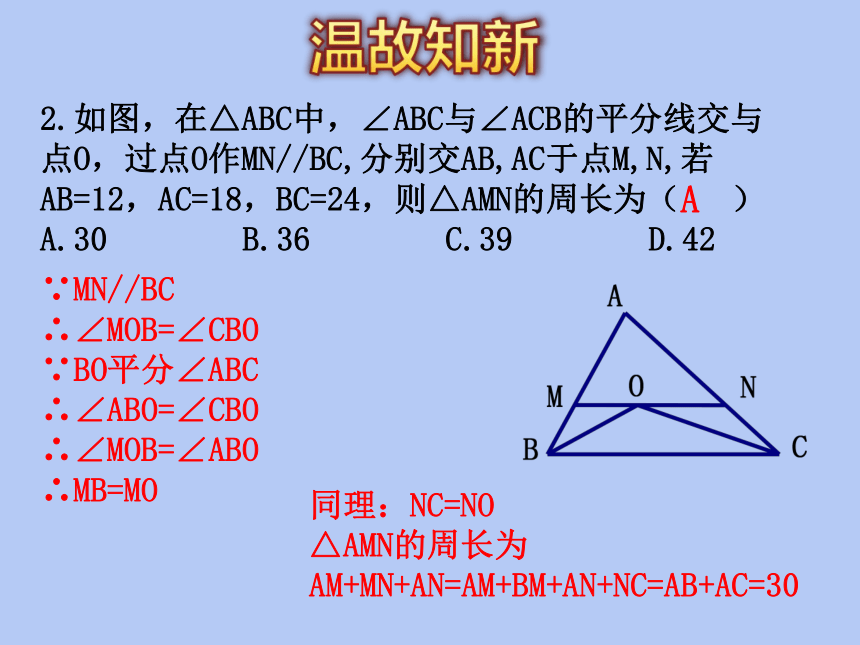
2.如图,在△ABC中,∠ABC与∠ACB的平分线交与点O,过点O作MN//BC,分别交AB,AC于点M,N,若AB=12,AC=18,BC=24,则△AMN的周长为( )
A.30 B.36 C.39 D.42
A
∵MN//BC
∴∠MOB=∠CBO
∵BO平分∠ABC
∴∠ABO=∠CBO
∴∠MOB=∠ABO
∴MB=MO
同理:NC=NO
△AMN的周长为AM+MN+AN=AM+BM+AN+NC=AB+AC=30
3.说出你知道的勾股数: ;
4.我们曾经用什么方法得到了勾股定理: 。
5.勾股定理的内容是:________________________;
它的条件是:_______________;
结论是:___________________ .
3.4.5; 6.8.10;5.12.13;
数格子法
等面积法
直角三角形两条直角边的平方和
等于斜边的平方
直角三角形
两条直角边的平方和等于斜边的平方
6.将勾股定理的条件和结论分别变成结论和条件,其内容是:
如果一个三角形两边的平方和等于第三边
的平方,那么这个三角形是直角三角形
想一想:
(1) 直角三角形的两个锐角有什么关系?
(2) 有两个锐角互余的三角形是直角三角形吗?
1、定理:直角三角形的两个锐角。
2、定理:有两个角互余的三角形是三角形。
3、勾股定理:直角三角形两条直角边的平方和等于斜边的平方。
在一个三角形中,当两边的平方和等于第三边的平方时,这个三角形是直角三角形吗?你能证明这个结论吗?请尝试分别写出已知、求证。(参阅课本第14-15页)
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
求证:△ABC是直角三角形
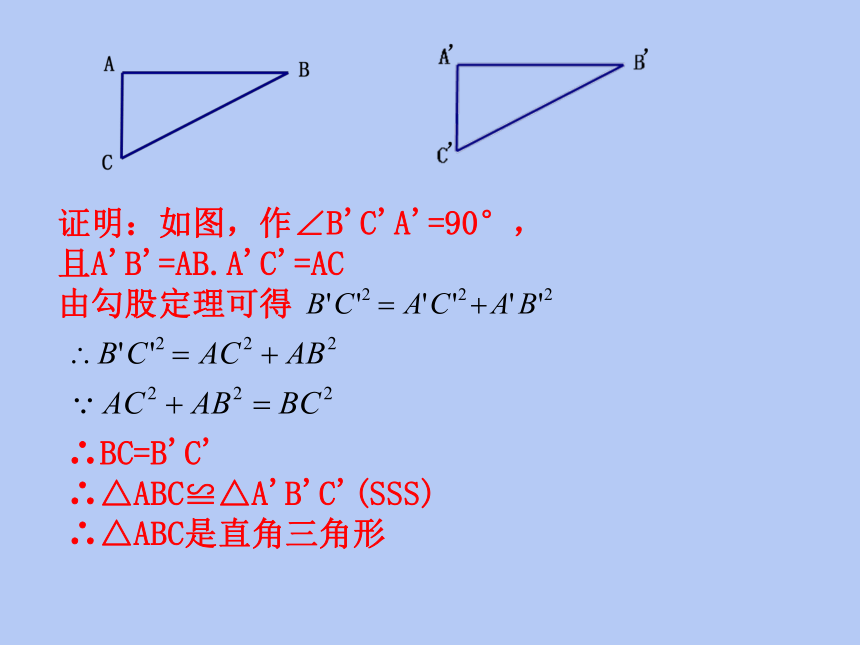
证明:如图,作∠B'C'A'=90°,
且A'B'=AB.A'C'=AC
由勾股定理可得
∴BC=B'C'
∴△ABC≌△A'B'C'(SSS)
∴△ABC是直角三角形
①一个命题是真命题,那么它的逆命题也一定是真命题吗?
②什么是互逆定理?是否任何定理都有逆定理?
③思考我们学过哪些互逆定理?
不一定
如果一个定理的逆命题也是真命题,那么这个命题就叫做原定理的逆定理,这两个定理叫做互逆定理,定理不一定都有逆定理
例1.判断对错:
A.每个命题都有逆命题,每个定理也都有逆定理.( )
B.命题正确时其逆命题也正确.( )
C.直角三角形两边分别是3,4,则第三边为5.( )
错
错
错
例2.下列长度的三条线段能构成直角三角形的是( )
①8,15,17 ②4,5,6
③7,5.4,8.5 ④ 24,25,7
⑤ 5,8,10
A.①②④ B.②④⑤
C.①③⑤ D.①③④
D
1、Rt△ABC中,∠C是直角,∠A=20°,则∠B= 。
2、△ABC中,∠C=35°,∠B=55°,则△ABC是 三角形。
3、如图,Rt△ABC中,∠C=90°,AC=2,BC=4,则AB= 。
70°
直角
A
D
6、写出命题“如果有两个有理数相等,那么它们的平方相等”的逆命题。
如果有两个有理数的平方相等,那么这两个有理数相等
本课知识:
1.直角三角形的判定定理:
;
2. 直角三角形的性质定理:
;
3.什么是互逆命题?
1.以下命题的逆命题属于假命题的是( )
A.两底角相等的两个三角形是等腰三角形.
B.全等三角形的对应角相等.
C.两直线平行,内错角相等.
D.直角三角形两锐角互等.
2.命题:等腰三角形两腰上的高相等的逆命题是____________.
B
如果一个三角形两边上的高相等,
那么这个三角形是等腰三角形
3.若一个直角两直角边之比为3:4,斜边长20CM,则两直角边为 .
4.已知直角三角形两直角边长分别为6和8,则斜边长为________,斜边上的高为_________.
12cm,16cm
10
4.8
5.台风过后,某小学旗杆在B处断裂,旗杆顶A落在离旗杆底部C点8M处,已知旗杆原长16M,则旗杆在距底部几米处断裂?
解:如图,AB+AC=16,设AC为x,AB=16-x
解得x=6
答:旗杆在距底部6米处断裂
6.小明将长2.5M的梯子斜靠在竖直的墙上,这时梯子底端B到墙根C的距离是0.7M,如果梯子的顶端垂直下滑0.4M,那么梯子的底端B将向外移动多少米.
解:在直角△ABC中,AB=2.5,BC=0.7
由勾股定理得AC=2.4
解得x= 0.8
答:梯子的底端B将向外移动0.8米
设BB’=x
在直角△A’B’C中,B’C=x+0.7,
A’B’=2.5, A’C=2.4=0.4=2
1.能够证明直角三角形的性质定理和判定定理,进一步熟悉证明的基本步骤和书写格式,体会证明的必要性;
2.体验数学活动中的探索与创造,感受数学的严谨性.
1.已知:如图,在△ABC中,AB=AC, ∠BAC=1200, D.E是BC上两点,且AD=BD,AE=CE,猜想△ADE
是 三角形.
理由:∵AB=AC, ∠BAC=1200,
∴∠B=∠C=30°
∵AD=BD,AE=CE
∴∠B=∠BAD=30°,∠EAC=∠C=30°
∴∠ADE=∠B+∠BAD=60°,
∠AED=∠C+∠EAC=60°
∴∠DAE=60°
∴△ADE是等边三角形
等边
2.如图,在△ABC中,∠ABC与∠ACB的平分线交与点O,过点O作MN//BC,分别交AB,AC于点M,N,若AB=12,AC=18,BC=24,则△AMN的周长为( )
A.30 B.36 C.39 D.42
A
∵MN//BC
∴∠MOB=∠CBO
∵BO平分∠ABC
∴∠ABO=∠CBO
∴∠MOB=∠ABO
∴MB=MO
同理:NC=NO
△AMN的周长为AM+MN+AN=AM+BM+AN+NC=AB+AC=30
3.说出你知道的勾股数: ;
4.我们曾经用什么方法得到了勾股定理: 。
5.勾股定理的内容是:________________________;
它的条件是:_______________;
结论是:___________________ .
3.4.5; 6.8.10;5.12.13;
数格子法
等面积法
直角三角形两条直角边的平方和
等于斜边的平方
直角三角形
两条直角边的平方和等于斜边的平方
6.将勾股定理的条件和结论分别变成结论和条件,其内容是:
如果一个三角形两边的平方和等于第三边
的平方,那么这个三角形是直角三角形
想一想:
(1) 直角三角形的两个锐角有什么关系?
(2) 有两个锐角互余的三角形是直角三角形吗?
1、定理:直角三角形的两个锐角。
2、定理:有两个角互余的三角形是三角形。
3、勾股定理:直角三角形两条直角边的平方和等于斜边的平方。
在一个三角形中,当两边的平方和等于第三边的平方时,这个三角形是直角三角形吗?你能证明这个结论吗?请尝试分别写出已知、求证。(参阅课本第14-15页)
如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
求证:△ABC是直角三角形
证明:如图,作∠B'C'A'=90°,
且A'B'=AB.A'C'=AC
由勾股定理可得
∴BC=B'C'
∴△ABC≌△A'B'C'(SSS)
∴△ABC是直角三角形
①一个命题是真命题,那么它的逆命题也一定是真命题吗?
②什么是互逆定理?是否任何定理都有逆定理?
③思考我们学过哪些互逆定理?
不一定
如果一个定理的逆命题也是真命题,那么这个命题就叫做原定理的逆定理,这两个定理叫做互逆定理,定理不一定都有逆定理
例1.判断对错:
A.每个命题都有逆命题,每个定理也都有逆定理.( )
B.命题正确时其逆命题也正确.( )
C.直角三角形两边分别是3,4,则第三边为5.( )
错
错
错
例2.下列长度的三条线段能构成直角三角形的是( )
①8,15,17 ②4,5,6
③7,5.4,8.5 ④ 24,25,7
⑤ 5,8,10
A.①②④ B.②④⑤
C.①③⑤ D.①③④
D
1、Rt△ABC中,∠C是直角,∠A=20°,则∠B= 。
2、△ABC中,∠C=35°,∠B=55°,则△ABC是 三角形。
3、如图,Rt△ABC中,∠C=90°,AC=2,BC=4,则AB= 。
70°
直角
A
D
6、写出命题“如果有两个有理数相等,那么它们的平方相等”的逆命题。
如果有两个有理数的平方相等,那么这两个有理数相等
本课知识:
1.直角三角形的判定定理:
;
2. 直角三角形的性质定理:
;
3.什么是互逆命题?
1.以下命题的逆命题属于假命题的是( )
A.两底角相等的两个三角形是等腰三角形.
B.全等三角形的对应角相等.
C.两直线平行,内错角相等.
D.直角三角形两锐角互等.
2.命题:等腰三角形两腰上的高相等的逆命题是____________.
B
如果一个三角形两边上的高相等,
那么这个三角形是等腰三角形
3.若一个直角两直角边之比为3:4,斜边长20CM,则两直角边为 .
4.已知直角三角形两直角边长分别为6和8,则斜边长为________,斜边上的高为_________.
12cm,16cm
10
4.8
5.台风过后,某小学旗杆在B处断裂,旗杆顶A落在离旗杆底部C点8M处,已知旗杆原长16M,则旗杆在距底部几米处断裂?
解:如图,AB+AC=16,设AC为x,AB=16-x
解得x=6
答:旗杆在距底部6米处断裂
6.小明将长2.5M的梯子斜靠在竖直的墙上,这时梯子底端B到墙根C的距离是0.7M,如果梯子的顶端垂直下滑0.4M,那么梯子的底端B将向外移动多少米.
解:在直角△ABC中,AB=2.5,BC=0.7
由勾股定理得AC=2.4
解得x= 0.8
答:梯子的底端B将向外移动0.8米
设BB’=x
在直角△A’B’C中,B’C=x+0.7,
A’B’=2.5, A’C=2.4=0.4=2
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
