沪科版七年级数学下册课件:8.3完全平方公式(第1课时) 课件(共20张PPT)
文档属性
| 名称 | 沪科版七年级数学下册课件:8.3完全平方公式(第1课时) 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 387.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
8.3完全平方公式
教学目标:
1、掌握完全平方公式。
2、运用几何图形推导完全公式。
3、通过解决实际问题,体会数学知识的应用价值
自学提纲:
1.阅读课本第64----65
2.完全平方公式的展开式是几次几项式 ?
交流:[1]怎样运用几何图形的面积来推导出完全平方公式?
(2)如何运用语言文字来叙述完全平方公式?
3.掌握完全平方公式结构特征。
4.完成下列计算(1)2x-y]2 (2)[3a-0.2b]2
5. 自学例1
完 全 平 方 公 式
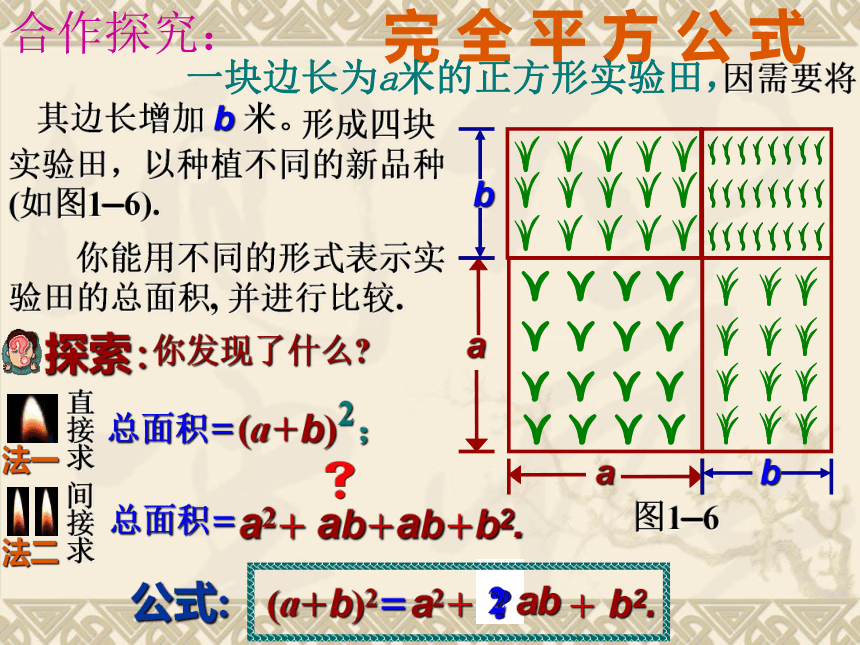
一块边长为a米的正方形实验田,
图1—6
因需要将其边长增加 b 米。
形成四块实验田,以种植不同的新品种(如图1—6).
你能用不同的形式表示实验田的总面积, 并进行比较.
(a+b) ;
2
a2+
ab+
ab+
b2.
(a+b)2=
a2+
ab
+
b2.
2
合作探究:
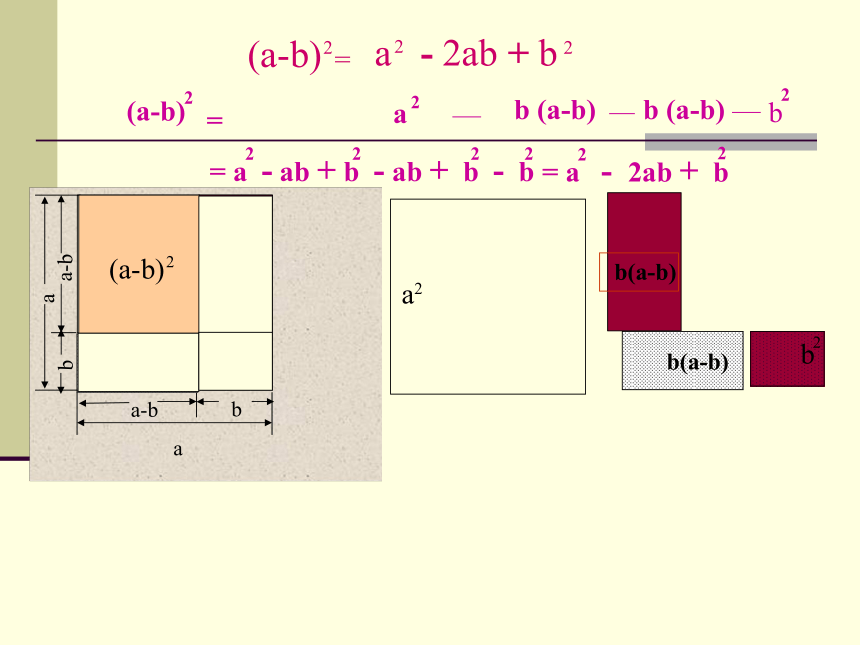
完全平方公式的证明
你能用多项式的乘法法则来说明它成立吗?
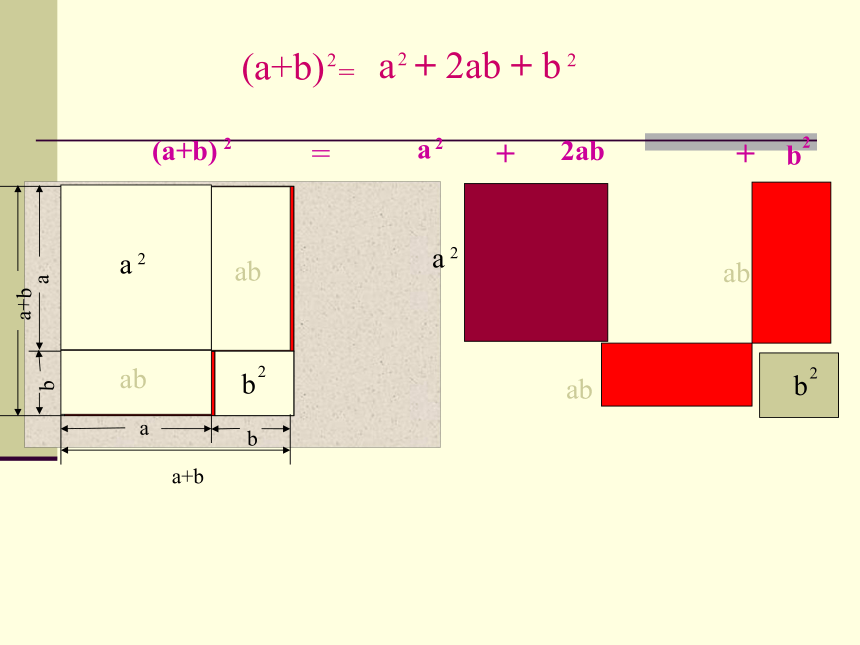
(a+b)2=a2+2ab+b2 ;
(a+b)2 =
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
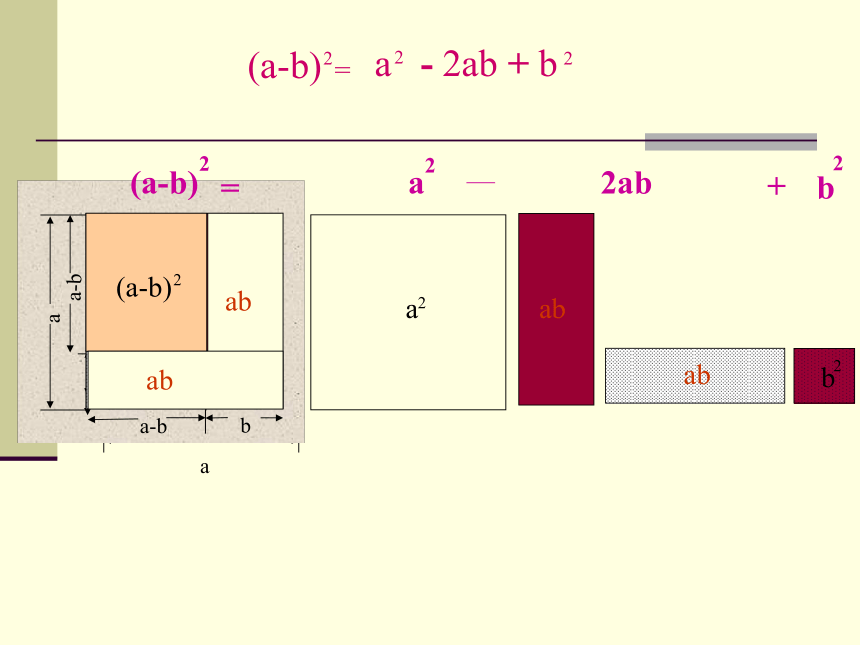
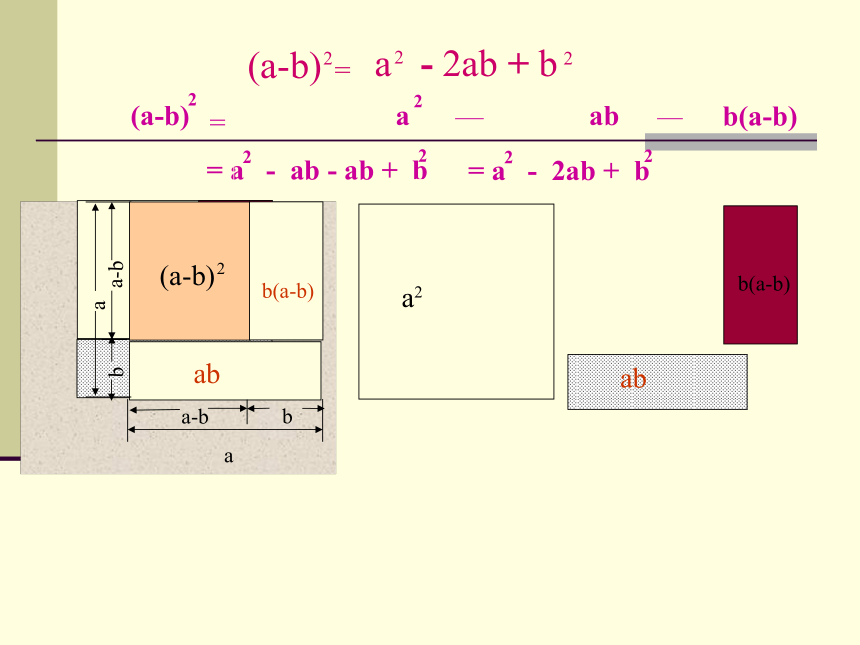
a2 ?2ab+b2.
?
(a?b)2=
=
+
2ab
+
ab
ab
b
ab
ab
=
2ab
+
ab
b(a-b)
=
ab
b(a-b)
b(a-b)
b(a-b)
b(a-b)
b(a-b)
=
b (a-b)
b (a-b)
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同。
首平方,末平方,首末两倍中间放
说一说
用自己的语言叙述上面的公式
语言表述:
两数和 的平方
等于
这两数的平方和
加上 这两数乘积的两倍.
(差)
(减去)
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
例1 运用完全平方公式计算:
解 (2x + y)2=
=4x2
(1)(2x+y)2
(a + b)2= a2 + 2 ab + b2
(2x)2
+2?2x ?y
+ y2
+ 4xy
+y2
例1 运用完全平方公式计算:
解: (3a-2b)2=
=9a2
(2)(3a-2b)2
(a - b)2= a2 - 2 ab + b2
(3a)2
-2?3a ?2b
+(2b)2
-12ab
+4b2
做一做:用两数和的完全平方公式计算(填空):
(a+1)2=( )2+2( )( )+( )2
=( )
(2)(2a - 3b)2=( )2 - 2( )( )+( )2
=( )
a
a
1
1
a2+2a+1
2a
2a
3b
3b
4a2 – 12ab + 9b2
1.(3x+7y)2 =
2.(-2a+3b)2=
算一算
今天是星期五,你知道992后的今天是星期几吗?
992=(100-1)2
=1002-2×100×1+12
=10000-200+1
=9801
9801÷7=1400……1
5022呢?
2 .多项式4x2+1加上一个单项式后能成为一个整式的完全平方,那么这个单项式是什么?
1. 观察下列各式:
152=225
252=625
352=1225
……
个位数字是5的两位数平方后,末尾的两个数有什么规律?为什么?
本节课你的收获是什么?
课堂:必做:习题8.3第1题 (1) (2)
第7题(1)(2)
选作:第2题(1) 第3题
家庭:基础训练同步
8.3完全平方公式
教学目标:
1、掌握完全平方公式。
2、运用几何图形推导完全公式。
3、通过解决实际问题,体会数学知识的应用价值
自学提纲:
1.阅读课本第64----65
2.完全平方公式的展开式是几次几项式 ?
交流:[1]怎样运用几何图形的面积来推导出完全平方公式?
(2)如何运用语言文字来叙述完全平方公式?
3.掌握完全平方公式结构特征。
4.完成下列计算(1)2x-y]2 (2)[3a-0.2b]2
5. 自学例1
完 全 平 方 公 式
一块边长为a米的正方形实验田,
图1—6
因需要将其边长增加 b 米。
形成四块实验田,以种植不同的新品种(如图1—6).
你能用不同的形式表示实验田的总面积, 并进行比较.
(a+b) ;
2
a2+
ab+
ab+
b2.
(a+b)2=
a2+
ab
+
b2.
2
合作探究:
完全平方公式的证明
你能用多项式的乘法法则来说明它成立吗?
(a+b)2=a2+2ab+b2 ;
(a+b)2 =
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
a2 ?2ab+b2.
?
(a?b)2=
=
+
2ab
+
ab
ab
b
ab
ab
=
2ab
+
ab
b(a-b)
=
ab
b(a-b)
b(a-b)
b(a-b)
b(a-b)
b(a-b)
=
b (a-b)
b (a-b)
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中
间的符号相同。
首平方,末平方,首末两倍中间放
说一说
用自己的语言叙述上面的公式
语言表述:
两数和 的平方
等于
这两数的平方和
加上 这两数乘积的两倍.
(差)
(减去)
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
下面各式的计算是否正确?如果不正确,应当怎样改正?
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
例1 运用完全平方公式计算:
解 (2x + y)2=
=4x2
(1)(2x+y)2
(a + b)2= a2 + 2 ab + b2
(2x)2
+2?2x ?y
+ y2
+ 4xy
+y2
例1 运用完全平方公式计算:
解: (3a-2b)2=
=9a2
(2)(3a-2b)2
(a - b)2= a2 - 2 ab + b2
(3a)2
-2?3a ?2b
+(2b)2
-12ab
+4b2
做一做:用两数和的完全平方公式计算(填空):
(a+1)2=( )2+2( )( )+( )2
=( )
(2)(2a - 3b)2=( )2 - 2( )( )+( )2
=( )
a
a
1
1
a2+2a+1
2a
2a
3b
3b
4a2 – 12ab + 9b2
1.(3x+7y)2 =
2.(-2a+3b)2=
算一算
今天是星期五,你知道992后的今天是星期几吗?
992=(100-1)2
=1002-2×100×1+12
=10000-200+1
=9801
9801÷7=1400……1
5022呢?
2 .多项式4x2+1加上一个单项式后能成为一个整式的完全平方,那么这个单项式是什么?
1. 观察下列各式:
152=225
252=625
352=1225
……
个位数字是5的两位数平方后,末尾的两个数有什么规律?为什么?
本节课你的收获是什么?
课堂:必做:习题8.3第1题 (1) (2)
第7题(1)(2)
选作:第2题(1) 第3题
家庭:基础训练同步
