湘教版七年级数学下学期 2.1.2幂的乘方与积的乘方课件(共22张PPT)
文档属性
| 名称 | 湘教版七年级数学下学期 2.1.2幂的乘方与积的乘方课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 323.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
2.1.3 积的乘方
名言:
聪明在于学习,天才在于积累。
所谓天才,实际上是依靠学习。
—— 华罗庚
回顾 & 思考
?
?
同底数幂的乘法运算法则:
am · an
=
?
am+n
(m,n都是正整数)
幂的乘方运算法则:
?
(am)n= (m、n都是正整数)
amn
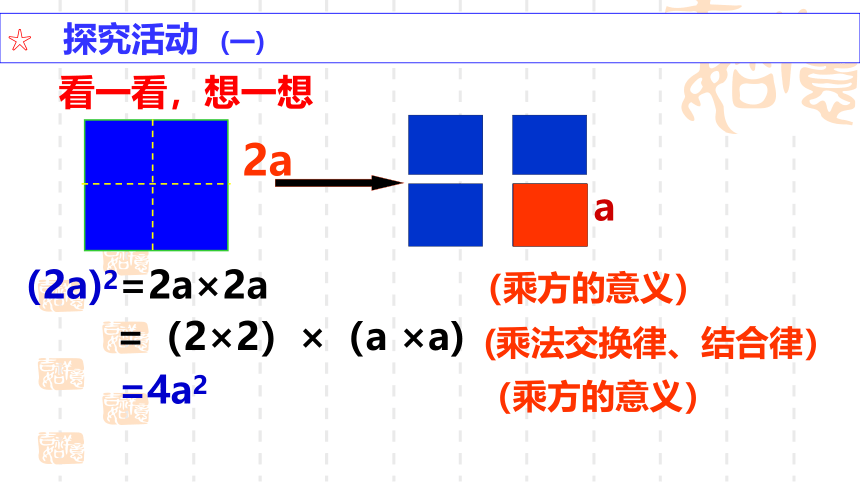
看一看,想一想
a
2a
☆ 探究活动 (一)
(2a)2=2a×2a
(乘方的意义)
=(2×2)×(a ×a)
(乘法交换律、结合律)
=4a2
(乘方的意义)
(1)
(2)
这两个题目的底数有什么特点?
底数为两个因式相乘,积的形式。
这种形式为积的乘方
☆ 探究活动 (二)
观察、猜想
同理:
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
交流与发现:积的乘方(ab)n =?
(2m)4
=(2×2×2×2). (m.m.m.m)
=24m4=16m4
=(2m).(2m).(2m).(2m)
(ab) n= (ab)· (ab)· ··· ·(ab)
n个(ab)
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn
证明:
积的乘方(ab)n =?
结论:
(ab)n=anbn (n为正整数)
推广:三个或三个以上的积的乘方等于什么?
(abc)n
(a b)n = an bn (n为正整数)
积的乘方的运算法则:
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
= anbncn (n为正整数)
结果是多少呢?
简记:积的乘方=乘方的积
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-2a2)2=-4a4 ( )
(4) (-ab2c)2=a2b4c ( )
判断:
(5) ( )
×
大家来找茬!
(1) (-2a)2 (2) (-5ab)3
(3) (-x3y3)2 + (-3x2y2)3
例题解析
例题分析:
P34 例6 、例7
注意: (1)括号内每一个因式都要乘方,包括系数。
(“兄弟分家要公平”)
(2)底数有负号、分数、幂的乘方运算,要打括号,
符号要奇负偶正。
(3) 运算顺序:先乘方,再乘法,后加减。
(4)结果要化简,有同类项的要合并。
1.计算:
(1)(-3x2y3)3
(2) (-2a3b2c)4
当堂训练
2、计算:
2(x3)2 · x3-(-3x3)3+(-5x)2 ·x7
积的乘方公式逆用可写为:
an bn = (a b)n (n为正整数)
(ab)n = anbn (n为正整数)
0.25100×4100=( )100
0.25×4
0.25100×4101=?
如何计算简便?
底数互为倒数或相乘可凑整的用此公式较简单
探讨--如何计算简便?
(0.04)2004×[(-5)2004]2=?
=(0.22)2004 × 54008
=(0.2)4008 × 54008
=(0.2 ×5)4008
=14008
解法一: 原式
=1
探讨--如何计算简便?
=(0.04)2004 × [(-5)2]2004
=(0.04×25)2004
=12004
=1
= (0.04)2004 ×252004
解法二: 原式
1
a
都要转化为( )n×an的形式
说明:逆用积的乘方法则 anbn = (ab)n可以
能力提升
如果(an?bm?b)3=a9b15,求m, n的值。
? (an)3?(bm)3?b3=a9b15
? a 3n ?b 3m?b3=a9b15
? a 3n ?b 3m+3=a9b15
? 3n=9 3m+3=15
?n=3,m=4.
解: (an?bm?b)3=a9b15
?
能力提升
若m=74,n=65,试用含m,n的代数式
表示8440.
小结:
1、本节课的主要内容:
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)
2、 运用积的乘方法则时要注意什么?
公式中的a、b代表任何代数式;每一个因式 都要“乘方”;注意结果的符号、幂指数及其逆向运用。(混合运算要注意运算顺序)
积的乘方
幂的运算的三条重要性质:
同底数幂的乘法、幂的乘方、积的乘方的区别:
同底数幂的乘法
幂的乘方
am·an
=am+n
(am)n
=amn
m、n为
正整数
(ab)n
=anbn
积的乘方
填空:
①(-2ab2)3=——— ②(-2a2b3c)4=————
③( )2×162=———④(-2a3b4)3=————
⑤若(5m)2=100,求m
⑥若am=2,an=3,求a3m+2n
1
4
⑦若2x=3,2y=1,求22x+y+1
⑧若 求m,n.
⑨求
-8
5
13
1
32
你是最棒的
用简便方法计算:
2.1.3 积的乘方
名言:
聪明在于学习,天才在于积累。
所谓天才,实际上是依靠学习。
—— 华罗庚
回顾 & 思考
?
?
同底数幂的乘法运算法则:
am · an
=
?
am+n
(m,n都是正整数)
幂的乘方运算法则:
?
(am)n= (m、n都是正整数)
amn
看一看,想一想
a
2a
☆ 探究活动 (一)
(2a)2=2a×2a
(乘方的意义)
=(2×2)×(a ×a)
(乘法交换律、结合律)
=4a2
(乘方的意义)
(1)
(2)
这两个题目的底数有什么特点?
底数为两个因式相乘,积的形式。
这种形式为积的乘方
☆ 探究活动 (二)
观察、猜想
同理:
(乘方的意义)
(乘法交换律、结合律)
(乘方的意义)
交流与发现:积的乘方(ab)n =?
(2m)4
=(2×2×2×2). (m.m.m.m)
=24m4=16m4
=(2m).(2m).(2m).(2m)
(ab) n= (ab)· (ab)· ··· ·(ab)
n个(ab)
=(a·a· ··· ·a)·(b·b· ··· ·b)
n个a
n个b
=anbn
证明:
积的乘方(ab)n =?
结论:
(ab)n=anbn (n为正整数)
推广:三个或三个以上的积的乘方等于什么?
(abc)n
(a b)n = an bn (n为正整数)
积的乘方的运算法则:
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
= anbncn (n为正整数)
结果是多少呢?
简记:积的乘方=乘方的积
(1)(ab2)3=ab6 ( )
×
×
×
(2) (3xy)3=9x3y3 ( )
×
(3) (-2a2)2=-4a4 ( )
(4) (-ab2c)2=a2b4c ( )
判断:
(5) ( )
×
大家来找茬!
(1) (-2a)2 (2) (-5ab)3
(3) (-x3y3)2 + (-3x2y2)3
例题解析
例题分析:
P34 例6 、例7
注意: (1)括号内每一个因式都要乘方,包括系数。
(“兄弟分家要公平”)
(2)底数有负号、分数、幂的乘方运算,要打括号,
符号要奇负偶正。
(3) 运算顺序:先乘方,再乘法,后加减。
(4)结果要化简,有同类项的要合并。
1.计算:
(1)(-3x2y3)3
(2) (-2a3b2c)4
当堂训练
2、计算:
2(x3)2 · x3-(-3x3)3+(-5x)2 ·x7
积的乘方公式逆用可写为:
an bn = (a b)n (n为正整数)
(ab)n = anbn (n为正整数)
0.25100×4100=( )100
0.25×4
0.25100×4101=?
如何计算简便?
底数互为倒数或相乘可凑整的用此公式较简单
探讨--如何计算简便?
(0.04)2004×[(-5)2004]2=?
=(0.22)2004 × 54008
=(0.2)4008 × 54008
=(0.2 ×5)4008
=14008
解法一: 原式
=1
探讨--如何计算简便?
=(0.04)2004 × [(-5)2]2004
=(0.04×25)2004
=12004
=1
= (0.04)2004 ×252004
解法二: 原式
1
a
都要转化为( )n×an的形式
说明:逆用积的乘方法则 anbn = (ab)n可以
能力提升
如果(an?bm?b)3=a9b15,求m, n的值。
? (an)3?(bm)3?b3=a9b15
? a 3n ?b 3m?b3=a9b15
? a 3n ?b 3m+3=a9b15
? 3n=9 3m+3=15
?n=3,m=4.
解: (an?bm?b)3=a9b15
?
能力提升
若m=74,n=65,试用含m,n的代数式
表示8440.
小结:
1、本节课的主要内容:
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都是正整数)
2、 运用积的乘方法则时要注意什么?
公式中的a、b代表任何代数式;每一个因式 都要“乘方”;注意结果的符号、幂指数及其逆向运用。(混合运算要注意运算顺序)
积的乘方
幂的运算的三条重要性质:
同底数幂的乘法、幂的乘方、积的乘方的区别:
同底数幂的乘法
幂的乘方
am·an
=am+n
(am)n
=amn
m、n为
正整数
(ab)n
=anbn
积的乘方
填空:
①(-2ab2)3=——— ②(-2a2b3c)4=————
③( )2×162=———④(-2a3b4)3=————
⑤若(5m)2=100,求m
⑥若am=2,an=3,求a3m+2n
1
4
⑦若2x=3,2y=1,求22x+y+1
⑧若 求m,n.
⑨求
-8
5
13
1
32
你是最棒的
用简便方法计算:
