湘教版七年级数学下册 2.1.4 多项式的乘法课件(共15张PPT)
文档属性
| 名称 | 湘教版七年级数学下册 2.1.4 多项式的乘法课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 952.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
1、我们学了“幂的运算性质”有哪些?
(m、n都是正整数)
2、单项式乘以多项式的法则是什么?
知识 & 回顾
下图是厨房的平面布局,你能用几种方法表示此厨房的总面积?
(1) 整体计算:
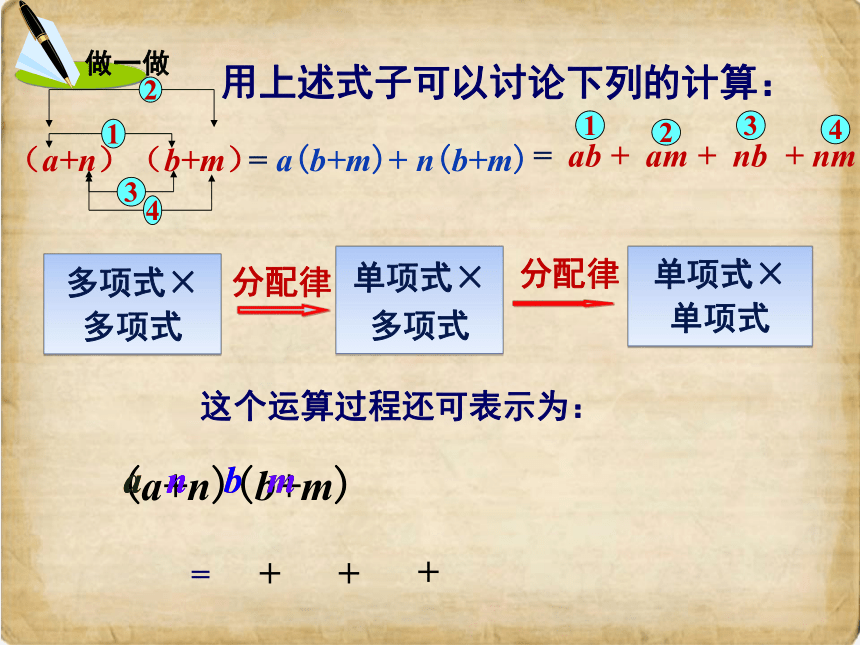
(a+n)(b+m)
(2) 左右计算:
a(b+m)+n(b+m)
(3) 分四部分计算:
ab+am+nb+nm
思考:三种方法计算的结果有什么关系?
即:(a+n)(b+m)= a(b+m)+n(b+m)= ab+am+nb+nm
相等
(a+n)(b+m)
= ab + am + nb + nm
多项式×多项式
单项式×多项式
单项式×单项式
1
2
3
4
= a(b+m)+ n(b+m)
这个运算过程还可表示为:
(a+n)(b+m)
=
a
b
+
a
m
+
n
b
n
+
m
用上述式子可以讨论下列的计算:
多项式乘以多项式,展开后项数有什么规律?
多项式乘法法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即(a+n)(b+m)=ab+am+nb+nm.
知识 & 归纳
(1) (2x+y)(x-3y)
解:(2x+y)(x-3y)
= 2x·x+2x·(-3y)+y·x+y ·(-3y)
= 2x2-6xy+yx-3y2
= 2x2-5xy-3y2
例1 计算:
(2)( 2x+1)(3x2-x-5);
解 :(2x+1)(3x2-x-5)
= 6x3-2x2–10x+3x2 -x-5
= 6x3 + x2-11x - 5.
(3)(x+a)(x+b)
解 :(x+a)(x+b)
= x2+bx+ax+ab
=x2+(a+b)x +ab
第(3)小题的直观意义如图
知识 & 巩固
(1)(3a-b)(2a+b)
解原式=3a ·2a+(-b)· b
= 6a2-b2;
1. 下列计算对不对?如果不对,应怎样改正?
(2)(x+3)(1-x)
解原式=x· 1+x·x+3-3·x
= x2 -2x+3.
答:不对,错在“漏乘”.正确答案为:6a2+ab-b2.
答:不对,错在二次项的系数。答案为:-x2-2x+3
例2 计算:
(1)(a-b)2.
解: (a-b)2
= (a-b)(a-b)
= a2-ab-ba+b2
= a2-2ab+b2
(2)(x+y)(x2-xy+y2)
解:(x+y)(x2-xy+y2)
= x3-x2y+xy2+x2y-xy2+y3
= x3+y3
(3)(a2+3)(a-2)-a(a2-2a-2).
5a-6
(4)2(x-8)(x-5)-(2x-1)(x+2)
-29x+82
1、解方程
2(x-3)(x+5)=x2 +(x-2)+(x-2)(x+3).
2.若(x2 +nx+3)(x2 -3x+m)的展开式中不含x2 和x3 的项,求m和n的值
拓展练习
(1)若(2x+3)(x+m)=2x2+5x-n,
则m= ,n= .
(2)当m=-3时,(2m-3)(3m+4)的值是_______.
(4)计算:(1)(x-1)(x+1)= ;
(2)(2a-5b)(a+5b)= .
1
-3
x2-1
2a2+5ab-25b2
2、填空:
45
(3)当x=-7时,代数式
(2x+5)(x+1)-(x-3)(x+1)的值为________.
-6
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.
注意:(1)多项式与多项式相乘的结果仍是多项式;
(2)结果的项数应该是原两个多项式项数的积(没有合并同类项之前),检验项数常常作为检验解题过程是否的有效方法.
(3)多项式与多项式相乘的结果中,要把同类项合并;
多项式乘法法则
课堂小结
(x+2)(x+3)=x2+5x+6;
(x+4)(x+2)=x2+6x+8;
(x+6)(x+5)=x2+11x+30.
3
5
3
5
观察下列各式的计算结果与相乘的两个多项式之间的关系:
(x+3)(x+5)=x2+( + )x + ×
(1)你发现有什么规律?按你发现的规律填空:
(2)你能很快说出与(x+a)(x+b)相等的多项式吗?
(x+a)(x+b)=x2+(a+b)x+ab
知识 & 提升
1. 确定下列各式中m与p的值(p,q为正整数):
(1)(x+4)(x+9)=x2 +mx+36
m=13
m=-20 n=36
p=12,m=15
p=6,m=-12
(2)(x-2)(x-18)=x2 +mx+n
(3)(x+3)(x+p)=x2 +mx+36
(4)(x-6)(x-p)=x2 +mx+36
快速&反应
2. 若(x+a)(x+b)的积中不含x的一次项,则a、b一定满足( )
A、互为倒数 B、互为相反数C、a=b=0 D、ab=0
B
4. 观察下列各式:
(x-1)(x+1)=x2-1 (x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1…根据前面各式的规律可得:(x-1)(xn+xn-1+xn-2+…+x+1)=________
xn+1-1
3. 有一长方形耕地,现要在该耕地上种植两块防风带,如图所示的黑色部分,其中横向防风带为长方形,纵向防风带为平行四边形,则剩余耕地面积为( )
A、bc-ab+ac+c2 B、ab-bc-ac+c2
C、a2+ab+bc-ac D、b2-bc+a2-ab
B
1、我们学了“幂的运算性质”有哪些?
(m、n都是正整数)
2、单项式乘以多项式的法则是什么?
知识 & 回顾
下图是厨房的平面布局,你能用几种方法表示此厨房的总面积?
(1) 整体计算:
(a+n)(b+m)
(2) 左右计算:
a(b+m)+n(b+m)
(3) 分四部分计算:
ab+am+nb+nm
思考:三种方法计算的结果有什么关系?
即:(a+n)(b+m)= a(b+m)+n(b+m)= ab+am+nb+nm
相等
(a+n)(b+m)
= ab + am + nb + nm
多项式×多项式
单项式×多项式
单项式×单项式
1
2
3
4
= a(b+m)+ n(b+m)
这个运算过程还可表示为:
(a+n)(b+m)
=
a
b
+
a
m
+
n
b
n
+
m
用上述式子可以讨论下列的计算:
多项式乘以多项式,展开后项数有什么规律?
多项式乘法法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.即(a+n)(b+m)=ab+am+nb+nm.
知识 & 归纳
(1) (2x+y)(x-3y)
解:(2x+y)(x-3y)
= 2x·x+2x·(-3y)+y·x+y ·(-3y)
= 2x2-6xy+yx-3y2
= 2x2-5xy-3y2
例1 计算:
(2)( 2x+1)(3x2-x-5);
解 :(2x+1)(3x2-x-5)
= 6x3-2x2–10x+3x2 -x-5
= 6x3 + x2-11x - 5.
(3)(x+a)(x+b)
解 :(x+a)(x+b)
= x2+bx+ax+ab
=x2+(a+b)x +ab
第(3)小题的直观意义如图
知识 & 巩固
(1)(3a-b)(2a+b)
解原式=3a ·2a+(-b)· b
= 6a2-b2;
1. 下列计算对不对?如果不对,应怎样改正?
(2)(x+3)(1-x)
解原式=x· 1+x·x+3-3·x
= x2 -2x+3.
答:不对,错在“漏乘”.正确答案为:6a2+ab-b2.
答:不对,错在二次项的系数。答案为:-x2-2x+3
例2 计算:
(1)(a-b)2.
解: (a-b)2
= (a-b)(a-b)
= a2-ab-ba+b2
= a2-2ab+b2
(2)(x+y)(x2-xy+y2)
解:(x+y)(x2-xy+y2)
= x3-x2y+xy2+x2y-xy2+y3
= x3+y3
(3)(a2+3)(a-2)-a(a2-2a-2).
5a-6
(4)2(x-8)(x-5)-(2x-1)(x+2)
-29x+82
1、解方程
2(x-3)(x+5)=x2 +(x-2)+(x-2)(x+3).
2.若(x2 +nx+3)(x2 -3x+m)的展开式中不含x2 和x3 的项,求m和n的值
拓展练习
(1)若(2x+3)(x+m)=2x2+5x-n,
则m= ,n= .
(2)当m=-3时,(2m-3)(3m+4)的值是_______.
(4)计算:(1)(x-1)(x+1)= ;
(2)(2a-5b)(a+5b)= .
1
-3
x2-1
2a2+5ab-25b2
2、填空:
45
(3)当x=-7时,代数式
(2x+5)(x+1)-(x-3)(x+1)的值为________.
-6
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式中的每一项,再把所得的积相加.
注意:(1)多项式与多项式相乘的结果仍是多项式;
(2)结果的项数应该是原两个多项式项数的积(没有合并同类项之前),检验项数常常作为检验解题过程是否的有效方法.
(3)多项式与多项式相乘的结果中,要把同类项合并;
多项式乘法法则
课堂小结
(x+2)(x+3)=x2+5x+6;
(x+4)(x+2)=x2+6x+8;
(x+6)(x+5)=x2+11x+30.
3
5
3
5
观察下列各式的计算结果与相乘的两个多项式之间的关系:
(x+3)(x+5)=x2+( + )x + ×
(1)你发现有什么规律?按你发现的规律填空:
(2)你能很快说出与(x+a)(x+b)相等的多项式吗?
(x+a)(x+b)=x2+(a+b)x+ab
知识 & 提升
1. 确定下列各式中m与p的值(p,q为正整数):
(1)(x+4)(x+9)=x2 +mx+36
m=13
m=-20 n=36
p=12,m=15
p=6,m=-12
(2)(x-2)(x-18)=x2 +mx+n
(3)(x+3)(x+p)=x2 +mx+36
(4)(x-6)(x-p)=x2 +mx+36
快速&反应
2. 若(x+a)(x+b)的积中不含x的一次项,则a、b一定满足( )
A、互为倒数 B、互为相反数C、a=b=0 D、ab=0
B
4. 观察下列各式:
(x-1)(x+1)=x2-1 (x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1…根据前面各式的规律可得:(x-1)(xn+xn-1+xn-2+…+x+1)=________
xn+1-1
3. 有一长方形耕地,现要在该耕地上种植两块防风带,如图所示的黑色部分,其中横向防风带为长方形,纵向防风带为平行四边形,则剩余耕地面积为( )
A、bc-ab+ac+c2 B、ab-bc-ac+c2
C、a2+ab+bc-ac D、b2-bc+a2-ab
B
