19.2.2 平行四边形的性质课件(共20张PPT)
文档属性
| 名称 | 19.2.2 平行四边形的性质课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-19 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
第2课时 平行四边形对角线性质
沪科版 八年级下
19.2 平行四边形
新知导入
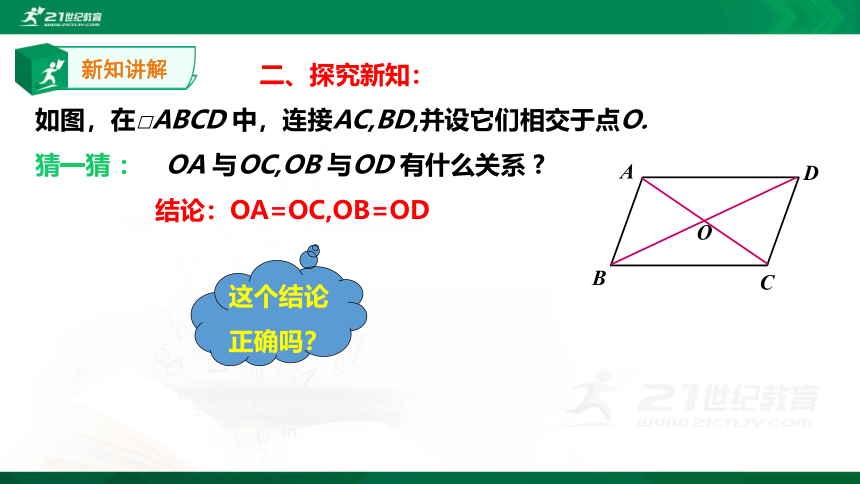
一、复习提问:
问题1.请叙述平行四边形的性质1?
平行四边形的性质1:平行四边形的对边相等.
问题2.请叙述平行四边形的性质2?
平行四边形的性质2:平行四边形的对角相等.
问题3.请问平行四边形还有什么性质呢?
新知讲解
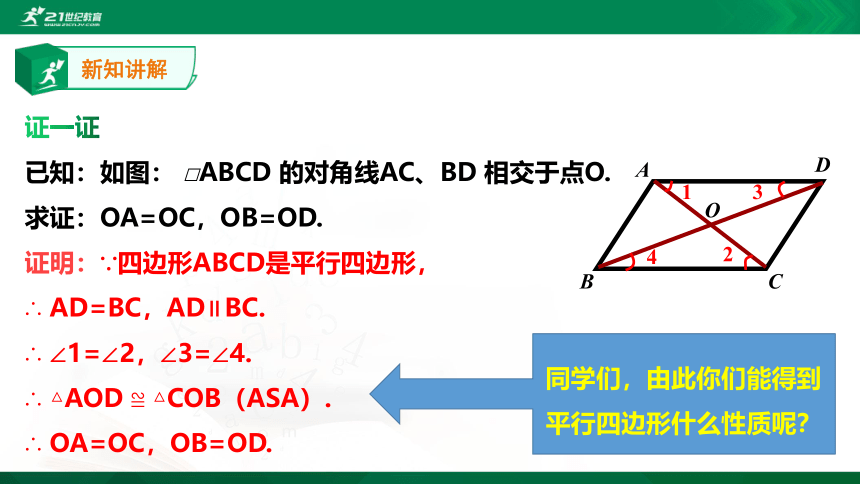
新知讲解
同学们,由此你们能得到平行四边形什么性质呢?
新知讲解
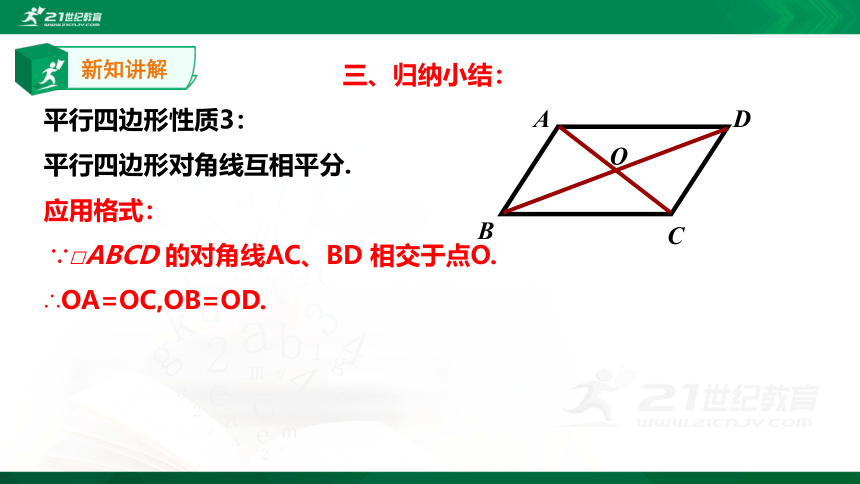
三、归纳小结:
平行四边形性质3:
平行四边形对角线互相平分.
应用格式:
∵□ABCD 的对角线AC、BD 相交于点O.
∴OA=OC,OB=OD.
新知讲解
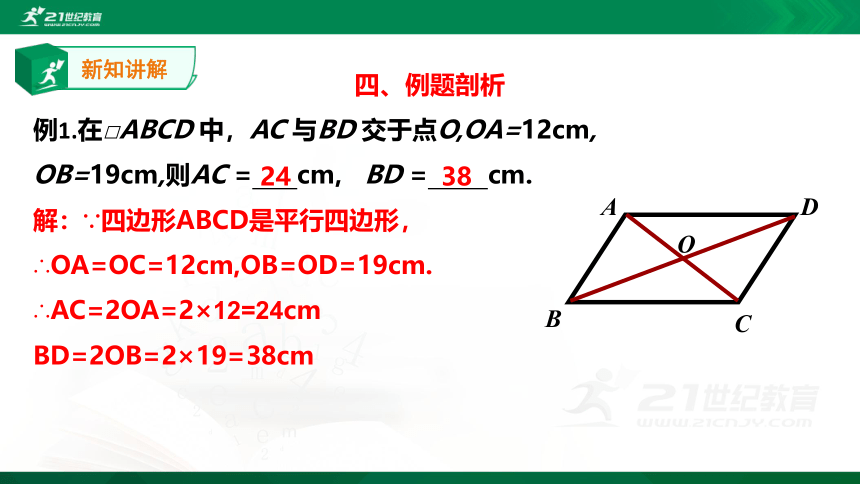
四、例题剖析
例1.在□ABCD 中,AC 与BD 交于点O,OA=12cm,
OB=19cm,则AC = cm, BD = cm.
解:∵四边形ABCD是平行四边形,
∴OA=OC=12cm,OB=OD=19cm.
∴AC=2OA=2×12=24cm
BD=2OB=2×19=38cm
24
38
新知讲解
例2.如图,平行四边形ABCD 中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
解:∵四边形ABCD是平行四边形,
∴BC=AD=5,
∵AB⊥AC,∴△ABC是直角三角形.
新知讲解
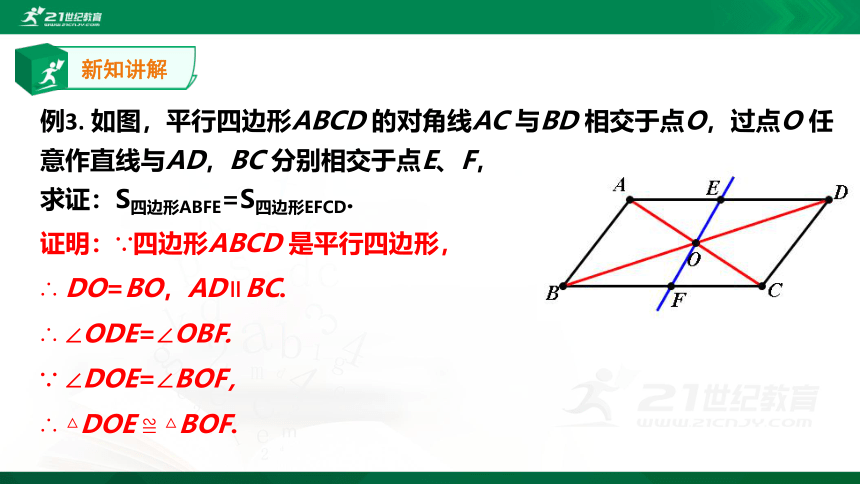
例3. 如图,平行四边形ABCD 的对角线AC 与BD 相交于点O,过点O 任意作直线与AD,BC 分别相交于点E、F,
求证:S四边形ABFE=S四边形EFCD.
证明:∵四边形ABCD 是平行四边形,
∴ DO=BO,AD∥BC.
∴ ∠ODE=∠OBF.
∵ ∠DOE=∠BOF,
∴ △DOE ≌ △BOF.
新知讲解
∴S四边形ABFE=S四边形EFCD.
课堂练习
1.如图,在□ABCD 中,AC,BD 相交于点O.
已知:AC=24cm,BD=38cm,AD=28cm.
则△OBC的周长为( )cm.
2.在□ABCD 中,AC=24,BD=38,AB=m,
则m 的取值范围是( )
A. 24C.7
59
C
课堂练习
3.如图, □ ABCD 的两条对角线AC、BD相交于点O,过点O的直线与AD、BC 分别相交于点E、F,已知□ ABCD 的面积是12cm2,则图中阴影部分的面积是 .。
6cm2
课堂练习
4.如图,四边形ABCD 是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA 的长.
解:∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
又∵AC⊥BC,
∴△ABC 是直角三角形.
又∵OA=OC,
课堂练习
5. 如图,平行四边形ABCD 的对角线AC、BD 相交于点O,E,F 分别是OA,OC 的中点,连接BE,DF.
求证:△DOF ≌ △BOE.
证明:∵四边形ABCD 是平行四边形,
∴OB=OD,OA=OC.
∵E,F 分别是OA,OC 的中点,
又∵ ∠DOF= ∠BOE
∴△DOF ≌ △BOE.
拓展提高
6.如图,在□ ABCD 中,对角线AC、BD相交于点O,E、F是对角线AC上两点,DF=BE,DF‖BE,
求证:AE=CF,
证明:∵DF‖BE
∴∠ODF= ∠OBE,∠DFO= ∠BEO
又∵DF=BE,
∴△DOF ≌ △BOE.
∴OE=OF,
又∵OA=OC ∴AE=CF,
中考链接
7.(2019·镇江)在□ ABCD 中,两条对角线AC、BD相交于点O,若AC=10,BD=8,下列结论正确的是( )
A. OA=5,OB=3 B. OA=6,OC=4
C. OA=5,OB=4 D.OA=5,OC=4
8.(2019·南通)平行四边形一边长为12cm,那么它的两条对角线的长度可能是( )
A.8cm和14cm B.10cm和14cm
C.18cm和20cm D.10cm和24
C
C
课堂总结
本节课你有什么收获?
一、平行四边形性质3:
平行四边形对角线互相平分.
二、过平行四边形对角线交点的任意一条直线,均等分平行四边形的面积.
板书设计
19.2 平行四边形的性质(2)
1.平行四边形的性质(2)
2.过平行四边形对角线交点的任意一条直线,均等分平行四边形的面积.
作业布置
课本
P79 练习题第1和第2题
P84 第5题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第2课时 平行四边形对角线性质
沪科版 八年级下
19.2 平行四边形
新知导入
一、复习提问:
问题1.请叙述平行四边形的性质1?
平行四边形的性质1:平行四边形的对边相等.
问题2.请叙述平行四边形的性质2?
平行四边形的性质2:平行四边形的对角相等.
问题3.请问平行四边形还有什么性质呢?
新知讲解
新知讲解
同学们,由此你们能得到平行四边形什么性质呢?
新知讲解
三、归纳小结:
平行四边形性质3:
平行四边形对角线互相平分.
应用格式:
∵□ABCD 的对角线AC、BD 相交于点O.
∴OA=OC,OB=OD.
新知讲解
四、例题剖析
例1.在□ABCD 中,AC 与BD 交于点O,OA=12cm,
OB=19cm,则AC = cm, BD = cm.
解:∵四边形ABCD是平行四边形,
∴OA=OC=12cm,OB=OD=19cm.
∴AC=2OA=2×12=24cm
BD=2OB=2×19=38cm
24
38
新知讲解
例2.如图,平行四边形ABCD 中,对角线AC、BD相交于点O,AB⊥AC,AB=3,AD=5,求BD的长.
解:∵四边形ABCD是平行四边形,
∴BC=AD=5,
∵AB⊥AC,∴△ABC是直角三角形.
新知讲解
例3. 如图,平行四边形ABCD 的对角线AC 与BD 相交于点O,过点O 任意作直线与AD,BC 分别相交于点E、F,
求证:S四边形ABFE=S四边形EFCD.
证明:∵四边形ABCD 是平行四边形,
∴ DO=BO,AD∥BC.
∴ ∠ODE=∠OBF.
∵ ∠DOE=∠BOF,
∴ △DOE ≌ △BOF.
新知讲解
∴S四边形ABFE=S四边形EFCD.
课堂练习
1.如图,在□ABCD 中,AC,BD 相交于点O.
已知:AC=24cm,BD=38cm,AD=28cm.
则△OBC的周长为( )cm.
2.在□ABCD 中,AC=24,BD=38,AB=m,
则m 的取值范围是( )
A. 24
59
C
课堂练习
3.如图, □ ABCD 的两条对角线AC、BD相交于点O,过点O的直线与AD、BC 分别相交于点E、F,已知□ ABCD 的面积是12cm2,则图中阴影部分的面积是 .。
6cm2
课堂练习
4.如图,四边形ABCD 是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA 的长.
解:∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
又∵AC⊥BC,
∴△ABC 是直角三角形.
又∵OA=OC,
课堂练习
5. 如图,平行四边形ABCD 的对角线AC、BD 相交于点O,E,F 分别是OA,OC 的中点,连接BE,DF.
求证:△DOF ≌ △BOE.
证明:∵四边形ABCD 是平行四边形,
∴OB=OD,OA=OC.
∵E,F 分别是OA,OC 的中点,
又∵ ∠DOF= ∠BOE
∴△DOF ≌ △BOE.
拓展提高
6.如图,在□ ABCD 中,对角线AC、BD相交于点O,E、F是对角线AC上两点,DF=BE,DF‖BE,
求证:AE=CF,
证明:∵DF‖BE
∴∠ODF= ∠OBE,∠DFO= ∠BEO
又∵DF=BE,
∴△DOF ≌ △BOE.
∴OE=OF,
又∵OA=OC ∴AE=CF,
中考链接
7.(2019·镇江)在□ ABCD 中,两条对角线AC、BD相交于点O,若AC=10,BD=8,下列结论正确的是( )
A. OA=5,OB=3 B. OA=6,OC=4
C. OA=5,OB=4 D.OA=5,OC=4
8.(2019·南通)平行四边形一边长为12cm,那么它的两条对角线的长度可能是( )
A.8cm和14cm B.10cm和14cm
C.18cm和20cm D.10cm和24
C
C
课堂总结
本节课你有什么收获?
一、平行四边形性质3:
平行四边形对角线互相平分.
二、过平行四边形对角线交点的任意一条直线,均等分平行四边形的面积.
板书设计
19.2 平行四边形的性质(2)
1.平行四边形的性质(2)
2.过平行四边形对角线交点的任意一条直线,均等分平行四边形的面积.
作业布置
课本
P79 练习题第1和第2题
P84 第5题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
