北师大版数学八年级下册3.3中心对称学案(无答案)
文档属性
| 名称 | 北师大版数学八年级下册3.3中心对称学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 365.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:37:55 | ||
图片预览

文档简介
2020年春季学期延期初中数学 “空中课堂”
学习经历案
一、目标引领
课题名称:北师大版 八年级 下册 数学 第三章 3.3中心对称
达成目标: (1)观察 :了解中心对称的概念(抽象美) (2)操作:探索中心对称的性质(探索美) (3)欣赏:认识自然界和现实生活中的中心对称图形(欣赏美) (4)设计:积累数学活动经验,增强动手实践能力,发展空间观念(创造美)
课前准备建议: 复习七年级下册《轴对称》 复习上节课知识《图形的旋转》
二、学习指导
录像课 学习经历案
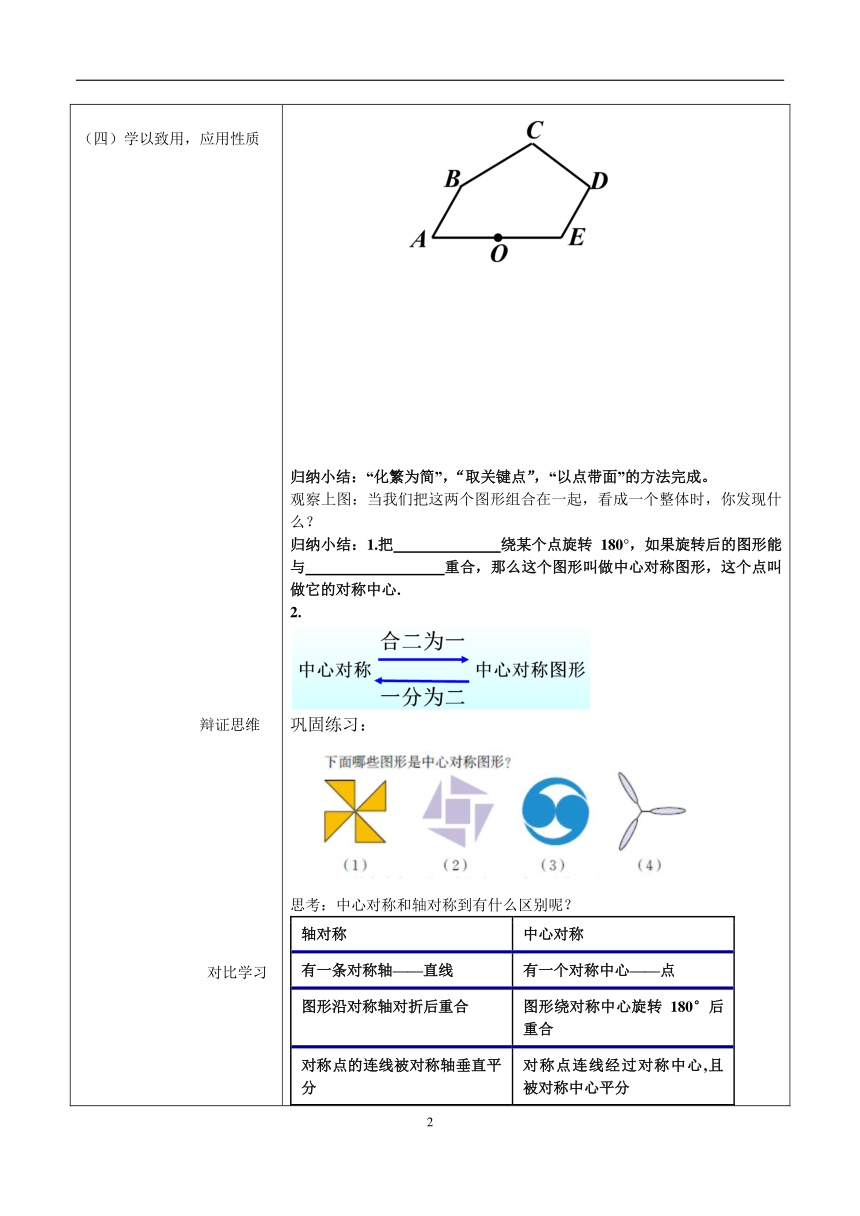
(一)创设情境,导入新课 (二)对比发现,提炼概念 (三)动手操作,探索性质 “上天给人一份困难的同时也给人一份智慧。——雨果”愿你在今后的学习与生活中做一名积极克服困难的智者! (四)学以致用,应用性质 辩证思维 对比学习 (五)盘点收获,课堂小结 数字小游戏:这里有一串数字68690137,电子码形式呈现,将其中的三个数字旋转180°,结果不变,你能告诉我是哪三个数字吗? 大家请看这两个图形能否沿着某条直线折叠而重合 如果不能,那图(1)经过怎样的运动变化可以与图(2)重合? 那么我们把经过这种运动变化而重合的图形之间的关系就称为为“ ”,课本81页找到这个定义,重点标注下来。 归纳小结: 如果把一个图形 ,能够与另一个图形重合,那么就说这两个图 或 ,这个点叫做它们的 . 自己画一个图形,选取一个旋转中心,把所画的图形绕旋转中心旋转180°,连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试. 归纳小结:中心对称的性质:成中心对称的两个图形中,对应点所连线段 ,且 . 例:如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形. 归纳小结:“化繁为简”,“取关键点”,“以点带面”的方法完成。 观察上图:当我们把这两个图形组合在一起,看成一个整体时,你发现什么? 归纳小结:1.把 绕某个点旋转180°,如果旋转后的图形能与 重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心. 2. 巩固练习: 思考:中心对称和轴对称到有什么区别呢? 轴对称中心对称有一条对称轴——直线有一个对称中心——点图形沿对称轴对折后重合图形绕对称中心旋转180°后重合对称点的连线被对称轴垂直平分对称点连线经过对称中心,且被对称中心平分
轻松一刻: 魔术师把5张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某两张牌旋转180°. 魔术师解除蒙具后,看到扑克牌如下图: 魔术师很快确定了哪两张牌被旋转过,你知道是哪两张吗? 通过本节课的学习,你在知识与技能、过程与方法、情感态度与价值观等方面有哪些收获?
三、当堂检测
1.下面有4个汽车标致图案,其中是中心对称图形的是( ) A.②③④ B.③④ C.④ D.② 2.下列图形中,是轴对称图形,但不是中心对称图形的是( ) A. B. C. D. 3.如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABC成中心对称的三角形.
作业布置
一、必做作业: 1.下列四张扑克牌图案,属于中心对称图形的是( ) A. B. C. D. 2.下列四个图形中,既是轴对称图形又是中心对称图形的是( ) A. B. C. D. 3.下列图形中是中心对称图形,而不是轴对称图形的是( ) A.等边三角形 B.平行四边形 C.矩形 D.菱形 4.在平行四边形、菱形、矩形、正方形、圆中,既是中心对称图形又是轴对称图形的图形个数为( ) A.1 B.2 C.3 D.4 5.菱形、矩形、正方形既是中心对称图形,又是轴对称图形,它们的对称中心只有一个,而对称轴的个数依次是( ) A.1,1,1 B.2,2,2 C.2,2,4 D.4,2,4 6.如图,线段AB、CD互相平分于点O,过O作EF交AC于E, 交BD于F,则这个图形是中心对称图形,对称中心是O.指出图 形中的对应点_____ __,对应线段____ ___, 对应三角形____ ___. 7.中心对称图形的对应点连线经过__ _____,并且被___ ____平分. 8.已知六边形ABCDEF是以O为中心的中心对称图形(如图),画出六边形ABCDEF的全部图形,并指出所有的对应点和对应线段. 二.选做作业: 9. 如图,正△ABC与正△A1B1C1关于某点中心对称,已知A,A1,B三点的坐标分别是(0,4),(0,3),(0,2). (1)求对称中心的坐标; (2)写出顶点C,C1的坐标.
五、总结反思(学生填写)
六、错题纠正(学生填写)
1
学习经历案
一、目标引领
课题名称:北师大版 八年级 下册 数学 第三章 3.3中心对称
达成目标: (1)观察 :了解中心对称的概念(抽象美) (2)操作:探索中心对称的性质(探索美) (3)欣赏:认识自然界和现实生活中的中心对称图形(欣赏美) (4)设计:积累数学活动经验,增强动手实践能力,发展空间观念(创造美)
课前准备建议: 复习七年级下册《轴对称》 复习上节课知识《图形的旋转》
二、学习指导
录像课 学习经历案
(一)创设情境,导入新课 (二)对比发现,提炼概念 (三)动手操作,探索性质 “上天给人一份困难的同时也给人一份智慧。——雨果”愿你在今后的学习与生活中做一名积极克服困难的智者! (四)学以致用,应用性质 辩证思维 对比学习 (五)盘点收获,课堂小结 数字小游戏:这里有一串数字68690137,电子码形式呈现,将其中的三个数字旋转180°,结果不变,你能告诉我是哪三个数字吗? 大家请看这两个图形能否沿着某条直线折叠而重合 如果不能,那图(1)经过怎样的运动变化可以与图(2)重合? 那么我们把经过这种运动变化而重合的图形之间的关系就称为为“ ”,课本81页找到这个定义,重点标注下来。 归纳小结: 如果把一个图形 ,能够与另一个图形重合,那么就说这两个图 或 ,这个点叫做它们的 . 自己画一个图形,选取一个旋转中心,把所画的图形绕旋转中心旋转180°,连接旋转前后一组对应点,你发现了什么?再选几组对应点试一试. 归纳小结:中心对称的性质:成中心对称的两个图形中,对应点所连线段 ,且 . 例:如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形. 归纳小结:“化繁为简”,“取关键点”,“以点带面”的方法完成。 观察上图:当我们把这两个图形组合在一起,看成一个整体时,你发现什么? 归纳小结:1.把 绕某个点旋转180°,如果旋转后的图形能与 重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心. 2. 巩固练习: 思考:中心对称和轴对称到有什么区别呢? 轴对称中心对称有一条对称轴——直线有一个对称中心——点图形沿对称轴对折后重合图形绕对称中心旋转180°后重合对称点的连线被对称轴垂直平分对称点连线经过对称中心,且被对称中心平分
轻松一刻: 魔术师把5张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某两张牌旋转180°. 魔术师解除蒙具后,看到扑克牌如下图: 魔术师很快确定了哪两张牌被旋转过,你知道是哪两张吗? 通过本节课的学习,你在知识与技能、过程与方法、情感态度与价值观等方面有哪些收获?
三、当堂检测
1.下面有4个汽车标致图案,其中是中心对称图形的是( ) A.②③④ B.③④ C.④ D.② 2.下列图形中,是轴对称图形,但不是中心对称图形的是( ) A. B. C. D. 3.如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABC成中心对称的三角形.
作业布置
一、必做作业: 1.下列四张扑克牌图案,属于中心对称图形的是( ) A. B. C. D. 2.下列四个图形中,既是轴对称图形又是中心对称图形的是( ) A. B. C. D. 3.下列图形中是中心对称图形,而不是轴对称图形的是( ) A.等边三角形 B.平行四边形 C.矩形 D.菱形 4.在平行四边形、菱形、矩形、正方形、圆中,既是中心对称图形又是轴对称图形的图形个数为( ) A.1 B.2 C.3 D.4 5.菱形、矩形、正方形既是中心对称图形,又是轴对称图形,它们的对称中心只有一个,而对称轴的个数依次是( ) A.1,1,1 B.2,2,2 C.2,2,4 D.4,2,4 6.如图,线段AB、CD互相平分于点O,过O作EF交AC于E, 交BD于F,则这个图形是中心对称图形,对称中心是O.指出图 形中的对应点_____ __,对应线段____ ___, 对应三角形____ ___. 7.中心对称图形的对应点连线经过__ _____,并且被___ ____平分. 8.已知六边形ABCDEF是以O为中心的中心对称图形(如图),画出六边形ABCDEF的全部图形,并指出所有的对应点和对应线段. 二.选做作业: 9. 如图,正△ABC与正△A1B1C1关于某点中心对称,已知A,A1,B三点的坐标分别是(0,4),(0,3),(0,2). (1)求对称中心的坐标; (2)写出顶点C,C1的坐标.
五、总结反思(学生填写)
六、错题纠正(学生填写)
1
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
