五年级下册数学课件-《信息窗一(比例的意义)》 青岛五四学制版 (共21张PPT)
文档属性
| 名称 | 五年级下册数学课件-《信息窗一(比例的意义)》 青岛五四学制版 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 07:00:44 | ||
图片预览



文档简介
(共21张PPT)
五 啤酒生产中的数学
复习补偿
1.什么叫做 “比”?举例说明比的各部分名称。
2.“比”的基本性质是什么?
两数相除又叫两个数的比。
比的前项与后项都乘以或除以同一个不是0的数,
比值不变。
如3 :2 ,其中3是比的前项,2是比的后项,
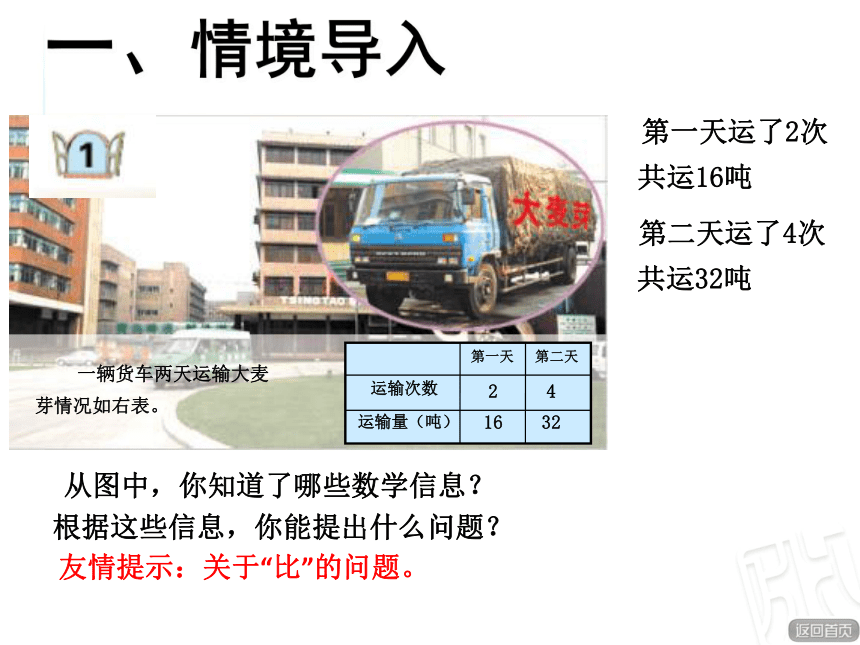
啤酒生产的主要原料——大麦芽
从图中,你知道了哪些数学信息?
运动会报名
男生志愿者
王东 李明 刘刚
李亮 丁一 张帅
于军 刘平 赵海
女生志愿者
李燕 王静 牛莉
方悦 于美 张红
孙娟
第一天运了2次
共运16吨
共运32吨
一、情境导入
根据这些信息,你能提出什么问题?
一辆货车两天运输大麦
芽情况如右表。
运输次数
运输量(吨)
第一天
第二天
2 4
16 32
第二天运了4次
友情提示:关于“比”的问题。
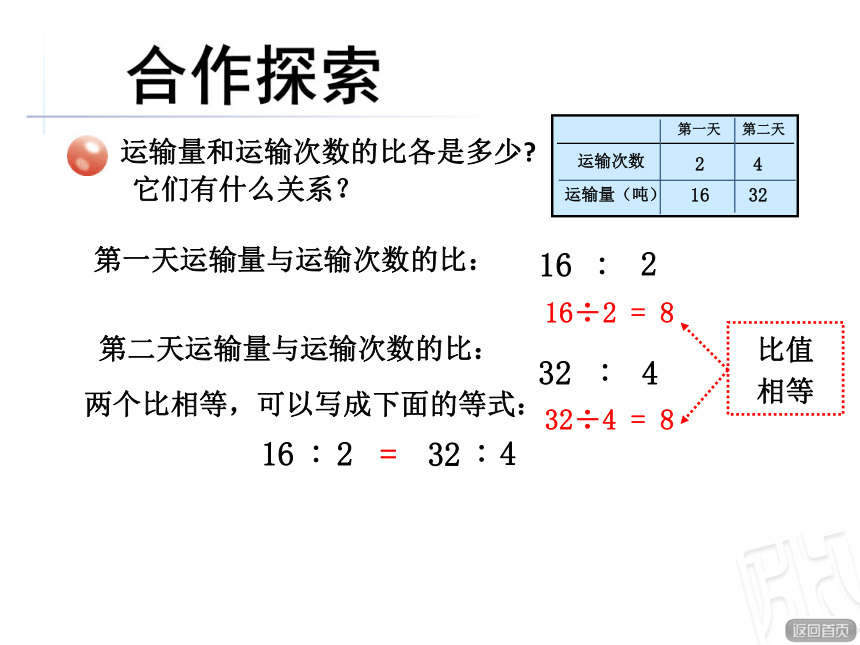
合作探索
运输量和运输次数的比各是多少?
16
2
32
4
:
第一天运输量与运输次数的比:
它们有什么关系?
第二天运输量与运输次数的比:
:
16÷2 = 8
32÷4 = 8
比值
相等
16
2
32
4
:
:
=
两个比相等,可以写成下面的等式:
运输次数
运输量(吨)
第一天
第二天
2 4
16 32
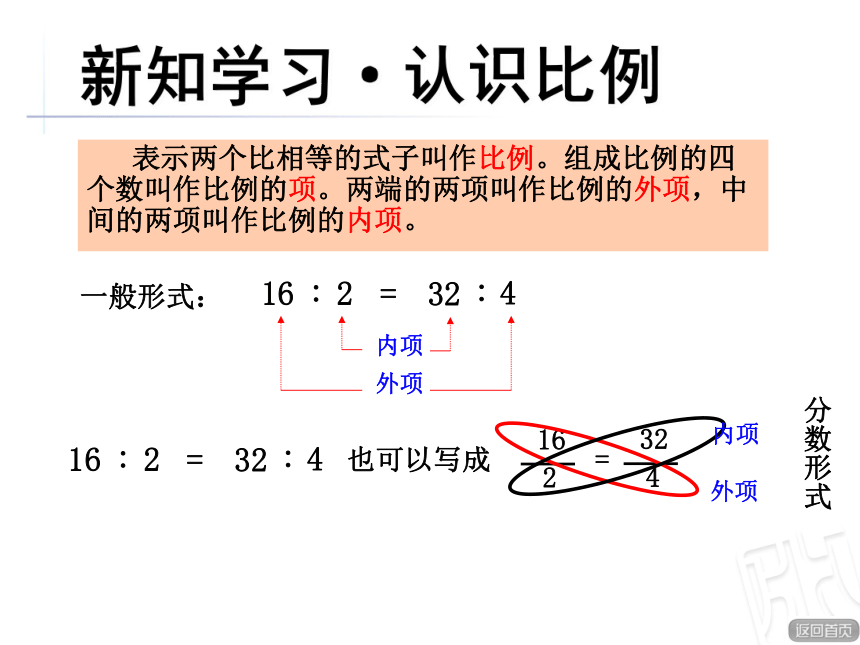
新知学习·认识比例
表示两个比相等的式子叫作比例。组成比例的四个数叫作比例的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。
16
2
32
4
:
:
=
内项
外项
也可以写成
16
2
32
4
16
2
32
4
:
:
=
=
内项
外项
一般形式:
分数形式
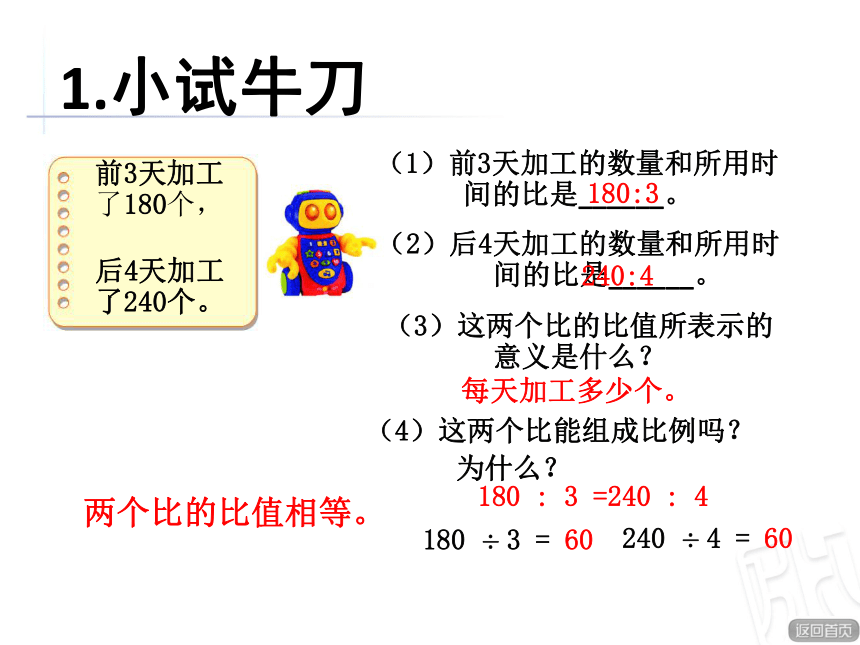
1.小试牛刀
(2)后4天加工的数量和所用时
间的比是______。
(1)前3天加工的数量和所用时
间的比是______。
(4)这两个比能组成比例吗?
为什么?
180:3
240:4
180 : 3 =240 : 4
180 ÷ 3 = 60
240 ÷ 4 = 60
后4天加工
了240个。
前3天加工
了180个,
(3)这两个比的比值所表示的
意义是什么?
每天加工多少个。
两个比的比值相等。
80:4
20:10
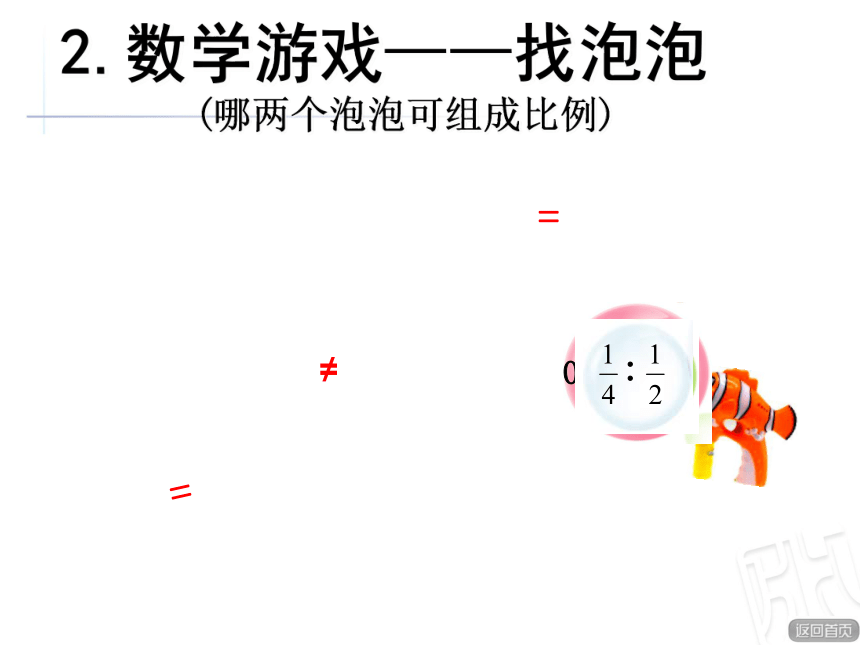
2.数学游戏——找泡泡
(哪两个泡泡可组成比例)
0.6:0.03
18:12
15:10
=
:
=
≠
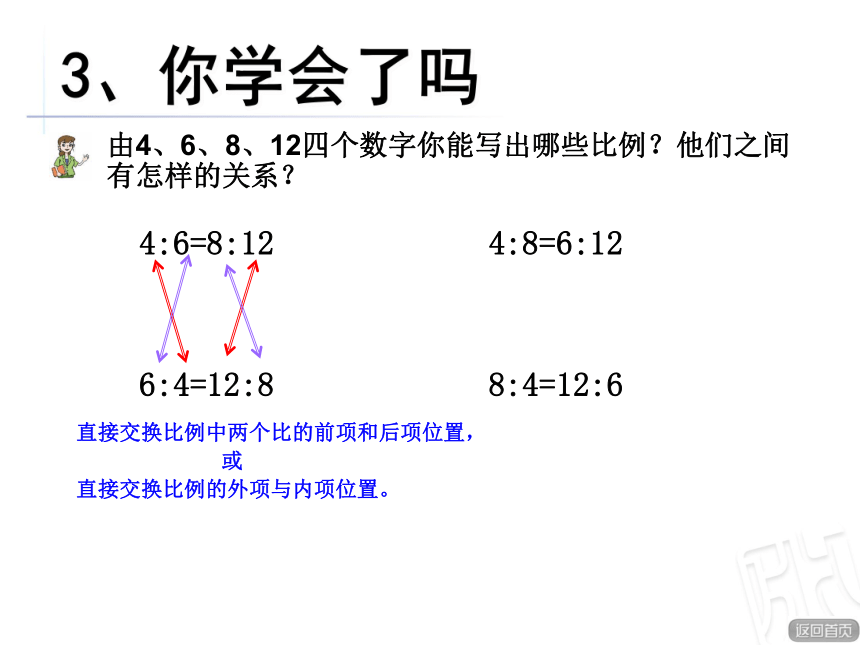
3、你学会了吗
4:6=8:12
4:8=6:12
6:4=12:8
8:4=12:6
由4、6、8、12四个数字你能写出哪些比例?他们之间有怎样的关系?
直接交换比例中两个比的前项和后项位置,
或
直接交换比例的外项与内项位置。
合作探索(小组交流)
和
差
积
商
在比例里,两个外项与两个内项之间有什么关系呢?
我们以“4:6=8:12”为例来研究:
提示: 分别算出两个外项和两个内项的和、差、积、商,看看从中能发现什么规律?
继续
你能根据观察试着先猜想下吗?
合作探索
两个外项的和与两个内项的和:
两个外项的和:4 + 12 = 16
两个内项的和:6 + 8 = 14
两个外项的和与两个内项的和之间没有发现规律。
4 : 6 = 8 : 12
返回
合作探索
两个外项的差与两个内项的差:
两个外项的差:12 - 4 = 8
两个内项的差:8 - 6 = 2
4 : 6 = 8 : 12
返回
两个外项的差与两个内项的差之间没有发现规律。
合作探索
两个外项的积与两个内项的积:
两个外项的积:4 × 12 = 48
两个内项的积:6 ×8 = 48
4 : 6 = 8 : 12
返回
两个外项的积等于两个内项的积。
两个外项的商与两个内项的商:
两个外项的商:12 ÷ 4 = 3
两个内项的商:8÷ 6 =
4 : 6 = 8 : 12
返回
两个外项的商与两个内项的商之间没有发现规律。
合作探索
回顾刚才的研究,可以得出一个什么结论?
在比例里,两个外项的积等于两个内项的积。
这是不是一个规律呢?大家再举一例来验证一下,
是不任何比例式都有这样的规律。
合作探索
两个内项的积:4 ×100 = 400
两个外项的积:80 × 5 = 400
=
40 : 2 = 60 : 3
两个内项的积:2 × 60 = 120
两个外项的积:40 × 3 = 120
举例验证:
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
新知学习·比例的基本性质
现在我们可以确信:
提醒:注意与比的基本性质的区别。
新知学习·比例的基本性质
你能回顾下刚才我们归纳出比例基本性质的
探究过程的吗?
先观察猜想结论;
第二,
第三,
第四,
这是我们小学阶段探究数学问题经常用的
思维过程和方法!
第一,
通过举例计算探究初步得出结论;
再重新举例验证结论;
总结归纳出比例的基本性质。
学以致用
你能求出下面比例中的未知项吗?
20 : 25 = 4 : χ
解: 20χ= 25 × 4
20χ= 100
χ= 5
求比例中的未知项,叫作解比例。
比例的基本性质:
在比例里,两个外项的积等于两个内项的积。
25 : 20 = χ : 4
解: 20χ= 25 × 4
20χ= 100
χ= 5
思路:根据比例的基本性质把比例式“转化”为方程
课堂小结
同学们,这节课,你都有哪些收获?
一、你学到了什么知识?
什么是“比例”,内项、外项名称,两种形式——
一般形式与分数形式。
比例的基本性质。
“比例”与“比”有什么关系;比例的简单变形规律。
与“比”的基本性质区别。
解比例。
1.
2.
3.
先观察猜想结论;
第二,
第三,
第四,
第一,
通过举例计算探究初步得出结论;
再重新举例验证结论;
总结归纳出比例的基本性质。
课堂小结
二.用到什么样的思想方法
(一)发现总结规律的方法——合情推理:
(二)解决新知问题的方法:
解比例是根据比例的基本性质把比例式
“转化”为方程。
思维提升:
你会把下面的等式改写成比例吗?
5×6=3×10
提示:怎样根据比例的基本性质来解决这个问题呢?
如果把这个等式看成是原来的比例变形得到,
那式中的5和6应当是什么?3和10呢?
也就是要“逆向”思考问题!
即填空:( ):( )=( ):( )
5
6
3
10
3
10
5
6
五 啤酒生产中的数学
复习补偿
1.什么叫做 “比”?举例说明比的各部分名称。
2.“比”的基本性质是什么?
两数相除又叫两个数的比。
比的前项与后项都乘以或除以同一个不是0的数,
比值不变。
如3 :2 ,其中3是比的前项,2是比的后项,
啤酒生产的主要原料——大麦芽
从图中,你知道了哪些数学信息?
运动会报名
男生志愿者
王东 李明 刘刚
李亮 丁一 张帅
于军 刘平 赵海
女生志愿者
李燕 王静 牛莉
方悦 于美 张红
孙娟
第一天运了2次
共运16吨
共运32吨
一、情境导入
根据这些信息,你能提出什么问题?
一辆货车两天运输大麦
芽情况如右表。
运输次数
运输量(吨)
第一天
第二天
2 4
16 32
第二天运了4次
友情提示:关于“比”的问题。
合作探索
运输量和运输次数的比各是多少?
16
2
32
4
:
第一天运输量与运输次数的比:
它们有什么关系?
第二天运输量与运输次数的比:
:
16÷2 = 8
32÷4 = 8
比值
相等
16
2
32
4
:
:
=
两个比相等,可以写成下面的等式:
运输次数
运输量(吨)
第一天
第二天
2 4
16 32
新知学习·认识比例
表示两个比相等的式子叫作比例。组成比例的四个数叫作比例的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。
16
2
32
4
:
:
=
内项
外项
也可以写成
16
2
32
4
16
2
32
4
:
:
=
=
内项
外项
一般形式:
分数形式
1.小试牛刀
(2)后4天加工的数量和所用时
间的比是______。
(1)前3天加工的数量和所用时
间的比是______。
(4)这两个比能组成比例吗?
为什么?
180:3
240:4
180 : 3 =240 : 4
180 ÷ 3 = 60
240 ÷ 4 = 60
后4天加工
了240个。
前3天加工
了180个,
(3)这两个比的比值所表示的
意义是什么?
每天加工多少个。
两个比的比值相等。
80:4
20:10
2.数学游戏——找泡泡
(哪两个泡泡可组成比例)
0.6:0.03
18:12
15:10
=
:
=
≠
3、你学会了吗
4:6=8:12
4:8=6:12
6:4=12:8
8:4=12:6
由4、6、8、12四个数字你能写出哪些比例?他们之间有怎样的关系?
直接交换比例中两个比的前项和后项位置,
或
直接交换比例的外项与内项位置。
合作探索(小组交流)
和
差
积
商
在比例里,两个外项与两个内项之间有什么关系呢?
我们以“4:6=8:12”为例来研究:
提示: 分别算出两个外项和两个内项的和、差、积、商,看看从中能发现什么规律?
继续
你能根据观察试着先猜想下吗?
合作探索
两个外项的和与两个内项的和:
两个外项的和:4 + 12 = 16
两个内项的和:6 + 8 = 14
两个外项的和与两个内项的和之间没有发现规律。
4 : 6 = 8 : 12
返回
合作探索
两个外项的差与两个内项的差:
两个外项的差:12 - 4 = 8
两个内项的差:8 - 6 = 2
4 : 6 = 8 : 12
返回
两个外项的差与两个内项的差之间没有发现规律。
合作探索
两个外项的积与两个内项的积:
两个外项的积:4 × 12 = 48
两个内项的积:6 ×8 = 48
4 : 6 = 8 : 12
返回
两个外项的积等于两个内项的积。
两个外项的商与两个内项的商:
两个外项的商:12 ÷ 4 = 3
两个内项的商:8÷ 6 =
4 : 6 = 8 : 12
返回
两个外项的商与两个内项的商之间没有发现规律。
合作探索
回顾刚才的研究,可以得出一个什么结论?
在比例里,两个外项的积等于两个内项的积。
这是不是一个规律呢?大家再举一例来验证一下,
是不任何比例式都有这样的规律。
合作探索
两个内项的积:4 ×100 = 400
两个外项的积:80 × 5 = 400
=
40 : 2 = 60 : 3
两个内项的积:2 × 60 = 120
两个外项的积:40 × 3 = 120
举例验证:
在比例里,两个外项的积等于两个内项的积,这叫作比例的基本性质。
新知学习·比例的基本性质
现在我们可以确信:
提醒:注意与比的基本性质的区别。
新知学习·比例的基本性质
你能回顾下刚才我们归纳出比例基本性质的
探究过程的吗?
先观察猜想结论;
第二,
第三,
第四,
这是我们小学阶段探究数学问题经常用的
思维过程和方法!
第一,
通过举例计算探究初步得出结论;
再重新举例验证结论;
总结归纳出比例的基本性质。
学以致用
你能求出下面比例中的未知项吗?
20 : 25 = 4 : χ
解: 20χ= 25 × 4
20χ= 100
χ= 5
求比例中的未知项,叫作解比例。
比例的基本性质:
在比例里,两个外项的积等于两个内项的积。
25 : 20 = χ : 4
解: 20χ= 25 × 4
20χ= 100
χ= 5
思路:根据比例的基本性质把比例式“转化”为方程
课堂小结
同学们,这节课,你都有哪些收获?
一、你学到了什么知识?
什么是“比例”,内项、外项名称,两种形式——
一般形式与分数形式。
比例的基本性质。
“比例”与“比”有什么关系;比例的简单变形规律。
与“比”的基本性质区别。
解比例。
1.
2.
3.
先观察猜想结论;
第二,
第三,
第四,
第一,
通过举例计算探究初步得出结论;
再重新举例验证结论;
总结归纳出比例的基本性质。
课堂小结
二.用到什么样的思想方法
(一)发现总结规律的方法——合情推理:
(二)解决新知问题的方法:
解比例是根据比例的基本性质把比例式
“转化”为方程。
思维提升:
你会把下面的等式改写成比例吗?
5×6=3×10
提示:怎样根据比例的基本性质来解决这个问题呢?
如果把这个等式看成是原来的比例变形得到,
那式中的5和6应当是什么?3和10呢?
也就是要“逆向”思考问题!
即填空:( ):( )=( ):( )
5
6
3
10
3
10
5
6
