五年级下册数学课件6.5 总复习:图形与几何(平面图形的周长和面积)沪教版 (共16张PPT)
文档属性
| 名称 | 五年级下册数学课件6.5 总复习:图形与几何(平面图形的周长和面积)沪教版 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 143.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 08:29:57 | ||
图片预览


文档简介
(共16张PPT)
立体图形的表面积和体积复习
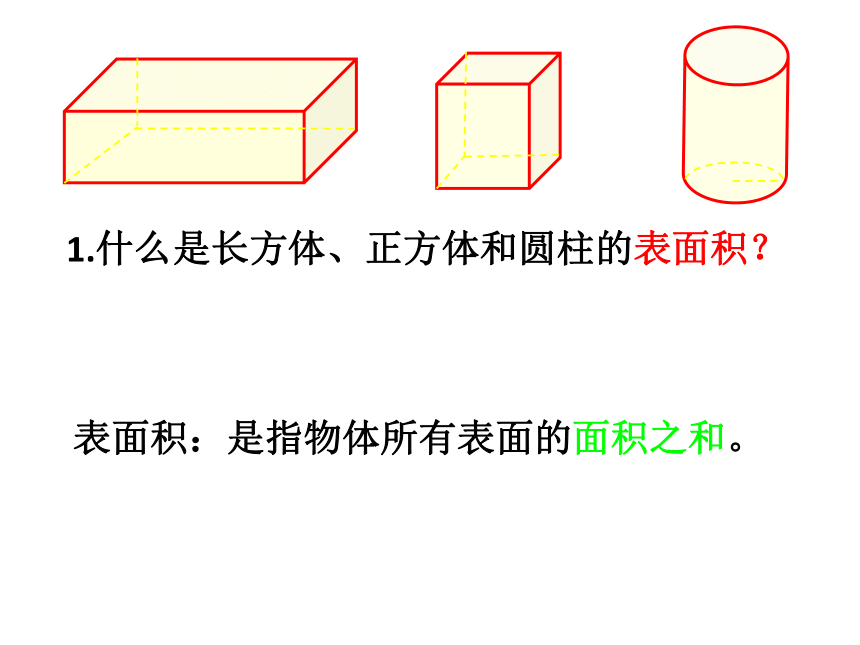
1.什么是长方体、正方体和圆柱的表面积?
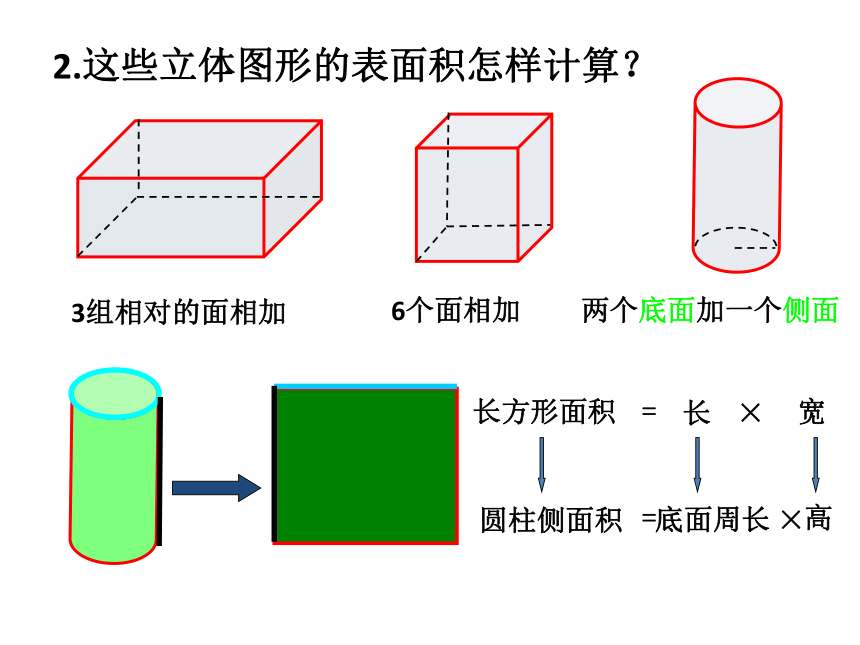
2.这些立体图形的表面积怎样计算?
3.计算表面积时有什么要注意的问题?
1.什么是长方体、正方体和圆柱的表面积?
表面积:是指物体所有表面的面积之和。
2.这些立体图形的表面积怎样计算?
3组相对的面相加
6个面相加
两个底面加一个侧面
底面周长
×
=
宽
长方形面积
×
长
=
圆柱侧面积
高
3. 计算表面积时要注意什么问题?
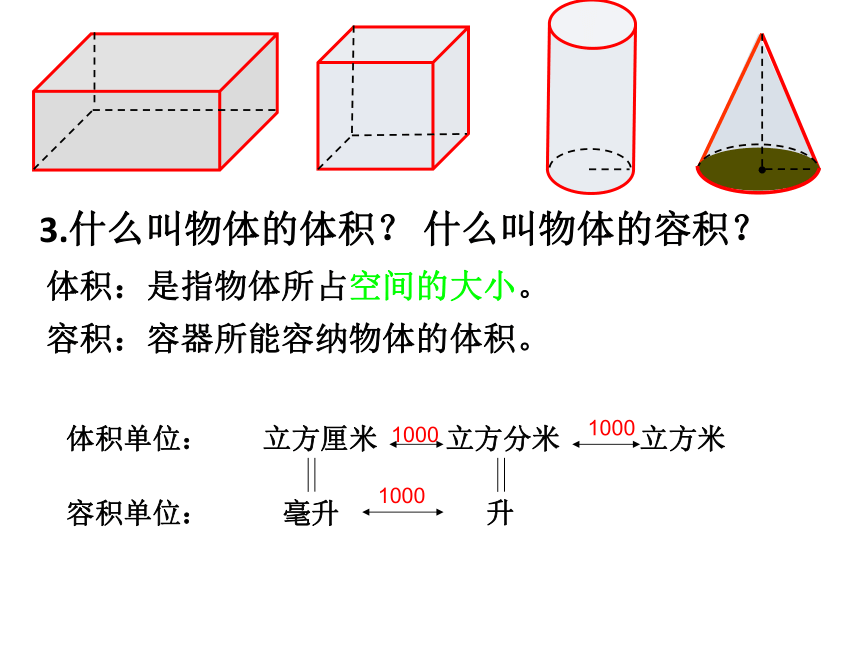
3.什么叫物体的体积? 什么叫物体的容积?
体积:是指物体所占空间的大小。
立方厘米
立方分米
立方米
容积:容器所能容纳物体的体积。
毫升
升
体积单位:
容积单位:
1000
1000
1000
特殊的长方体
是与它等底等高的圆柱的三分之一
4.这些立体图形的体积公式分别是怎样得到的?
a
a
b
h
a
a
s
s
h
h
1.在括号里填上合适的单位名称:
(1)一间卧室的地面面积是15( )
(2)一瓶牛奶大约有250( )
(3)我们教室的空间大约是144( )
平方米
毫升
立方米
2.求下列各立体图形的表面积:(只列式不计算)
(1)棱长4厘米的正方体。
(2)长5厘米、宽4厘米
(3)底面半径1分米
4×4×6
5×4×2+ 5×3×2 +3×4×2
(5×4+ 5×3+3×4)×2
∏ ×12×2
+ ∏ ×2×5
、高3厘米的长方体。
,高5分米的圆柱。
回答下面的问题,并列出算式(不计算):
1.一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2× ∏ ×10
∏ ×102
∏ ×102+2×∏×10×20
∏ ×102×20
基本练习:
2.做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3.做一个圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4.做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?
18.84 × 4
∏ ×32×2 + 2× ∏ ×3×4
∏ ×(6÷2)2 + ∏ ×6×4
基本练习:
1.把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米?
20÷4=5(平方厘米)
30×5=150(平方厘米)
答:这根木材原来的体积是150平方厘米。
拓展练习:
2.将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米?
拓展练习:
3.计算下面半圆柱的表面积和体积。
10cm
5cm
敬请指导!
立体图形的表面积和体积复习
1.什么是长方体、正方体和圆柱的表面积?
2.这些立体图形的表面积怎样计算?
3.计算表面积时有什么要注意的问题?
1.什么是长方体、正方体和圆柱的表面积?
表面积:是指物体所有表面的面积之和。
2.这些立体图形的表面积怎样计算?
3组相对的面相加
6个面相加
两个底面加一个侧面
底面周长
×
=
宽
长方形面积
×
长
=
圆柱侧面积
高
3. 计算表面积时要注意什么问题?
3.什么叫物体的体积? 什么叫物体的容积?
体积:是指物体所占空间的大小。
立方厘米
立方分米
立方米
容积:容器所能容纳物体的体积。
毫升
升
体积单位:
容积单位:
1000
1000
1000
特殊的长方体
是与它等底等高的圆柱的三分之一
4.这些立体图形的体积公式分别是怎样得到的?
a
a
b
h
a
a
s
s
h
h
1.在括号里填上合适的单位名称:
(1)一间卧室的地面面积是15( )
(2)一瓶牛奶大约有250( )
(3)我们教室的空间大约是144( )
平方米
毫升
立方米
2.求下列各立体图形的表面积:(只列式不计算)
(1)棱长4厘米的正方体。
(2)长5厘米、宽4厘米
(3)底面半径1分米
4×4×6
5×4×2+ 5×3×2 +3×4×2
(5×4+ 5×3+3×4)×2
∏ ×12×2
+ ∏ ×2×5
、高3厘米的长方体。
,高5分米的圆柱。
回答下面的问题,并列出算式(不计算):
1.一个圆柱形无盖的水桶,底面半径10分米,高20分米。
(1)给这个水桶加个箍,是求什么?
(2)求这个水桶的占地面积,是求什么?
(3)做这样一个水桶用多少铁皮,是求什么?
(4)这个水桶能装多少水,是求什么?
2× ∏ ×10
∏ ×102
∏ ×102+2×∏×10×20
∏ ×102×20
基本练习:
2.做一个圆柱形的油箱,底面半径3分米,高4分米。至少需要铁皮多少平方分米?
3.做一个圆柱形的水桶,底面直径6分米,高4分米。至少需要铁皮多少平方分米?
4.做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?
18.84 × 4
∏ ×32×2 + 2× ∏ ×3×4
∏ ×(6÷2)2 + ∏ ×6×4
基本练习:
1.把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米?
20÷4=5(平方厘米)
30×5=150(平方厘米)
答:这根木材原来的体积是150平方厘米。
拓展练习:
2.将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米?
拓展练习:
3.计算下面半圆柱的表面积和体积。
10cm
5cm
敬请指导!
