北师大版六年级数学下册课件 第5单元 总复习5.9 正比例与反比例(29张ppt)
文档属性
| 名称 | 北师大版六年级数学下册课件 第5单元 总复习5.9 正比例与反比例(29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 11:00:10 | ||
图片预览








文档简介
(共29张PPT)
第9课时 正比例与反比例
理解正、反比例的含义。(重点)
根据正、反比例的特点解决实际问题。 (难点)
(1)好处:用字母能简明地表示数量、数量
关系、计算公式、运算律等,为
研究和解决问题带来很多方便。
(2)解方程的依据等式的性质。
(3)方程的意义:为了求未知数,利用某
种数量关系,在已知数
与未知数之间建立的等
式关系就是方程。
(4)方程解决实际问题的步骤是:
①(弄清题意,找出未知数并用 x 表示
(也可以设某个间接量为 x,再通过这个
量去求未知数)。
②根据题中数量间的相等关系列出方程。
③根据等式的性质解方程,求出方程中的
未知数。
④检验写答。
知识点
正比例与反比例
(选自教材P83 T1)举例说明什么是比,什么是比例,以及它们的应用。
两个数相除又叫两个数的比。
表示两个比相等的式子叫作比例。
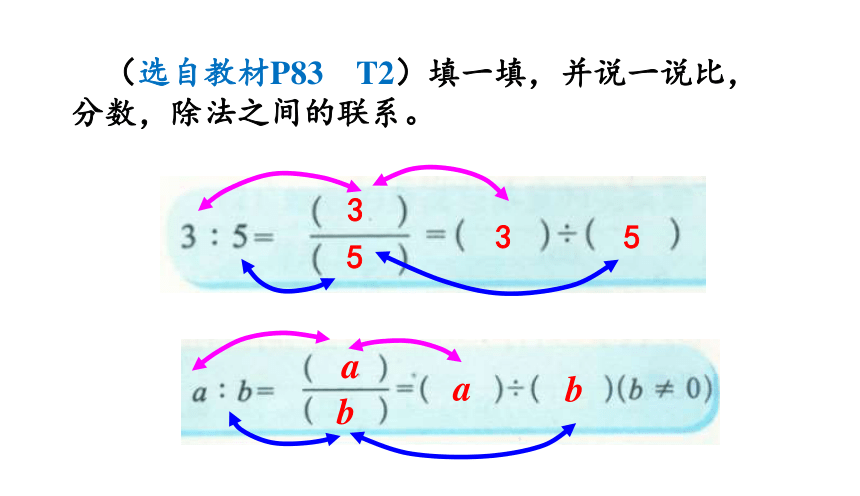
(选自教材P83 T2)填一填,并说一说比,分数,除法之间的联系。
3
5
3
5
a
b
a
b
比表示两个数相除,比的前项相当于被除数,比的后项相当于除法,比号相当于除号,分数的分子相当于被除数或比的前项,分数的分母相当于除数或比的后项,分数线相当于除号或比号。
(选自教材P83 T3)。
(1)图上距离1 cm表示实际距离6000 cm,即是60 m。
(2)240m=24000cm
答:在图上应画4cm。
60×30=1800(m2)
答:它的实际占地面积是1800m2。
正比例示例:播撒种子时,种子越多,播
种的天数就越多。
反比例示例:从A点走到B点,距离一定时,走
的速度越快,所用的时间就越短。
一辆汽车在高速公路上行驶,速度保持在100千米 / 时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
200
300
400
500
根据表格中填写的数据,描写方程图中的个点,并连线。
S÷t=100
(4)判断路程与时间是否成正比例,说说你是
怎么想的。
答:路程与时间成正比例。
因为路程随着时间的变化而变化,而且路程与时间的比值是相等,都是100。
1、(选自教材P84 T1)填一填。
(1)两个正方形的边长是1∶3,周长比是
( ),面积比是( )。
(2)9元可以买2kg鸡蛋,总价与数量的比是
( ),比值是( )。
(3)汽车3时行150km,路程与时间的比是
( ),比值是( )。
1:3
1:9
9:2
4.5
50:1
50
2、(选自教材P84 T2)化简。
30∶120
=6
2.5∶6
=25∶60
=5∶12
0.5∶3.2
=5∶32
=30
3、(选自教材P85 T6)下面表格中的两个量是否成
正比例或反比例?为什么?
答:成反比例。
答:不成比例。
答:成反比例。
4、(选自教材P85 T7)磁悬浮列车均匀行驶时,路程与
时间的关系如下。
(2)答:在。
(3)7×2.5=17.5(km)
答:行驶的路程是17.5km。
作业:完成教材相关练习题。
第9课时 正比例与反比例
理解正、反比例的含义。(重点)
根据正、反比例的特点解决实际问题。 (难点)
(1)好处:用字母能简明地表示数量、数量
关系、计算公式、运算律等,为
研究和解决问题带来很多方便。
(2)解方程的依据等式的性质。
(3)方程的意义:为了求未知数,利用某
种数量关系,在已知数
与未知数之间建立的等
式关系就是方程。
(4)方程解决实际问题的步骤是:
①(弄清题意,找出未知数并用 x 表示
(也可以设某个间接量为 x,再通过这个
量去求未知数)。
②根据题中数量间的相等关系列出方程。
③根据等式的性质解方程,求出方程中的
未知数。
④检验写答。
知识点
正比例与反比例
(选自教材P83 T1)举例说明什么是比,什么是比例,以及它们的应用。
两个数相除又叫两个数的比。
表示两个比相等的式子叫作比例。
(选自教材P83 T2)填一填,并说一说比,分数,除法之间的联系。
3
5
3
5
a
b
a
b
比表示两个数相除,比的前项相当于被除数,比的后项相当于除法,比号相当于除号,分数的分子相当于被除数或比的前项,分数的分母相当于除数或比的后项,分数线相当于除号或比号。
(选自教材P83 T3)。
(1)图上距离1 cm表示实际距离6000 cm,即是60 m。
(2)240m=24000cm
答:在图上应画4cm。
60×30=1800(m2)
答:它的实际占地面积是1800m2。
正比例示例:播撒种子时,种子越多,播
种的天数就越多。
反比例示例:从A点走到B点,距离一定时,走
的速度越快,所用的时间就越短。
一辆汽车在高速公路上行驶,速度保持在100千米 / 时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
200
300
400
500
根据表格中填写的数据,描写方程图中的个点,并连线。
S÷t=100
(4)判断路程与时间是否成正比例,说说你是
怎么想的。
答:路程与时间成正比例。
因为路程随着时间的变化而变化,而且路程与时间的比值是相等,都是100。
1、(选自教材P84 T1)填一填。
(1)两个正方形的边长是1∶3,周长比是
( ),面积比是( )。
(2)9元可以买2kg鸡蛋,总价与数量的比是
( ),比值是( )。
(3)汽车3时行150km,路程与时间的比是
( ),比值是( )。
1:3
1:9
9:2
4.5
50:1
50
2、(选自教材P84 T2)化简。
30∶120
=6
2.5∶6
=25∶60
=5∶12
0.5∶3.2
=5∶32
=30
3、(选自教材P85 T6)下面表格中的两个量是否成
正比例或反比例?为什么?
答:成反比例。
答:不成比例。
答:成反比例。
4、(选自教材P85 T7)磁悬浮列车均匀行驶时,路程与
时间的关系如下。
(2)答:在。
(3)7×2.5=17.5(km)
答:行驶的路程是17.5km。
作业:完成教材相关练习题。
