人教版B版(2019)高中数学必修第一册:第二章 等式与不等式 综合测试 (Word含答案与解析)
文档属性
| 名称 | 人教版B版(2019)高中数学必修第一册:第二章 等式与不等式 综合测试 (Word含答案与解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 801.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-22 00:00:00 | ||
图片预览




文档简介
第二章综合测试
一、单选题(本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.二次三项式分解因式为,则的值分别为( )
A.
B.
C.
D.
2.不等式的解集是( )
A.
B.
C.
D.
3.已知是的三条边,且满足,则一定是( )
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
4.已知且,则的取值范围是( )
A.
B.
C.
D.
5.已知,若关于的不等式的解集中的整数恰有3个,则( )
A.
B.
C.
D.
6.在上定义运算:,若使得成立,则实数的取值范围是( )
A.
B.
C.
D.
7.某车间分批生产某种产品,每批的生产准备费用为800元若每批生产件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
A.60件
B.80件
C.100件
D.120件
8.若两个正实数满足,且不等式有解,则实数的取值范围是( )
A.
B.
C.
D.
9.已知不等式的解集为 ,则不等式的解集为( )
A.
B.
C.
D.
二、多选题(本大题共3小题,每小题5分,共15分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
10.下列不等式推理正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
E.若,,则
11.已知,则( )
A
B.
C.
D.
E.
12.若正实数满足,则下列说法正确的是( )
A.
B.
C.
D.
三、填空题(本大题共4小题,每小题5分,共20分。将答案填在题中横线上)
13.关于的不等式的解集是,则关于的不等式的解集是________.
14.阅读理解:
(1)特例运算:①________,
②________;
(2)归纳结论:(________)________;
(3)尝试运用:直接写出计算结果________;
(4)解决问题:根据你的理解,把下列多项式因式分解:
①________,
②________;
(5)拓展延伸:若可分解为两个一次因式的积,则整数的所有可能值是________.
15.某辆汽车以的速度在高速公路上匀速行驶(考虑到高速公路行车安全,要求)时,每小时的油耗(所需要的汽油量)为号,其中为常数.当汽车以的速度行驶时,每小时的油耗为,欲使每小时的油耗不超过,则速度的取值范围为________.
16.在实数集R中定义一种运算“*”,具有性质:
(1)对任意;
(2)对任意;
(3)对任意.
则函数的最小值为________.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
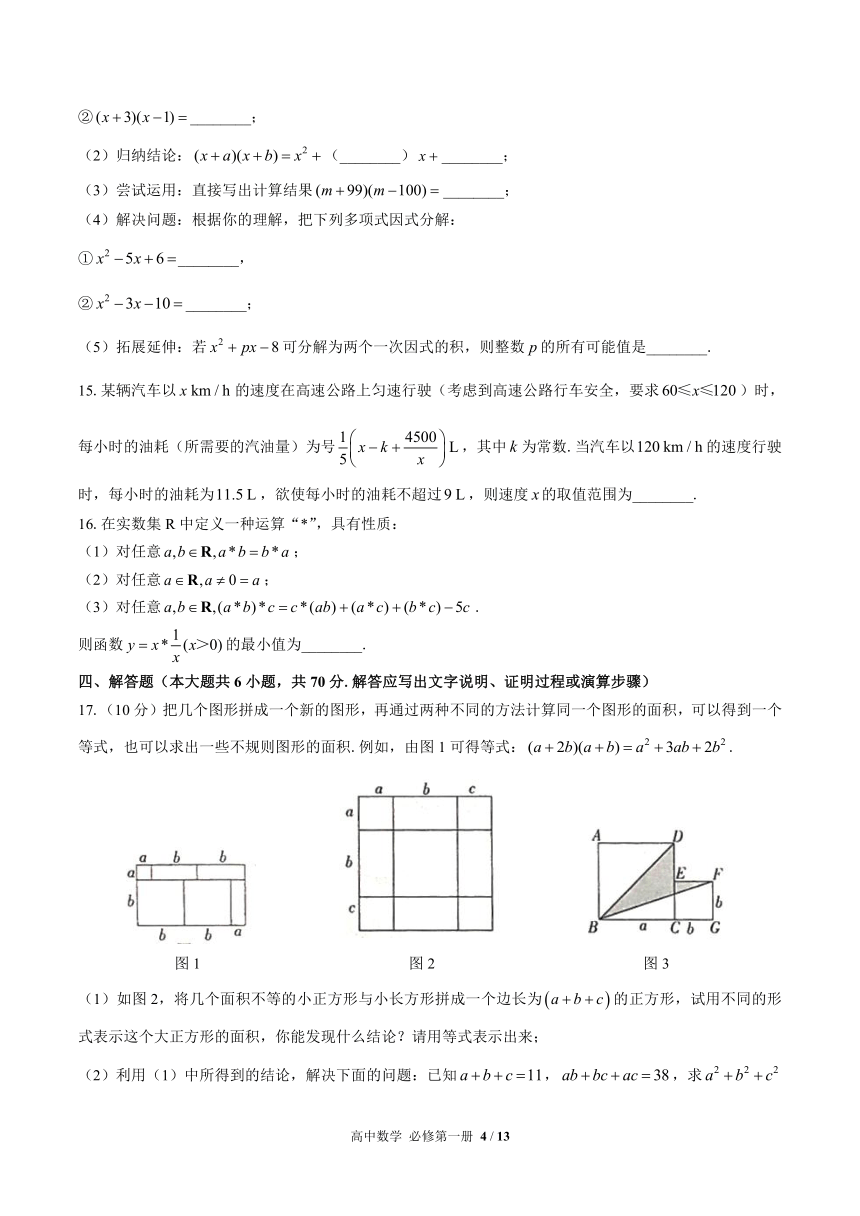
17.(10分)把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.例如,由图1可得等式:.
图1 图2 图3
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来;
(2)利用(1)中所得到的结论,解决下面的问题:已知,,求的值;
(3)如图3,将两个边长分别为和的正方形拼在一起,三点在同一直线上,连接和.这两个正方形的边长满足,,请求出阴影部分的面积.
18.(12分)解关于的不等式.
19.(12分)已知不等式的解集为..
(1)求的值;
(2)求函数的最小值.
20.(12分)已知方程的两个根是,那么,反过来,如果,那么以为两根的一元二次方程是.请根据以上结论,解决下列问题:
(1)已知关于的方程,求一个一元二次方程,使它的两根分别是已知方程两根的倒数;
(2)已知满足,求的值;
(3)已知均为实数,且,,求正数的最小值.
21.(12分)问题情境:我们知道,若一个矩形的周长固定,当其相邻两边相等,即为正方形时,面积是最大的,反过来,若一个矩形的面积固定,它的周长是否会有最值呢?
用两条直角边边长分别为的四个全等的直角三角形可以拼成一个正方形.若,可以拼成如图①
的正方形,从而得到,即;若,可以拼成如图②的正方形,从而得到,即.于是我们可以得到结论:为正数时,总有,且当时,代数式取得最小值.
图① 图②
另外,我们也可以通过代数式运算得到类似上面的结论.
,.对于任意实数,总有,且当时,代数式取得最小值.
(1)探究方法:
仿照上面的方法,对于正数,试比较和的大小关系;
(2)类比应用:
利用上面所得到的结论,完成填空:
(i)________,代数式有最值,为________;
(ii)当时,________,代数式有最________值,为________;
(iii)当时,________,代表式有最________值,为________;
(3)问题解决:
若一个矩形的面积固定为n,则它的周长是否会有最值呢?若有,求出周长的最值及此时矩形的长和宽;若没有,请说明理由,由此你能得到怎样的结论?
22.(12分)某学校为了支持生物课程基地研究植物的生长规律,计划利用学校空地建造一间室内面积为的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔,三块矩形区域的前、后与内墙各保留宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留宽的通道,如图.设矩形温室的室内长为(单位:),三块种植植物的矩形区域的总面积为(单位:).
(1)求关于的函数关系式;
(2)求的最大值
第二章综合测试
答案解析
一、
1.【答案】D
【解析】,故选C.
2.【答案】C
【解析】当时,成立;当时,原不等式等价与,即.∴原不等式的解集为.
3.【答案】A
【解析】等式变形为,即,即,∴为等腰三角形.故选A.
4.【答案】D
【解析】用特定系数法,设,则解得所以,因为,,所以,.,所以.故选D.
5.【答案】C
【解析】由,整理可得,由于该不等式的解集中的整数恰有3个,则有,此时,而,故,由不等式解得,即,而,要使该不等式的解集中的整数恰有3个,那么,由得,则有,即,解得,由得,解得,则.
6.【答案】A
【解析】由题知.
∴若,使得不等式成立,则需函数的最大值大于1,即时,成立,解得或.故选A.
7.【答案】B
【解析】若每批生产件产品,则每件产品的生产准备费用是元,仓储费用是元,总的费用是元,当且仅当,即时取等号。
8.【答案】B
∵不等式有解,,,且,,当且仅当,即时取等号,,,即.解得或,故实数的取值范围是.
9.【答案】D
【解析】不等式的解集为,所以与之对应的二次方程的两个根为1,2,由根与系数的关系得,,所以不等式化为,即,解得,所以所求不等式的解集为.
二、
10.【答案】DE
【解析】A中,例如,此时,所以A不正确;B中,若,则,则,所以B不正确;C中,例如,此时,所以C不正确;D中,若,则,则,则,所以D正确;E中,根据不等式的可加性可知E正确.故选DE.
11.【答案】DE
【解析】由,可知,由不等式的性质可知,所以,故D正确;,故E正确.故选DE.
12.【答案】CD
【解析】,且,,,∴A错误;,,B错误;,C正确;,D正确.故选CD.
三、
13.【答案】
【解析】由于不等式的解集是,所以且,故.所求不等式可化为,解得.
14.【答案】(1)① ②
(2)
(3)
(4)① ②
(5)
【解析】(1)特例运算:①,
②.
(2)归纳结论:.
(3)尝试运用:直接写出计算结果.
(4)解决问题:根据你的理解,把下列多项式因式分解:
①,
②.
(5)拓展延伸:若可分解为两个一次因式的积,则整数的所有可能值是.
15.【答案】
【解析】解析因为“汽车以的速度行驶时,每小时的油耗为”,所以.解得.故汽车以的速度在高速公路上匀速行使时,每小时的油耗为.依题意号,解得,因为,所以,所以欲使每小时的油耗不超过,速度的取值范围为.
16.【答案】3
【解析】对任意,令,
代入得.
由可得,由可得,所以,因为,由均值不等式可得(当且仅当,即时,等号成立).所以的最小值为3.
四、
17.【答案】(1).
(2),,
.
(3),
18.【答案】可化为.当,即时,,此时;当,即时,解得或;当,即时,解得或.
综上所述,当时,;当时,;当时,.
19.【答案】(l):不等式的解集为,
∴1和是方程的两根,
∴,解得
(2)由(1)得,当且仅当,即时,等号成立,∴函数的最小值为12.
20.【答案】(1)设方程,的两个根分别是,则,,∴,若一个一元二次方程的两个根分别是已知方程两根的倒数,则这个一元二次方程式,整理得.
(2)分两种情况讨论:①当时,∵满足,
∴是的两个根,∴,,
∴.
②当时,.
(3)∵
,
∴是方程的两个根.
∴,即.
∵是正数,∴,
∴正数的最小值是4.
21.【答案】(1)∵当均为正数时,,
∴,当且仅当时,取等号.
(2)(i)结合探究方法中得出的结论可知,,所以代数式,有最小值,为2.
故答案为;小;2.
(ii)结合探究方法中得出的结论可知,当时,代数式有最小值,为6.
故答案为;小;6.
(ii)结合探究方法中得出的结论可知,当时,代数式有最小值为,故答案为;小;.
(3)设该矩形的长为,宽为,根据题意知:周长,且当时,代数式取得最小值为,此时.
故若一个矩形的面积固定为,则它的周长有最小值,周长的最小值为,此时矩形的长和宽均为。
22【答案】(1)由题得,
(2)因为,所以,当且仅当时,等号成立,所以.
故当矩形温室的室内长为时,三块种植植物的矩形区域的总面积最大,为.
高中数学 必修第一册 7 / 7
一、单选题(本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.二次三项式分解因式为,则的值分别为( )
A.
B.
C.
D.
2.不等式的解集是( )
A.
B.
C.
D.
3.已知是的三条边,且满足,则一定是( )
A.等腰三角形
B.等边三角形
C.直角三角形
D.等腰直角三角形
4.已知且,则的取值范围是( )
A.
B.
C.
D.
5.已知,若关于的不等式的解集中的整数恰有3个,则( )
A.
B.
C.
D.
6.在上定义运算:,若使得成立,则实数的取值范围是( )
A.
B.
C.
D.
7.某车间分批生产某种产品,每批的生产准备费用为800元若每批生产件,则平均仓储时间为天,且每件产品每天的仓储费用为1元.为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品( )
A.60件
B.80件
C.100件
D.120件
8.若两个正实数满足,且不等式有解,则实数的取值范围是( )
A.
B.
C.
D.
9.已知不等式的解集为 ,则不等式的解集为( )
A.
B.
C.
D.
二、多选题(本大题共3小题,每小题5分,共15分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
10.下列不等式推理正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
E.若,,则
11.已知,则( )
A
B.
C.
D.
E.
12.若正实数满足,则下列说法正确的是( )
A.
B.
C.
D.
三、填空题(本大题共4小题,每小题5分,共20分。将答案填在题中横线上)
13.关于的不等式的解集是,则关于的不等式的解集是________.
14.阅读理解:
(1)特例运算:①________,
②________;
(2)归纳结论:(________)________;
(3)尝试运用:直接写出计算结果________;
(4)解决问题:根据你的理解,把下列多项式因式分解:
①________,
②________;
(5)拓展延伸:若可分解为两个一次因式的积,则整数的所有可能值是________.
15.某辆汽车以的速度在高速公路上匀速行驶(考虑到高速公路行车安全,要求)时,每小时的油耗(所需要的汽油量)为号,其中为常数.当汽车以的速度行驶时,每小时的油耗为,欲使每小时的油耗不超过,则速度的取值范围为________.
16.在实数集R中定义一种运算“*”,具有性质:
(1)对任意;
(2)对任意;
(3)对任意.
则函数的最小值为________.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(10分)把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.例如,由图1可得等式:.
图1 图2 图3
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来;
(2)利用(1)中所得到的结论,解决下面的问题:已知,,求的值;
(3)如图3,将两个边长分别为和的正方形拼在一起,三点在同一直线上,连接和.这两个正方形的边长满足,,请求出阴影部分的面积.
18.(12分)解关于的不等式.
19.(12分)已知不等式的解集为..
(1)求的值;
(2)求函数的最小值.
20.(12分)已知方程的两个根是,那么,反过来,如果,那么以为两根的一元二次方程是.请根据以上结论,解决下列问题:
(1)已知关于的方程,求一个一元二次方程,使它的两根分别是已知方程两根的倒数;
(2)已知满足,求的值;
(3)已知均为实数,且,,求正数的最小值.
21.(12分)问题情境:我们知道,若一个矩形的周长固定,当其相邻两边相等,即为正方形时,面积是最大的,反过来,若一个矩形的面积固定,它的周长是否会有最值呢?
用两条直角边边长分别为的四个全等的直角三角形可以拼成一个正方形.若,可以拼成如图①
的正方形,从而得到,即;若,可以拼成如图②的正方形,从而得到,即.于是我们可以得到结论:为正数时,总有,且当时,代数式取得最小值.
图① 图②
另外,我们也可以通过代数式运算得到类似上面的结论.
,.对于任意实数,总有,且当时,代数式取得最小值.
(1)探究方法:
仿照上面的方法,对于正数,试比较和的大小关系;
(2)类比应用:
利用上面所得到的结论,完成填空:
(i)________,代数式有最值,为________;
(ii)当时,________,代数式有最________值,为________;
(iii)当时,________,代表式有最________值,为________;
(3)问题解决:
若一个矩形的面积固定为n,则它的周长是否会有最值呢?若有,求出周长的最值及此时矩形的长和宽;若没有,请说明理由,由此你能得到怎样的结论?
22.(12分)某学校为了支持生物课程基地研究植物的生长规律,计划利用学校空地建造一间室内面积为的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔,三块矩形区域的前、后与内墙各保留宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留宽的通道,如图.设矩形温室的室内长为(单位:),三块种植植物的矩形区域的总面积为(单位:).
(1)求关于的函数关系式;
(2)求的最大值
第二章综合测试
答案解析
一、
1.【答案】D
【解析】,故选C.
2.【答案】C
【解析】当时,成立;当时,原不等式等价与,即.∴原不等式的解集为.
3.【答案】A
【解析】等式变形为,即,即,∴为等腰三角形.故选A.
4.【答案】D
【解析】用特定系数法,设,则解得所以,因为,,所以,.,所以.故选D.
5.【答案】C
【解析】由,整理可得,由于该不等式的解集中的整数恰有3个,则有,此时,而,故,由不等式解得,即,而,要使该不等式的解集中的整数恰有3个,那么,由得,则有,即,解得,由得,解得,则.
6.【答案】A
【解析】由题知.
∴若,使得不等式成立,则需函数的最大值大于1,即时,成立,解得或.故选A.
7.【答案】B
【解析】若每批生产件产品,则每件产品的生产准备费用是元,仓储费用是元,总的费用是元,当且仅当,即时取等号。
8.【答案】B
∵不等式有解,,,且,,当且仅当,即时取等号,,,即.解得或,故实数的取值范围是.
9.【答案】D
【解析】不等式的解集为,所以与之对应的二次方程的两个根为1,2,由根与系数的关系得,,所以不等式化为,即,解得,所以所求不等式的解集为.
二、
10.【答案】DE
【解析】A中,例如,此时,所以A不正确;B中,若,则,则,所以B不正确;C中,例如,此时,所以C不正确;D中,若,则,则,则,所以D正确;E中,根据不等式的可加性可知E正确.故选DE.
11.【答案】DE
【解析】由,可知,由不等式的性质可知,所以,故D正确;,故E正确.故选DE.
12.【答案】CD
【解析】,且,,,∴A错误;,,B错误;,C正确;,D正确.故选CD.
三、
13.【答案】
【解析】由于不等式的解集是,所以且,故.所求不等式可化为,解得.
14.【答案】(1)① ②
(2)
(3)
(4)① ②
(5)
【解析】(1)特例运算:①,
②.
(2)归纳结论:.
(3)尝试运用:直接写出计算结果.
(4)解决问题:根据你的理解,把下列多项式因式分解:
①,
②.
(5)拓展延伸:若可分解为两个一次因式的积,则整数的所有可能值是.
15.【答案】
【解析】解析因为“汽车以的速度行驶时,每小时的油耗为”,所以.解得.故汽车以的速度在高速公路上匀速行使时,每小时的油耗为.依题意号,解得,因为,所以,所以欲使每小时的油耗不超过,速度的取值范围为.
16.【答案】3
【解析】对任意,令,
代入得.
由可得,由可得,所以,因为,由均值不等式可得(当且仅当,即时,等号成立).所以的最小值为3.
四、
17.【答案】(1).
(2),,
.
(3),
18.【答案】可化为.当,即时,,此时;当,即时,解得或;当,即时,解得或.
综上所述,当时,;当时,;当时,.
19.【答案】(l):不等式的解集为,
∴1和是方程的两根,
∴,解得
(2)由(1)得,当且仅当,即时,等号成立,∴函数的最小值为12.
20.【答案】(1)设方程,的两个根分别是,则,,∴,若一个一元二次方程的两个根分别是已知方程两根的倒数,则这个一元二次方程式,整理得.
(2)分两种情况讨论:①当时,∵满足,
∴是的两个根,∴,,
∴.
②当时,.
(3)∵
,
∴是方程的两个根.
∴,即.
∵是正数,∴,
∴正数的最小值是4.
21.【答案】(1)∵当均为正数时,,
∴,当且仅当时,取等号.
(2)(i)结合探究方法中得出的结论可知,,所以代数式,有最小值,为2.
故答案为;小;2.
(ii)结合探究方法中得出的结论可知,当时,代数式有最小值,为6.
故答案为;小;6.
(ii)结合探究方法中得出的结论可知,当时,代数式有最小值为,故答案为;小;.
(3)设该矩形的长为,宽为,根据题意知:周长,且当时,代数式取得最小值为,此时.
故若一个矩形的面积固定为,则它的周长有最小值,周长的最小值为,此时矩形的长和宽均为。
22【答案】(1)由题得,
(2)因为,所以,当且仅当时,等号成立,所以.
故当矩形温室的室内长为时,三块种植植物的矩形区域的总面积最大,为.
高中数学 必修第一册 7 / 7
