高中物理人教新版导学案 选择性必修 第2 册第2章 电磁感应的综合问题 Word版含解析
文档属性
| 名称 | 高中物理人教新版导学案 选择性必修 第2 册第2章 电磁感应的综合问题 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 362.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-20 13:31:59 | ||
图片预览


文档简介
电磁感应的综合问题
专题解读 1.本专题是运动学、动力学、恒定电流、电磁感应和能量等知识的综合应用,高考既以选择题的形式命题,也以计算题的形式命题.
2.学好本专题,可以极大地培养同学们数形结合的推理能力和电路分析能力,针对性的专题强化,可以提升同学们解决数形结合、利用动力学和功能关系解决电磁感应问题的信心.
3.用到的知识有:左手定则、安培定则、右手定则、楞次定律、法拉第电磁感应定律、闭合电路欧姆定律、平衡条件、牛顿运动定律、函数图像、动能定理和能量守恒定律等.
1.题型简述
借助图像考查电磁感应的规律,一直是高考的热点,此类题目一般分为两类:
(1)由给定的电磁感应过程选出正确的图像;
(2)由给定的图像分析电磁感应过程,定性或定量求解相应的物理量或推断出其他图像.常见的图像有B-t图、E-t图、i-t图、v-t图及F-t图等.
2.解题关键
弄清初始条件、正负方向的对应变化范围、所研究物理量的函数表达式、进出磁场的转折点等是解决此类问题的关键.
3.解题步骤
(1)明确图像的种类,即是B-t图还是Φ-t图,或者E-t图、I-t图等;
(2)分析电磁感应的具体过程;
(3)用右手定则或楞次定律确定方向的对应关系;
(4)结合法拉第电磁感应定律、闭合电路欧姆定律、牛顿运动定律等知识写出相应的函数关系式;
(5)根据函数关系式,进行数学分析,如分析斜率的变化、截距等;
(6)画图像或判断图像.
4.常用方法
(1)排除法:定性地分析电磁感应过程中物理量的变化趋势(增大还是减小)、变化快慢(均匀变化还是非均匀变化),特别是分析物理量的正负,以排除错误的选项.
(2)函数法:根据题目所给条件定量地写出两个物理量之间的函数关系,然后由函数关系对图像进行分析和判断.
类型1 动生问题
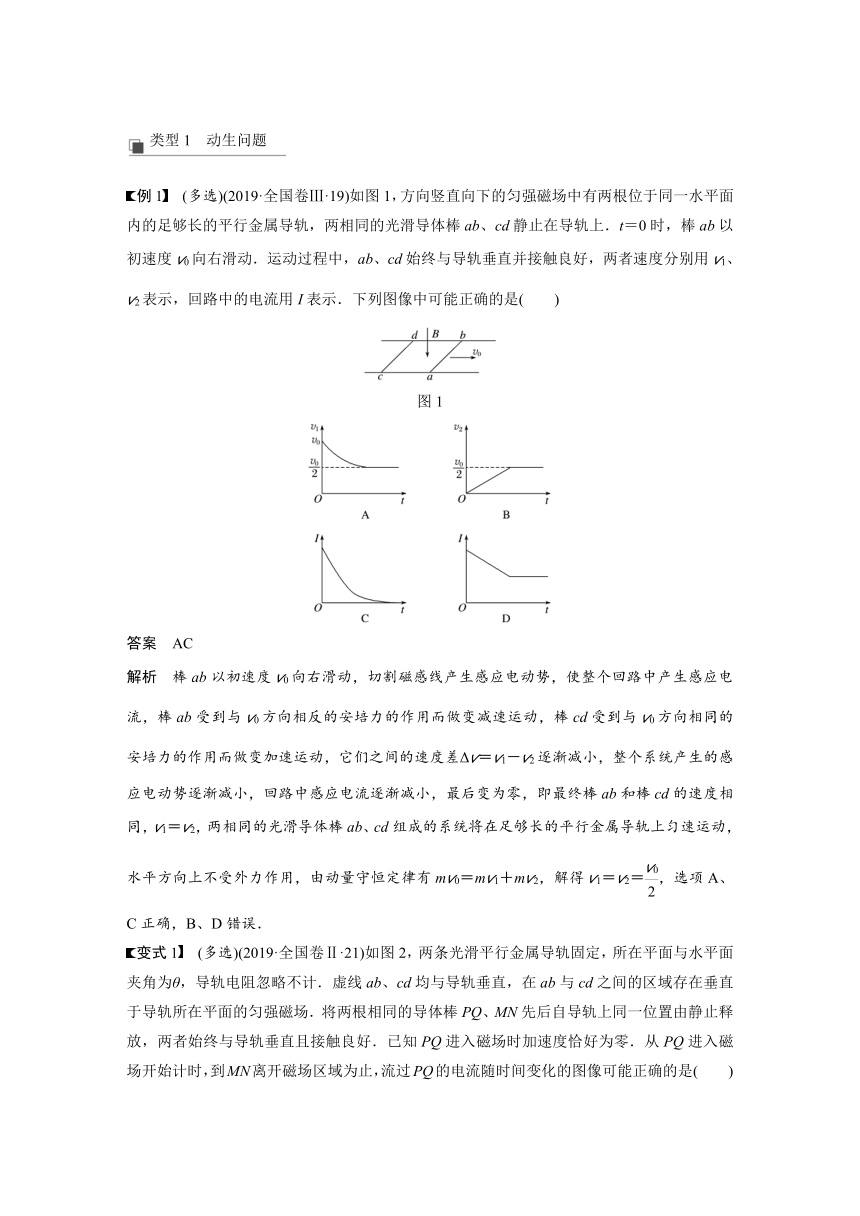
例1 (多选)(2019·全国卷Ⅲ·19)如图1,方向竖直向下的匀强磁场中有两根位于同一水平面内的足够长的平行金属导轨,两相同的光滑导体棒ab、cd静止在导轨上.t=0时,棒ab以初速度v0向右滑动.运动过程中,ab、cd始终与导轨垂直并接触良好,两者速度分别用v1、v2表示,回路中的电流用I表示.下列图像中可能正确的是( )
图1
答案 AC
解析 棒ab以初速度v0向右滑动,切割磁感线产生感应电动势,使整个回路中产生感应电流,棒ab受到与v0方向相反的安培力的作用而做变减速运动,棒cd受到与v0方向相同的安培力的作用而做变加速运动,它们之间的速度差Δv=v1-v2逐渐减小,整个系统产生的感应电动势逐渐减小,回路中感应电流逐渐减小,最后变为零,即最终棒ab和棒cd的速度相同,v1=v2,两相同的光滑导体棒ab、cd组成的系统将在足够长的平行金属导轨上匀速运动,水平方向上不受外力作用,由动量守恒定律有mv0=mv1+mv2,解得v1=v2=,选项A、C正确,B、D错误.
变式1 (多选)(2019·全国卷Ⅱ·21)如图2,两条光滑平行金属导轨固定,所在平面与水平面夹角为θ,导轨电阻忽略不计.虚线ab、cd均与导轨垂直,在ab与cd之间的区域存在垂直于导轨所在平面的匀强磁场.将两根相同的导体棒PQ、MN先后自导轨上同一位置由静止释放,两者始终与导轨垂直且接触良好.已知PQ进入磁场时加速度恰好为零.从PQ进入磁场开始计时,到MN离开磁场区域为止,流过PQ的电流随时间变化的图像可能正确的是( )
图2
答案 AD
解析 根据题述,PQ进入磁场时加速度恰好为零,两导体棒从同一位置释放,则两导体棒进入磁场时的速度相同,产生的感应电动势大小相等,若释放两导体棒的时间间隔足够长,在PQ通过磁场区域一段时间后MN进入磁场区域,根据法拉第电磁感应定律和闭合电路欧姆定律可知流过PQ的电流随时间变化的图像可能是A;若释放两导体棒的时间间隔较短,在PQ没有出磁场区域时MN就进入磁场区域,则两棒在磁场区域中运动时回路中磁通量不变,两棒不受安培力作用,二者在磁场中做加速运动,PQ出磁场后,MN切割磁感线产生感应电动势和感应电流,且感应电流一定大于I1,受到安培力作用,由于安培力与速度成正比,则MN所受的安培力一定大于MN的重力沿导轨平面方向的分力,所以MN一定做减速运动,回路中感应电流减小,流过PQ的电流随时间变化的图像可能是D.
类型2 感生问题
例2 (2019·广东广州市下学期一模)如图3甲所示,梯形硬导线框abcd固定在磁场中,磁场方向与线框平面垂直,图乙表示该磁场的磁感应强度B随时间t变化的关系图,t=0时刻磁场方向垂直纸面向里.在0~5t0时间内,设垂直ab边向上为安培力的正方向,线框ab边受到该磁场对它的安培力F随时间t变化的关系图为( )
图3
答案 D
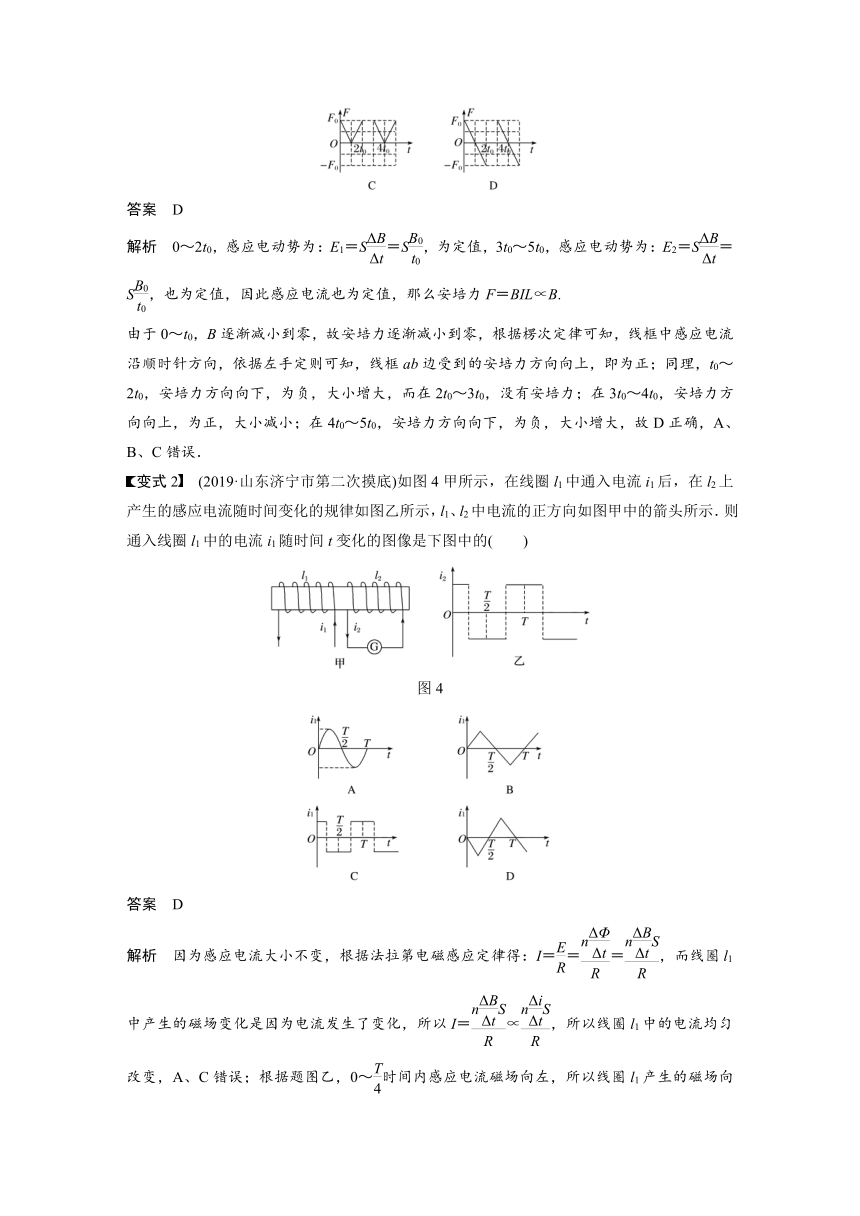
解析 0~2t0,感应电动势为:E1=S=S,为定值,3t0~5t0,感应电动势为:E2=S=S,也为定值,因此感应电流也为定值,那么安培力F=BIL∝B.
由于0~t0,B逐渐减小到零,故安培力逐渐减小到零,根据楞次定律可知,线框中感应电流沿顺时针方向,依据左手定则可知,线框ab边受到的安培力方向向上,即为正;同理,t0~2t0,安培力方向向下,为负,大小增大,而在2t0~3t0,没有安培力;在3t0~4t0,安培力方向向上,为正,大小减小;在4t0~5t0,安培力方向向下,为负,大小增大,故D正确,A、B、C错误.
变式2 (2019·山东济宁市第二次摸底)如图4甲所示,在线圈l1中通入电流i1后,在l2上产生的感应电流随时间变化的规律如图乙所示,l1、l2中电流的正方向如图甲中的箭头所示.则通入线圈l1中的电流i1随时间t变化的图像是下图中的( )
图4
答案 D
解析 因为感应电流大小不变,根据法拉第电磁感应定律得:I===,而线圈l1中产生的磁场变化是因为电流发生了变化,所以I=∝,所以线圈l1中的电流均匀改变,A、C错误;根据题图乙,0~时间内感应电流磁场向左,所以线圈l1产生的磁场向左减小,或向右增大,B错误,D正确.
1.题型简述
感应电流在磁场中受到安培力的作用,因此电磁感应问题往往跟力学问题联系在一起.解决这类问题需要综合应用电磁感应规律(法拉第电磁感应定律、楞次定律)及力学中的有关规律(共点力的平衡条件、牛顿运动定律、动能定理等).
2.处理方法
状态 特征 处理方法
平衡态 加速度为零 根据平衡条件列式分析
非平衡态 加速度不为零 根据牛顿第二定律进行动态分析或结合功能关系进行分析
3.基本思路
解决这类问题的关键是通过运动状态的分析,寻找过程中的临界状态,如速度、加速度最大值或最小值的条件.具体思路如下:
→→→
例3 (2019·四川省综合能力提升卷(三))如图5所示,两根足够长光滑平行金属导轨间距l=0.9 m,与水平面夹角θ=30°,正方形区域abcd内有匀强磁场,磁感应强度B=2 T,方向垂直于斜面向上,甲、乙是两根质量相同、电阻均为R=4.86 Ω的金属杆,垂直于导轨放置.甲置于磁场的上边界ab处,乙置于甲上方l处,现将两金属杆由静止同时释放,并立即在甲上施加一个沿导轨方向的拉力F,甲始终以a=5 m/s2的加速度沿导轨匀加速运动,乙进入磁场时恰好做匀速运动,g=10 m/s2.计算:
图5
(1)每根金属杆的质量m;
(2)拉力F的最大值;
(3)乙到达磁场下边界时两杆间的距离及乙穿过磁场的过程中电路产生的热量.
答案 (1)0.2 kg (2)1 N (3)0.225 m 0.9 J
解析 (1)由题意得:乙进入磁场前做初速度为零的匀加速直线运动,加速度:a′==5 m/s2;
乙进入磁场时的速度:v′==3 m/s
乙进入磁场后做匀速直线运动,由平衡条件得:mgsin θ=
解得:m=0.2 kg
(2)因甲、乙下滑的加速度相等,可知当甲在磁场中滑动时,乙还未进入磁场,则甲在磁场中受到的安培力:F安=BIl=
由牛顿第二定律可得:F+mgsin θ-=ma
甲做匀加速直线运动,v逐渐增大,则拉力F逐渐变大.
当甲滑到cd位置时导体棒的速度最大,F最大,此时甲的速度v==3 m/s,
代入数据解得:F=1 N
(3)乙从进入磁场到到达磁场下边界的时间t== s=0.3 s;
当乙进入磁场时,甲刚好出磁场,速度为v=3 m/s,甲出磁场后的加速度仍为5 m/s2,则t=0.3 s内的位移x甲=vt+at2=1.125 m,
则此时甲、乙两棒相距Δx=x甲-l=0.225 m
乙穿过磁场过程产生的热量等于乙机械能的减小量:Q=mglsin 30°=0.2×10×0.9×0.5 J=0.9 J.
变式3 (2016·全国卷Ⅱ·24)如图6,水平面(纸面)内间距为l的平行金属导轨间接一电阻,质量为m、长度为l的金属杆置于导轨上.t=0时,金属杆在水平向右、大小为F的恒定拉力作用下由静止开始运动.t0时刻,金属杆进入磁感应强度大小为B、方向垂直于纸面向里的匀强磁场区域,且在磁场中恰好能保持匀速运动.杆与导轨的电阻均忽略不计,两者始终保持垂直且接触良好,两者之间的动摩擦因数为μ.重力加速度大小为g.求:
图6
(1)金属杆在磁场中运动时产生的电动势的大小;
(2)电阻的阻值.
答案 (1)Blt0(-μg) (2)
解析 (1)设金属杆进入磁场前的加速度大小为a,由牛顿第二定律得F-μmg=ma①
设金属杆到达磁场左边界时的速度为v,由运动学公式有v=at0②
当金属杆以速度v在磁场中运动时,由法拉第电磁感应定律知产生的电动势为E=Blv③
联立①②③式可得
E=Blt0(-μg)④
(2)设金属杆在磁场区域中匀速运动时,金属杆中的电流为I,根据欧姆定律
I=⑤
式中R为电阻的阻值.金属杆所受的安培力为
F安=BlI⑥
因金属杆做匀速运动,有F-μmg-F安=0⑦
联立④⑤⑥⑦式得R=.
1.题型简述
电磁感应过程的实质是不同形式的能量转化的过程,而能量的转化是通过安培力做功来实现的.安培力做功的过程,是电能转化为其他形式的能的过程;外力克服安培力做功的过程,则是其他形式的能转化为电能的过程.
2.解题步骤
(1)确定研究对象(导体棒或回路);
(2)弄清电磁感应过程中,哪些力做功,哪些形式的能量相互转化;
(3)根据能量守恒定律或功能关系列式求解.
3.两类情况
(1)若回路中电流恒定,可以利用电路结构及W=UIt或Q=I2Rt直接进行计算.
(2)若电流变化,则
①利用安培力做功求解:电磁感应中产生的电能等于克服安培力所做的功;
②利用能量守恒求解:若只有电能与机械能的转化,则减少的机械能等于产生的电能.
例4 (2019·北京卷·22)如图7所示,垂直于纸面的匀强磁场磁感应强度为B.纸面内有一正方形均匀金属线框abcd,其边长为L,总电阻为R,ad边与磁场边界平行.从ad边刚进入磁场直至bc边刚要进入的过程中,线框在向左的拉力作用下以速度v匀速运动,求:
图7
(1)感应电动势的大小E;
(2)拉力做功的功率P;
(3)ab边产生的焦耳热Q.
答案 (1)BLv (2) (3)
解析 (1)由法拉第电磁感应定律可得,感应电动势
E=BLv
(2)线框中的感应电流I=
拉力大小等于安培力大小F=BIL
拉力的功率P=Fv=
(3)线框ab边电阻Rab=
时间t=
ab边产生的焦耳热Q=I2Rabt=.
变式4 (2020·宁夏银川市高三质检)如图8所示,水平放置的U形导轨足够长,置于方向竖直向上的匀强磁场中,磁感应强度大小为B=5 T,导轨宽度L=0.4 m,左侧与R=0.5 Ω的定值电阻连接,右侧有导体棒ab垂直导轨跨放在导轨上,导体棒ab质量m=2.0 kg,电阻r=0.5 Ω,与导轨间的动摩擦因数μ=0.2,其余电阻可忽略不计.导体棒ab在大小为10 N的水平外力F作用下,由静止开始运动了x=40 cm后,速度达到最大,取g=10 m/s2.求:
图8
(1)导体棒ab运动的最大速度的大小;
(2)当导体棒ab的速度v=1 m/s时,导体棒ab的加速度的大小;
(3)导体棒ab由静止运动到刚达到最大速度的过程中,电阻R上产生的热量.
答案 (1)1.5 m/s (2)1 m/s2 (3)0.075 J
解析 (1)导体棒ab垂直切割磁感线,产生的感应电动势大小:E=BLv
由闭合电路欧姆定律得:I=
可得导体棒受到的安培力:F安=BIL=
当导体棒做匀速直线运动时速度最大,由平衡条件得:+μmg=F
解得最大速度:vm=1.5 m/s;
(2)当导体棒ab的速度v=1 m/s时,由牛顿第二定律得:F--μmg=ma
解得:a=1 m/s2;
(3)导体棒ab由静止运动到刚达到最大速度的过程中,由能量守恒定律可得:Fx=Q+μmgx+mvm2
解得:Q=0.15 J
所以QR=Q=0.075 J.
专题解读 1.本专题是运动学、动力学、恒定电流、电磁感应和能量等知识的综合应用,高考既以选择题的形式命题,也以计算题的形式命题.
2.学好本专题,可以极大地培养同学们数形结合的推理能力和电路分析能力,针对性的专题强化,可以提升同学们解决数形结合、利用动力学和功能关系解决电磁感应问题的信心.
3.用到的知识有:左手定则、安培定则、右手定则、楞次定律、法拉第电磁感应定律、闭合电路欧姆定律、平衡条件、牛顿运动定律、函数图像、动能定理和能量守恒定律等.
1.题型简述
借助图像考查电磁感应的规律,一直是高考的热点,此类题目一般分为两类:
(1)由给定的电磁感应过程选出正确的图像;
(2)由给定的图像分析电磁感应过程,定性或定量求解相应的物理量或推断出其他图像.常见的图像有B-t图、E-t图、i-t图、v-t图及F-t图等.
2.解题关键
弄清初始条件、正负方向的对应变化范围、所研究物理量的函数表达式、进出磁场的转折点等是解决此类问题的关键.
3.解题步骤
(1)明确图像的种类,即是B-t图还是Φ-t图,或者E-t图、I-t图等;
(2)分析电磁感应的具体过程;
(3)用右手定则或楞次定律确定方向的对应关系;
(4)结合法拉第电磁感应定律、闭合电路欧姆定律、牛顿运动定律等知识写出相应的函数关系式;
(5)根据函数关系式,进行数学分析,如分析斜率的变化、截距等;
(6)画图像或判断图像.
4.常用方法
(1)排除法:定性地分析电磁感应过程中物理量的变化趋势(增大还是减小)、变化快慢(均匀变化还是非均匀变化),特别是分析物理量的正负,以排除错误的选项.
(2)函数法:根据题目所给条件定量地写出两个物理量之间的函数关系,然后由函数关系对图像进行分析和判断.
类型1 动生问题
例1 (多选)(2019·全国卷Ⅲ·19)如图1,方向竖直向下的匀强磁场中有两根位于同一水平面内的足够长的平行金属导轨,两相同的光滑导体棒ab、cd静止在导轨上.t=0时,棒ab以初速度v0向右滑动.运动过程中,ab、cd始终与导轨垂直并接触良好,两者速度分别用v1、v2表示,回路中的电流用I表示.下列图像中可能正确的是( )
图1
答案 AC
解析 棒ab以初速度v0向右滑动,切割磁感线产生感应电动势,使整个回路中产生感应电流,棒ab受到与v0方向相反的安培力的作用而做变减速运动,棒cd受到与v0方向相同的安培力的作用而做变加速运动,它们之间的速度差Δv=v1-v2逐渐减小,整个系统产生的感应电动势逐渐减小,回路中感应电流逐渐减小,最后变为零,即最终棒ab和棒cd的速度相同,v1=v2,两相同的光滑导体棒ab、cd组成的系统将在足够长的平行金属导轨上匀速运动,水平方向上不受外力作用,由动量守恒定律有mv0=mv1+mv2,解得v1=v2=,选项A、C正确,B、D错误.
变式1 (多选)(2019·全国卷Ⅱ·21)如图2,两条光滑平行金属导轨固定,所在平面与水平面夹角为θ,导轨电阻忽略不计.虚线ab、cd均与导轨垂直,在ab与cd之间的区域存在垂直于导轨所在平面的匀强磁场.将两根相同的导体棒PQ、MN先后自导轨上同一位置由静止释放,两者始终与导轨垂直且接触良好.已知PQ进入磁场时加速度恰好为零.从PQ进入磁场开始计时,到MN离开磁场区域为止,流过PQ的电流随时间变化的图像可能正确的是( )
图2
答案 AD
解析 根据题述,PQ进入磁场时加速度恰好为零,两导体棒从同一位置释放,则两导体棒进入磁场时的速度相同,产生的感应电动势大小相等,若释放两导体棒的时间间隔足够长,在PQ通过磁场区域一段时间后MN进入磁场区域,根据法拉第电磁感应定律和闭合电路欧姆定律可知流过PQ的电流随时间变化的图像可能是A;若释放两导体棒的时间间隔较短,在PQ没有出磁场区域时MN就进入磁场区域,则两棒在磁场区域中运动时回路中磁通量不变,两棒不受安培力作用,二者在磁场中做加速运动,PQ出磁场后,MN切割磁感线产生感应电动势和感应电流,且感应电流一定大于I1,受到安培力作用,由于安培力与速度成正比,则MN所受的安培力一定大于MN的重力沿导轨平面方向的分力,所以MN一定做减速运动,回路中感应电流减小,流过PQ的电流随时间变化的图像可能是D.
类型2 感生问题
例2 (2019·广东广州市下学期一模)如图3甲所示,梯形硬导线框abcd固定在磁场中,磁场方向与线框平面垂直,图乙表示该磁场的磁感应强度B随时间t变化的关系图,t=0时刻磁场方向垂直纸面向里.在0~5t0时间内,设垂直ab边向上为安培力的正方向,线框ab边受到该磁场对它的安培力F随时间t变化的关系图为( )
图3
答案 D
解析 0~2t0,感应电动势为:E1=S=S,为定值,3t0~5t0,感应电动势为:E2=S=S,也为定值,因此感应电流也为定值,那么安培力F=BIL∝B.
由于0~t0,B逐渐减小到零,故安培力逐渐减小到零,根据楞次定律可知,线框中感应电流沿顺时针方向,依据左手定则可知,线框ab边受到的安培力方向向上,即为正;同理,t0~2t0,安培力方向向下,为负,大小增大,而在2t0~3t0,没有安培力;在3t0~4t0,安培力方向向上,为正,大小减小;在4t0~5t0,安培力方向向下,为负,大小增大,故D正确,A、B、C错误.
变式2 (2019·山东济宁市第二次摸底)如图4甲所示,在线圈l1中通入电流i1后,在l2上产生的感应电流随时间变化的规律如图乙所示,l1、l2中电流的正方向如图甲中的箭头所示.则通入线圈l1中的电流i1随时间t变化的图像是下图中的( )
图4
答案 D
解析 因为感应电流大小不变,根据法拉第电磁感应定律得:I===,而线圈l1中产生的磁场变化是因为电流发生了变化,所以I=∝,所以线圈l1中的电流均匀改变,A、C错误;根据题图乙,0~时间内感应电流磁场向左,所以线圈l1产生的磁场向左减小,或向右增大,B错误,D正确.
1.题型简述
感应电流在磁场中受到安培力的作用,因此电磁感应问题往往跟力学问题联系在一起.解决这类问题需要综合应用电磁感应规律(法拉第电磁感应定律、楞次定律)及力学中的有关规律(共点力的平衡条件、牛顿运动定律、动能定理等).
2.处理方法
状态 特征 处理方法
平衡态 加速度为零 根据平衡条件列式分析
非平衡态 加速度不为零 根据牛顿第二定律进行动态分析或结合功能关系进行分析
3.基本思路
解决这类问题的关键是通过运动状态的分析,寻找过程中的临界状态,如速度、加速度最大值或最小值的条件.具体思路如下:
→→→
例3 (2019·四川省综合能力提升卷(三))如图5所示,两根足够长光滑平行金属导轨间距l=0.9 m,与水平面夹角θ=30°,正方形区域abcd内有匀强磁场,磁感应强度B=2 T,方向垂直于斜面向上,甲、乙是两根质量相同、电阻均为R=4.86 Ω的金属杆,垂直于导轨放置.甲置于磁场的上边界ab处,乙置于甲上方l处,现将两金属杆由静止同时释放,并立即在甲上施加一个沿导轨方向的拉力F,甲始终以a=5 m/s2的加速度沿导轨匀加速运动,乙进入磁场时恰好做匀速运动,g=10 m/s2.计算:
图5
(1)每根金属杆的质量m;
(2)拉力F的最大值;
(3)乙到达磁场下边界时两杆间的距离及乙穿过磁场的过程中电路产生的热量.
答案 (1)0.2 kg (2)1 N (3)0.225 m 0.9 J
解析 (1)由题意得:乙进入磁场前做初速度为零的匀加速直线运动,加速度:a′==5 m/s2;
乙进入磁场时的速度:v′==3 m/s
乙进入磁场后做匀速直线运动,由平衡条件得:mgsin θ=
解得:m=0.2 kg
(2)因甲、乙下滑的加速度相等,可知当甲在磁场中滑动时,乙还未进入磁场,则甲在磁场中受到的安培力:F安=BIl=
由牛顿第二定律可得:F+mgsin θ-=ma
甲做匀加速直线运动,v逐渐增大,则拉力F逐渐变大.
当甲滑到cd位置时导体棒的速度最大,F最大,此时甲的速度v==3 m/s,
代入数据解得:F=1 N
(3)乙从进入磁场到到达磁场下边界的时间t== s=0.3 s;
当乙进入磁场时,甲刚好出磁场,速度为v=3 m/s,甲出磁场后的加速度仍为5 m/s2,则t=0.3 s内的位移x甲=vt+at2=1.125 m,
则此时甲、乙两棒相距Δx=x甲-l=0.225 m
乙穿过磁场过程产生的热量等于乙机械能的减小量:Q=mglsin 30°=0.2×10×0.9×0.5 J=0.9 J.
变式3 (2016·全国卷Ⅱ·24)如图6,水平面(纸面)内间距为l的平行金属导轨间接一电阻,质量为m、长度为l的金属杆置于导轨上.t=0时,金属杆在水平向右、大小为F的恒定拉力作用下由静止开始运动.t0时刻,金属杆进入磁感应强度大小为B、方向垂直于纸面向里的匀强磁场区域,且在磁场中恰好能保持匀速运动.杆与导轨的电阻均忽略不计,两者始终保持垂直且接触良好,两者之间的动摩擦因数为μ.重力加速度大小为g.求:
图6
(1)金属杆在磁场中运动时产生的电动势的大小;
(2)电阻的阻值.
答案 (1)Blt0(-μg) (2)
解析 (1)设金属杆进入磁场前的加速度大小为a,由牛顿第二定律得F-μmg=ma①
设金属杆到达磁场左边界时的速度为v,由运动学公式有v=at0②
当金属杆以速度v在磁场中运动时,由法拉第电磁感应定律知产生的电动势为E=Blv③
联立①②③式可得
E=Blt0(-μg)④
(2)设金属杆在磁场区域中匀速运动时,金属杆中的电流为I,根据欧姆定律
I=⑤
式中R为电阻的阻值.金属杆所受的安培力为
F安=BlI⑥
因金属杆做匀速运动,有F-μmg-F安=0⑦
联立④⑤⑥⑦式得R=.
1.题型简述
电磁感应过程的实质是不同形式的能量转化的过程,而能量的转化是通过安培力做功来实现的.安培力做功的过程,是电能转化为其他形式的能的过程;外力克服安培力做功的过程,则是其他形式的能转化为电能的过程.
2.解题步骤
(1)确定研究对象(导体棒或回路);
(2)弄清电磁感应过程中,哪些力做功,哪些形式的能量相互转化;
(3)根据能量守恒定律或功能关系列式求解.
3.两类情况
(1)若回路中电流恒定,可以利用电路结构及W=UIt或Q=I2Rt直接进行计算.
(2)若电流变化,则
①利用安培力做功求解:电磁感应中产生的电能等于克服安培力所做的功;
②利用能量守恒求解:若只有电能与机械能的转化,则减少的机械能等于产生的电能.
例4 (2019·北京卷·22)如图7所示,垂直于纸面的匀强磁场磁感应强度为B.纸面内有一正方形均匀金属线框abcd,其边长为L,总电阻为R,ad边与磁场边界平行.从ad边刚进入磁场直至bc边刚要进入的过程中,线框在向左的拉力作用下以速度v匀速运动,求:
图7
(1)感应电动势的大小E;
(2)拉力做功的功率P;
(3)ab边产生的焦耳热Q.
答案 (1)BLv (2) (3)
解析 (1)由法拉第电磁感应定律可得,感应电动势
E=BLv
(2)线框中的感应电流I=
拉力大小等于安培力大小F=BIL
拉力的功率P=Fv=
(3)线框ab边电阻Rab=
时间t=
ab边产生的焦耳热Q=I2Rabt=.
变式4 (2020·宁夏银川市高三质检)如图8所示,水平放置的U形导轨足够长,置于方向竖直向上的匀强磁场中,磁感应强度大小为B=5 T,导轨宽度L=0.4 m,左侧与R=0.5 Ω的定值电阻连接,右侧有导体棒ab垂直导轨跨放在导轨上,导体棒ab质量m=2.0 kg,电阻r=0.5 Ω,与导轨间的动摩擦因数μ=0.2,其余电阻可忽略不计.导体棒ab在大小为10 N的水平外力F作用下,由静止开始运动了x=40 cm后,速度达到最大,取g=10 m/s2.求:
图8
(1)导体棒ab运动的最大速度的大小;
(2)当导体棒ab的速度v=1 m/s时,导体棒ab的加速度的大小;
(3)导体棒ab由静止运动到刚达到最大速度的过程中,电阻R上产生的热量.
答案 (1)1.5 m/s (2)1 m/s2 (3)0.075 J
解析 (1)导体棒ab垂直切割磁感线,产生的感应电动势大小:E=BLv
由闭合电路欧姆定律得:I=
可得导体棒受到的安培力:F安=BIL=
当导体棒做匀速直线运动时速度最大,由平衡条件得:+μmg=F
解得最大速度:vm=1.5 m/s;
(2)当导体棒ab的速度v=1 m/s时,由牛顿第二定律得:F--μmg=ma
解得:a=1 m/s2;
(3)导体棒ab由静止运动到刚达到最大速度的过程中,由能量守恒定律可得:Fx=Q+μmgx+mvm2
解得:Q=0.15 J
所以QR=Q=0.075 J.
