2020年高二数学人教A版选修2-3:分步乘法计数原理 课件(共21张PPT)
文档属性
| 名称 | 2020年高二数学人教A版选修2-3:分步乘法计数原理 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 742.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
分步乘法计数原理
高二年级 数 学
分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法.那么完成这件事共有 种不同的方法.
N=m+n
每类中的任一 种方法都能独立完成这件事情.
两类不同方案中的方法互不相同.
问题1:要从甲、乙、丙不同的画中选出2幅,分别挂在左、右两边的墙上的指定位置,共有多少种不同的挂法?
左边
甲
乙
丙
右边
乙
丙
甲
丙
甲
乙
每一类都有2种方法完成这件事
所以,共有2+2+2=2×3=6种
完成一件事情
“从3幅画中选出2幅,将2幅画分别挂在左右墙上”
问题1:要从甲、乙、丙不同的画中选出2幅,分别挂在左、右两边的墙上的指定位置,共有多少种不同的挂法?
每一类都有2种方法完成这件事
所以,共有2+2+2=2×3=6种
完成一件事情
从3幅画中选出2幅
第1步:
2幅画分别挂在左右墙上
第2步:
未完成这件事
完成这件事用了两步
第1步:3种
第2步:2种
共有3×2=6种
“从3幅画中选出2幅,将2幅画分别挂在左右墙上”
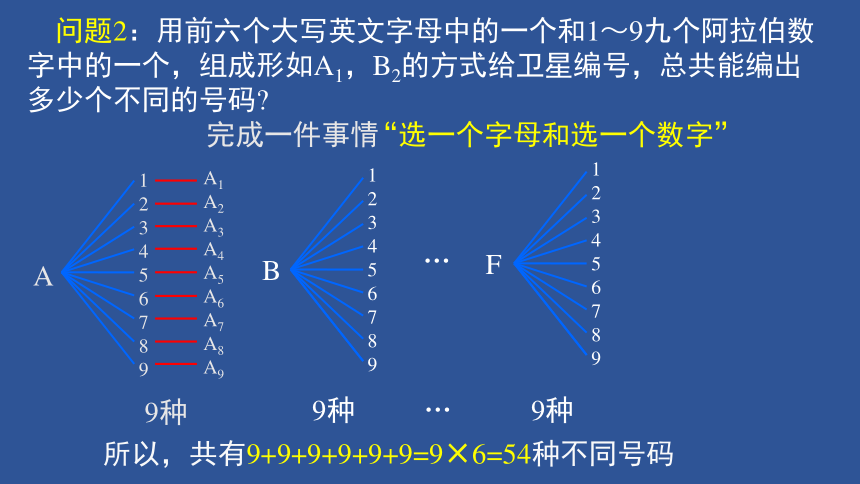
问题2:用前六个大写英文字母中的一个和1~9九个阿拉伯数字中的一个,组成形如A1,B2的方式给卫星编号,总共能编出多少个不同的号码?
B
1
2
3
4
5
6
7
8
9
9种
所以,共有9+9+9+9+9+9=9×6=54种不同号码
F
1
2
3
4
5
6
7
8
9
9种
…
…
完成一件事情
“选一个字母和选一个数字”
A
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
9种
问题2:用前六个大写英文字母中的一个和1~9九个阿拉伯数字中的一个,组成形如A1,B2的方式给卫星编号,总共能编出多少个不同的号码?
所以,共有9+9+9+9+9+9=9×6=54种不同号码
每一类都9种方法完成这件事
完成一件事情
“选一个字母和一个数字”
选一个字母
第1步:
未完成这件事
第1步:6种
选一个数字
第2步:
第2步:9种
完成这件事用了两步
共有6×9=54种
归纳:以上两个问题中“乘法”计数的共同特点
是什么?
问题1 问题2
完成一
件事情
第1步:从3幅画中选出2幅.
第2步:把2幅画分别挂在 左右两边的墙上.
第1步:从前6个大写字母中选一个.
第2步:从1~9九个数字中选一个.
完成一件事有两步
每步中的任一种方法能否独立完成这件事情.
不能
第1步有3种方法
第2步有2种方法
第1步有6种方法
第2步有9种方法
两个步骤互不影响
选一个字母和选一个数字给卫星编号.
从3幅画中选出2幅,把2幅画分别挂在左右墙上.
总共有
3×2=6
6×9=54
分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有
种不同的方法.
每一步中的任一 种方法都不能独立完成这件事情.
两个步骤之间互不影响.
问题3:设某班有男生30名,女生24名.现要从中选出男、女各一名代表班级参加比赛,共有多少种不同的选法?
问:若该班有10名任课老师,要从中选派1名老师作领队,组成代表队,共有多少种不同选法?
解:第一步,从30名男生中选出1名,有30种不同选择;
=7200
30
×
24
×
10
=720
完成一件事情
“选男、女各一名”
第二步,从24名女生中选出1名,有24种不同选择.
和“选任课教师一名”
第三步,从10名老师中选出1名,有10种不同选择.
30
×
24
如果完成一件事需要三个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,做第3步有m3种不同的方法,那么完成这件事共有
种不同的方法.
N=m1×m2×m3
如果完成一件事需要n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
种不同的方法.
N=m1×m2×…×mn
分步乘法计数原理
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架第1,2,3层各取1本书,有多少种不同取法?
练1
完成一件事情
“第1,2,3层各取1本书”
第1层拿出一本计算机书
第2层拿出一本文艺书
第3层拿出一本体育书
未完成
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架第1,2,3层各取1本书,有多少种不同取法?
练1
完成一件事情
“第1,2,3层各取1本书”
第1层拿出一本计算机书
第2层拿出一本文艺书
第3层拿出一本体育书
4种
3种
2种
一共有4×3×2=24 种
完成一件事有3个步骤
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
练1
(2)从书架中任取1本书,有多少种不同取法?
完成一件事情
“从任何一层取1本书”
第1层拿出一本计算机书
完成
第2层拿出一本文艺书
第3层拿出一本体育书
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
练1
(2)从书架中任取1本书,有多少种不同取法?
完成一件事情
“从任何一层取1本书”
第1层拿出一本计算机书
完成一件事有3类方案
第2层拿出一本文艺书
第3层拿出一本体育书
4种
3种
2种
一共有4+3+2=9 种
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(2)从书架中任取1本书,有多少种不同取法?
共有N=4+3+2=9种.
(1)从书架第1,2,3层各取1本书,有多少种不同取法?
共有N=4×3×2=24种.
练1
弄清完成一件事情的要求至关重要,只有这样才能正确区分“分类”和“分步”
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
练1
(3)从书架中取2本不同种类的书,有多少种不同的取法?
完成一件事情
“从书架中取2本不同种类的书”
完成一件事情
取计算机书和文艺书
取计算机书和体育书
取体育书和文艺书
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
练1
(3)从书架中取2本不同种类的书,有多少种不同的取法?
完成一件事情
“从书架中取2本不同种类的书”
完成一件事情
取计算机书和文艺书
取计算机书和体育书
取体育书和文艺书
1步:取计算机书
2步:取文艺书
4×3=12
2步:取文艺书
2步:取体育书
1步:取计算机书
1步:取体育书
4×2=8
2×3=6
12+8+6=26(种)
分步法计数原理
完成一件事
第1步
第n步
····
步与步之间互不影响
完成一件事情需要n步
m1种
m2种
mn种
每一步下的任何一种方法都不能独立完成这件事.
步骤完整
第2步
N=m1×m2×…×mn
小结:
1.解决计数问题的基本方法:
2.选择两个原理解题的关键是:
根据题目,弄清完成一件事的要求至关重要,只有这样才能正确区分“分类”和“分步”.
列举法—探寻方向
分类法—不重不漏
分步法—步骤完整
课后作业
(1)10页 1,2,3,4
(2)12页—A组
分步乘法计数原理
高二年级 数 学
分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法.那么完成这件事共有 种不同的方法.
N=m+n
每类中的任一 种方法都能独立完成这件事情.
两类不同方案中的方法互不相同.
问题1:要从甲、乙、丙不同的画中选出2幅,分别挂在左、右两边的墙上的指定位置,共有多少种不同的挂法?
左边
甲
乙
丙
右边
乙
丙
甲
丙
甲
乙
每一类都有2种方法完成这件事
所以,共有2+2+2=2×3=6种
完成一件事情
“从3幅画中选出2幅,将2幅画分别挂在左右墙上”
问题1:要从甲、乙、丙不同的画中选出2幅,分别挂在左、右两边的墙上的指定位置,共有多少种不同的挂法?
每一类都有2种方法完成这件事
所以,共有2+2+2=2×3=6种
完成一件事情
从3幅画中选出2幅
第1步:
2幅画分别挂在左右墙上
第2步:
未完成这件事
完成这件事用了两步
第1步:3种
第2步:2种
共有3×2=6种
“从3幅画中选出2幅,将2幅画分别挂在左右墙上”
问题2:用前六个大写英文字母中的一个和1~9九个阿拉伯数字中的一个,组成形如A1,B2的方式给卫星编号,总共能编出多少个不同的号码?
B
1
2
3
4
5
6
7
8
9
9种
所以,共有9+9+9+9+9+9=9×6=54种不同号码
F
1
2
3
4
5
6
7
8
9
9种
…
…
完成一件事情
“选一个字母和选一个数字”
A
1
2
3
4
5
6
7
8
9
A1
A2
A3
A4
A5
A6
A7
A8
A9
9种
问题2:用前六个大写英文字母中的一个和1~9九个阿拉伯数字中的一个,组成形如A1,B2的方式给卫星编号,总共能编出多少个不同的号码?
所以,共有9+9+9+9+9+9=9×6=54种不同号码
每一类都9种方法完成这件事
完成一件事情
“选一个字母和一个数字”
选一个字母
第1步:
未完成这件事
第1步:6种
选一个数字
第2步:
第2步:9种
完成这件事用了两步
共有6×9=54种
归纳:以上两个问题中“乘法”计数的共同特点
是什么?
问题1 问题2
完成一
件事情
第1步:从3幅画中选出2幅.
第2步:把2幅画分别挂在 左右两边的墙上.
第1步:从前6个大写字母中选一个.
第2步:从1~9九个数字中选一个.
完成一件事有两步
每步中的任一种方法能否独立完成这件事情.
不能
第1步有3种方法
第2步有2种方法
第1步有6种方法
第2步有9种方法
两个步骤互不影响
选一个字母和选一个数字给卫星编号.
从3幅画中选出2幅,把2幅画分别挂在左右墙上.
总共有
3×2=6
6×9=54
分步乘法计数原理
完成一件事需要两个步骤,做第1步有m种不同的方法,做第2步有n种不同的方法,那么完成这件事共有
种不同的方法.
每一步中的任一 种方法都不能独立完成这件事情.
两个步骤之间互不影响.
问题3:设某班有男生30名,女生24名.现要从中选出男、女各一名代表班级参加比赛,共有多少种不同的选法?
问:若该班有10名任课老师,要从中选派1名老师作领队,组成代表队,共有多少种不同选法?
解:第一步,从30名男生中选出1名,有30种不同选择;
=7200
30
×
24
×
10
=720
完成一件事情
“选男、女各一名”
第二步,从24名女生中选出1名,有24种不同选择.
和“选任课教师一名”
第三步,从10名老师中选出1名,有10种不同选择.
30
×
24
如果完成一件事需要三个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,做第3步有m3种不同的方法,那么完成这件事共有
种不同的方法.
N=m1×m2×m3
如果完成一件事需要n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有
种不同的方法.
N=m1×m2×…×mn
分步乘法计数原理
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架第1,2,3层各取1本书,有多少种不同取法?
练1
完成一件事情
“第1,2,3层各取1本书”
第1层拿出一本计算机书
第2层拿出一本文艺书
第3层拿出一本体育书
未完成
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(1)从书架第1,2,3层各取1本书,有多少种不同取法?
练1
完成一件事情
“第1,2,3层各取1本书”
第1层拿出一本计算机书
第2层拿出一本文艺书
第3层拿出一本体育书
4种
3种
2种
一共有4×3×2=24 种
完成一件事有3个步骤
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
练1
(2)从书架中任取1本书,有多少种不同取法?
完成一件事情
“从任何一层取1本书”
第1层拿出一本计算机书
完成
第2层拿出一本文艺书
第3层拿出一本体育书
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
练1
(2)从书架中任取1本书,有多少种不同取法?
完成一件事情
“从任何一层取1本书”
第1层拿出一本计算机书
完成一件事有3类方案
第2层拿出一本文艺书
第3层拿出一本体育书
4种
3种
2种
一共有4+3+2=9 种
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
(2)从书架中任取1本书,有多少种不同取法?
共有N=4+3+2=9种.
(1)从书架第1,2,3层各取1本书,有多少种不同取法?
共有N=4×3×2=24种.
练1
弄清完成一件事情的要求至关重要,只有这样才能正确区分“分类”和“分步”
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
练1
(3)从书架中取2本不同种类的书,有多少种不同的取法?
完成一件事情
“从书架中取2本不同种类的书”
完成一件事情
取计算机书和文艺书
取计算机书和体育书
取体育书和文艺书
书架第1层放有4本不同的计算机书,第2层放有3本不同的文艺书,第3层放有2本不同的体育书.
练1
(3)从书架中取2本不同种类的书,有多少种不同的取法?
完成一件事情
“从书架中取2本不同种类的书”
完成一件事情
取计算机书和文艺书
取计算机书和体育书
取体育书和文艺书
1步:取计算机书
2步:取文艺书
4×3=12
2步:取文艺书
2步:取体育书
1步:取计算机书
1步:取体育书
4×2=8
2×3=6
12+8+6=26(种)
分步法计数原理
完成一件事
第1步
第n步
····
步与步之间互不影响
完成一件事情需要n步
m1种
m2种
mn种
每一步下的任何一种方法都不能独立完成这件事.
步骤完整
第2步
N=m1×m2×…×mn
小结:
1.解决计数问题的基本方法:
2.选择两个原理解题的关键是:
根据题目,弄清完成一件事的要求至关重要,只有这样才能正确区分“分类”和“分步”.
列举法—探寻方向
分类法—不重不漏
分步法—步骤完整
课后作业
(1)10页 1,2,3,4
(2)12页—A组
