2020年高二数学人教A版选修2-3:分类加法计数原理 课件(共18张PPT)
文档属性
| 名称 | 2020年高二数学人教A版选修2-3:分类加法计数原理 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 562.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
分类加法计数原理
高二年级 数 学
日常生活、生产中有很多计数的问题存在,例如:
(1)班际篮球赛,一定赛制下,共需要举行多少场比赛?
(2)汽车牌照号,一定要求下,可以有多少种排列方式?
(3)核糖核酸分子,碱基数量一定下,会组成多少种RNA?
问题1:能被5整除的两位数有多少个?
方法一:
10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95
方法二:
个位是0的两位数:9个
个位是5的两位数:9个
一共有18个
则9+9=18(个)
问题2:填写高考志愿表时,一名高中毕业生了解到,A ,B两所大学各有一些自己感兴趣的强项专业,具体如下:
A大学
生物学
化学
医学
物理学
工程学
B大学
数学
会计学
信息技术学
法学
问:如果这名同学只能选一个专业,那么他共有多少种选择呢?
方法一:生物学,化学,医学,物理学,工程学,数学,会计学,信息技术学,法学. 一共9种
方法二:A大学中有5种专业
则:5+4=9(种)
B大学中有4种专业
归纳:方法二在计数方面有什么共同特点?
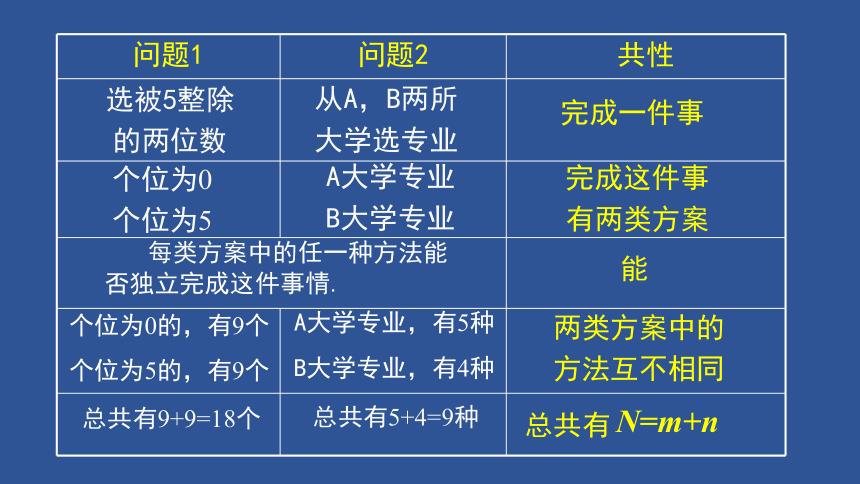
问题1 问题2 共性
每类方案中的任一种方法能否独立完成这件事情.
个位为0的,有9个
个位为5的,有9个
A大学专业,有5种
B大学专业,有4种
完成一件事
完成这件事
有两类方案
能
个位为0
个位为5
A大学专业
B大学专业
总共有9+9=18个
总共有5+4=9种
两类方案中的方法互不相同
选被5整除
的两位数
从A,B两所
大学选专业
总共有
N=m+n
分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法. 那么完成这件事共有:
种不同的方法.
N=m+n
每类中的任一种方法都能独立完成这件事情.
两类不同方案中的方法互不相同.
问题3:在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,具体如下:
问:如果这名同学只能选一个专业,那么他共有多少种选择呢?
A大学
生物学
化学
医学
物理学
工程学
B大学
数学
会计学
信息技术学
法学
6
4
+
=10
数学
?
因为要确定的是这名同学的专业选择,并不是考虑学校的差异
两类不同方案中的方法互不相同.
6
4
+
=9
-
1
问题4:在填写高考志愿表时,一名高中毕业生了解到,A ,B两所大学各有一些自己感兴趣的强项专业,具体如下:
问:如果这名同学只能选一个专业,那么他共有多少种选择呢?
A大学
生物学
化学
医学
物理学
工程学
B大学
数学
会计学
信息技术学
法学
C大学
新闻学
金融学
人力资源学
·····
5+4+3+m1+m2 +…=N
5+4+3=12
完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有:
种不同的方法.
N=m1+m2+…+mn
分类加法计数原理
完成一件事有三类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,在第3 类方案中有m3种不同的方法,那么完成这件事共有:
种不同的方法.
N=m1+m2+m3
1.一件工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是_______.
要完成“一件事情”是“ ”
不同的选法种数是5+4=9
选出1人完成工作
一类是从只会第1种方法的5人中选出一人
一类是从只会第2种方法的4人中选出一人
2.由电键组A,B,C,所组成的并联电路中,如下图,要接通电源(每次只允许合上一个电键),则使电灯发光的方法有_____种.
要完成“一件事情”是“ ”
闭合一个电键,使电灯发光
不同的方法数是1+2+3=6.
3.在所有的两位数中,个位数字大于十位数字的两位数共有多少个?
完成的是哪一件事?
“组成个位数字大于十位数字的两位数”
解:个位数字是9,则十位数字可以是1,2,3,4,5,6,7,8中
的一个,故有8个;
个位数字是8,则十位数字可以是1,2,3,4,5,6,7中的
一个,故有7个;
….
个位数字是2,则十位数字只可以是1,故有1个.
则一共有1+2+3+4+5+6+7+8=36(个)
4.在1~100的数中,会出现多少个数字6?
你要先确定一个分类标准
解:
第一类:一位数
第二类:两位数
有1个
Ⅱ类:十位是6,个位不是6
Ⅰ类:个位是6,十位不是6
Ⅲ类:十位是6,个位也是6
有8个
有9个
有1个
每类中的任一种方法都能独立完成这件事情
一共有1+8+9+1=19个
5.已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为 ( ) .
A.40 B.16 C.13 D.10
【解析】分两类情况讨论:第1类,直线a分别与直线b上的8个点可以确定8个不同的平面;第2类,直线b分别与直线a上的5个点可以确定5个不同的平面. 根据分类加法计数原理知,共可以确定8+5=13个不同的平面.
教科书第6页练习:
1—(1);2—(1);3
第12页A组—1
课后作业
分类加法计数原理
完成一件事
第1类
第n类
·····
类与类之间互不相容
确定一个分类的标准
m1种
m2种
mn种
任何一种方法都能完成任务
N=m1+m2+…+mn
不重不漏
谢谢再见
分类加法计数原理
高二年级 数 学
日常生活、生产中有很多计数的问题存在,例如:
(1)班际篮球赛,一定赛制下,共需要举行多少场比赛?
(2)汽车牌照号,一定要求下,可以有多少种排列方式?
(3)核糖核酸分子,碱基数量一定下,会组成多少种RNA?
问题1:能被5整除的两位数有多少个?
方法一:
10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95
方法二:
个位是0的两位数:9个
个位是5的两位数:9个
一共有18个
则9+9=18(个)
问题2:填写高考志愿表时,一名高中毕业生了解到,A ,B两所大学各有一些自己感兴趣的强项专业,具体如下:
A大学
生物学
化学
医学
物理学
工程学
B大学
数学
会计学
信息技术学
法学
问:如果这名同学只能选一个专业,那么他共有多少种选择呢?
方法一:生物学,化学,医学,物理学,工程学,数学,会计学,信息技术学,法学. 一共9种
方法二:A大学中有5种专业
则:5+4=9(种)
B大学中有4种专业
归纳:方法二在计数方面有什么共同特点?
问题1 问题2 共性
每类方案中的任一种方法能否独立完成这件事情.
个位为0的,有9个
个位为5的,有9个
A大学专业,有5种
B大学专业,有4种
完成一件事
完成这件事
有两类方案
能
个位为0
个位为5
A大学专业
B大学专业
总共有9+9=18个
总共有5+4=9种
两类方案中的方法互不相同
选被5整除
的两位数
从A,B两所
大学选专业
总共有
N=m+n
分类加法计数原理
完成一件事有两类不同方案,在第1类方案中有m种不同的方法,在第2类方案中有n种不同的方法. 那么完成这件事共有:
种不同的方法.
N=m+n
每类中的任一种方法都能独立完成这件事情.
两类不同方案中的方法互不相同.
问题3:在填写高考志愿表时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,具体如下:
问:如果这名同学只能选一个专业,那么他共有多少种选择呢?
A大学
生物学
化学
医学
物理学
工程学
B大学
数学
会计学
信息技术学
法学
6
4
+
=10
数学
?
因为要确定的是这名同学的专业选择,并不是考虑学校的差异
两类不同方案中的方法互不相同.
6
4
+
=9
-
1
问题4:在填写高考志愿表时,一名高中毕业生了解到,A ,B两所大学各有一些自己感兴趣的强项专业,具体如下:
问:如果这名同学只能选一个专业,那么他共有多少种选择呢?
A大学
生物学
化学
医学
物理学
工程学
B大学
数学
会计学
信息技术学
法学
C大学
新闻学
金融学
人力资源学
·····
5+4+3+m1+m2 +…=N
5+4+3=12
完成一件事有n类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,……,在第n类方案中有mn种不同的方法,那么完成这件事共有:
种不同的方法.
N=m1+m2+…+mn
分类加法计数原理
完成一件事有三类不同方案,在第1类方案中有m1种不同的方法,在第2类方案中有m2种不同的方法,在第3 类方案中有m3种不同的方法,那么完成这件事共有:
种不同的方法.
N=m1+m2+m3
1.一件工作可以用2种方法完成,有5人只会用第1种方法完成,另有4人只会用第2种方法完成,从中选出1人来完成这件工作,不同选法的种数是_______.
要完成“一件事情”是“ ”
不同的选法种数是5+4=9
选出1人完成工作
一类是从只会第1种方法的5人中选出一人
一类是从只会第2种方法的4人中选出一人
2.由电键组A,B,C,所组成的并联电路中,如下图,要接通电源(每次只允许合上一个电键),则使电灯发光的方法有_____种.
要完成“一件事情”是“ ”
闭合一个电键,使电灯发光
不同的方法数是1+2+3=6.
3.在所有的两位数中,个位数字大于十位数字的两位数共有多少个?
完成的是哪一件事?
“组成个位数字大于十位数字的两位数”
解:个位数字是9,则十位数字可以是1,2,3,4,5,6,7,8中
的一个,故有8个;
个位数字是8,则十位数字可以是1,2,3,4,5,6,7中的
一个,故有7个;
….
个位数字是2,则十位数字只可以是1,故有1个.
则一共有1+2+3+4+5+6+7+8=36(个)
4.在1~100的数中,会出现多少个数字6?
你要先确定一个分类标准
解:
第一类:一位数
第二类:两位数
有1个
Ⅱ类:十位是6,个位不是6
Ⅰ类:个位是6,十位不是6
Ⅲ类:十位是6,个位也是6
有8个
有9个
有1个
每类中的任一种方法都能独立完成这件事情
一共有1+8+9+1=19个
5.已知两条异面直线a,b上分别有5个点和8个点,则这13个点可以确定不同的平面个数为 ( ) .
A.40 B.16 C.13 D.10
【解析】分两类情况讨论:第1类,直线a分别与直线b上的8个点可以确定8个不同的平面;第2类,直线b分别与直线a上的5个点可以确定5个不同的平面. 根据分类加法计数原理知,共可以确定8+5=13个不同的平面.
教科书第6页练习:
1—(1);2—(1);3
第12页A组—1
课后作业
分类加法计数原理
完成一件事
第1类
第n类
·····
类与类之间互不相容
确定一个分类的标准
m1种
m2种
mn种
任何一种方法都能完成任务
N=m1+m2+…+mn
不重不漏
谢谢再见
