2020年高二数学人教A版选修2-3:离散型随机变量的均值 课件(共21张PPT)
文档属性
| 名称 | 2020年高二数学人教A版选修2-3:离散型随机变量的均值 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 720.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 09:17:54 | ||
图片预览







文档简介
(共21张PPT)
离散型随机变量的均值
高二年级 数学
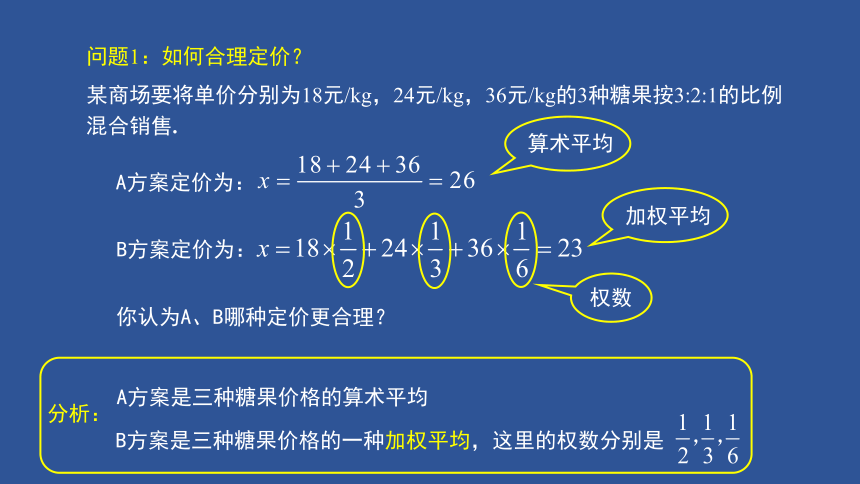
某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售.
问题1:如何合理定价?
A方案定价为:
B方案定价为:
B方案是三种糖果价格的一种加权平均,这里的权数分别是
你认为A、B哪种定价更合理?
A方案是三种糖果价格的算术平均
分析:
算术平均
加权平均
权数
问题2:你能解释权数的含义吗?
如果混合糖果中每颗糖果的质量相等,在混合糖果中,任取一颗糖果.
设X为这颗糖的价格,已知下方为X的分布列:
X 18 24 36
P
分布列中X所对应的概率即为加权平均中每一类X所对应的权数.
B方案更合理:
合理价格
定义:离散型随机变量的均值
(数学期望)
一般地,若离散型随机变量X的概率分布为:
则称:
为随机变量X的均值(或数学期望).
X x1 x2 … xi … xn
P p1 p2 … pi … pn
它反映了离散型随机变量取值的平均水平.
练:随机抛掷一枚质地均匀的骰子,求所得骰子的点数X的期望.
解:随机变量X的取值为1,2,3,4,5,6.
X的分布列为:
变式:若将所得点数的2倍加1作为新得分数Y,即Y=2X+1,试求Y的期望?
X 1 2 3 4 5 6
P
随机变量X的均值为 E(X)= 1× +2× +3× +4× +5× +6× =3.5.
问题1: 我们现在已知 E(X)= 3.5 ,E(Y)= 8 ,Y=2X+1,
变式:若将所得点数的2倍加1作为新得分数Y,即Y=2X+1,试求Y的期望?
Y的分布列为:
E(Y)= 3× +5× +7× +9× +11× +13× =8.
解:
随机变量Y的所有取值为:3,5,7,9,11,13.
Y 3 5 7 9 11 13
P
你能发现E(X),E(Y)之间有什么样的关系吗?
有一定的线性关系: E(Y)= 2E(X)+1=2×3.5+1=8.
期望的线性性质:
若X是一个随机变量,Y=aX+b(a,b是常数),则Y也是一个随机变量,
E(Y)=E(aX+b)=aE(X)+b.
问题1: 我们现在已知E(X)= 3.5,E(Y)= 8 ,Y=2X+1,
你能发现E(X),E(Y)有什么样的关系吗?
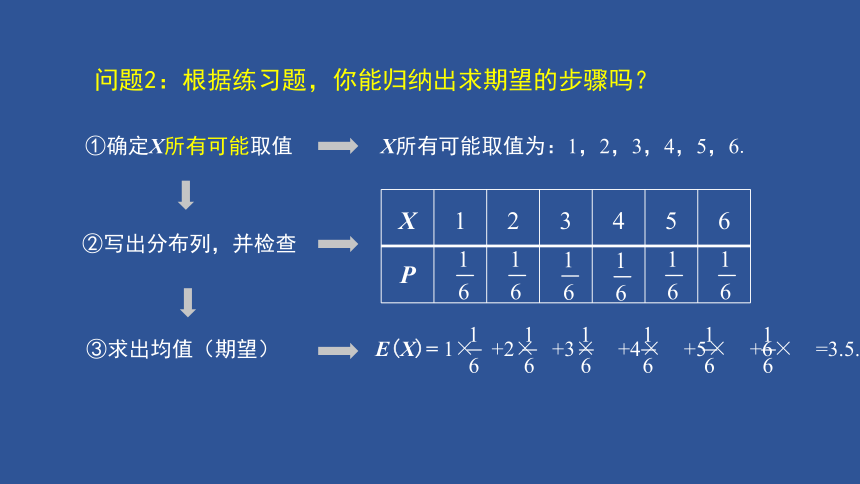
问题2:根据练习题,你能归纳出求期望的步骤吗?
①确定X所有可能取值
②写出分布列,并检查
③求出均值(期望)
X所有可能取值为:1,2,3,4,5,6.
X 1 2 3 4 5 6
P
E(X)= 1× +2× +3× +4× +5× +6× =3.5.
求证:E(Y)=E(aX+b)=aE(X)+b.
X x1 x2 … xi … xn
Y ax1+b ax2+b … axi+b … axn+b
P p1 p2 … pi … pn
问题3:试证明出期望的线性性质
证明:
例1:篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.
已知某运动员罚球命中的概率为0.7.
(1)则他罚球1次的得分X的均值是多少?
(2)他连续罚球3次,求他得到的分数X的期望.
(1)因为 P(X=1)=0.7, P(X=0)=0.3,
解:
所以 E(X)=1×P(X=1)+0×P(X=0)=1×0.7+0×0.3=0.7.
(2)X~B(3,0.7) .
X 0 1 2 3
P 0.33 0.73
特殊分布:X~B(n,p) ,则EX=np
例1:篮球运动员在比赛中每次罚球命中得1分,罚不中得0分
已知某运动员罚球命中的概率为0.7.
(2)他连续罚球3次,求他得到的分数X的期望.
解:
=np
提示:
性质2:特殊分布
1.一般地,如果随机变量X服从两点分布
2.一般地,如果随机变量X服从二项分布,即X~B(n,p)
EX=1×p+0×(1-p)=p
EX=np
练习:一次单元测验由20个选择题构成,每个选择题有4个选项,其中
有且只有一个选项是正确答案,每题选对得5分,不选择或选错
不得分,满分100分.学生甲选对任意一题的概率为0.9,学生乙则
在测验中对每题都从各选项中随机选择一个.求学生甲和乙在这次
测验中的成绩的均值.
解:设学生甲和学生乙在这次单元测验中选对的题数分别是X1和X2,
则X1~B(20,0.9), X2~B(20,0.25).
所以,E(X1) =20×0.9=18,E(X2) =20×0.25=5.
由于每题选对得5分,所以学生甲和学生乙在这次测验中的成绩分别是5X1和5X2,这样,他们在测验中的成绩的期望分别是
E(5X1)=5E(X1)=18×5=90, E(5X2)=5E(X2)=5×5=25.
问题:学生甲在这次测试中的成绩一定会是90分吗?
他的均值为90分的含义是什么?
小结:
随机变量的均值是常数,我们可用它对未发生的事件进行预测.
例2.根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率
为0.01.该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,
遇到小洪水时要损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元;
方案2:建保护围墙,建设费为2000元.但围墙只能防小洪水;
方案3:不采取措施,希望不发生洪水.试比较哪一种方案好?
分析:因为每种情况发生损失都不同,所以比较哪一种方案好,就要
拿损失的均值来比较.
解:设X1,X2,X3分别表示三种方案的损失,
采用第一种方案,无论有无洪水,都损失3800元,即E(X1)=3800.
采用第二种方案,遇到大洪水时,损失2000+60000=62000元,
没有大洪水时,损失2000元,即
采用第三种方案,则
E(X3) =60000×0.01+10000×0.25=3100.
结论:方案2平均损失最小,可以选择方案2.
X2 62000 2000
P 0.01 0.99
E(X2) =62000×0.01+2000×0.99=2600.
X3 0 10000 60000
P 0.74 0.25 0.01
既利用数据分析,又考虑实际情况.
1.随机变量x 的分布列是:
(1)则E x = .
2.4
(2)若h =2x +1,则Eh = .
5.8
x 1 3 5
P 0.5 0.3 0.2
练习:
解:
(期望的线性性质)
2.随机变量x 的分布列是:
Ex =7.5,则a= ,b= .
0.4
0.1
x 4 7 9 10
P 0.3 a b 0.2
解:
解方程组,得:
总结:一个定义、两个性质、一个步骤.
1.离散型随机变量均值(期望)的定义:
2.离散型随机变量均值的性质:
3.归纳求离散型随机变量均值的步骤:
E(aX+b)=aE(X)+b.
①确定X所有可能取值;②写出分布列,并检查;③求出均值.
课后作业:
课本P64练习(2-5),P68习题2.3(2,3,4).
谢谢,再见
离散型随机变量的均值
高二年级 数学
某商场要将单价分别为18元/kg,24元/kg,36元/kg的3种糖果按3:2:1的比例混合销售.
问题1:如何合理定价?
A方案定价为:
B方案定价为:
B方案是三种糖果价格的一种加权平均,这里的权数分别是
你认为A、B哪种定价更合理?
A方案是三种糖果价格的算术平均
分析:
算术平均
加权平均
权数
问题2:你能解释权数的含义吗?
如果混合糖果中每颗糖果的质量相等,在混合糖果中,任取一颗糖果.
设X为这颗糖的价格,已知下方为X的分布列:
X 18 24 36
P
分布列中X所对应的概率即为加权平均中每一类X所对应的权数.
B方案更合理:
合理价格
定义:离散型随机变量的均值
(数学期望)
一般地,若离散型随机变量X的概率分布为:
则称:
为随机变量X的均值(或数学期望).
X x1 x2 … xi … xn
P p1 p2 … pi … pn
它反映了离散型随机变量取值的平均水平.
练:随机抛掷一枚质地均匀的骰子,求所得骰子的点数X的期望.
解:随机变量X的取值为1,2,3,4,5,6.
X的分布列为:
变式:若将所得点数的2倍加1作为新得分数Y,即Y=2X+1,试求Y的期望?
X 1 2 3 4 5 6
P
随机变量X的均值为 E(X)= 1× +2× +3× +4× +5× +6× =3.5.
问题1: 我们现在已知 E(X)= 3.5 ,E(Y)= 8 ,Y=2X+1,
变式:若将所得点数的2倍加1作为新得分数Y,即Y=2X+1,试求Y的期望?
Y的分布列为:
E(Y)= 3× +5× +7× +9× +11× +13× =8.
解:
随机变量Y的所有取值为:3,5,7,9,11,13.
Y 3 5 7 9 11 13
P
你能发现E(X),E(Y)之间有什么样的关系吗?
有一定的线性关系: E(Y)= 2E(X)+1=2×3.5+1=8.
期望的线性性质:
若X是一个随机变量,Y=aX+b(a,b是常数),则Y也是一个随机变量,
E(Y)=E(aX+b)=aE(X)+b.
问题1: 我们现在已知E(X)= 3.5,E(Y)= 8 ,Y=2X+1,
你能发现E(X),E(Y)有什么样的关系吗?
问题2:根据练习题,你能归纳出求期望的步骤吗?
①确定X所有可能取值
②写出分布列,并检查
③求出均值(期望)
X所有可能取值为:1,2,3,4,5,6.
X 1 2 3 4 5 6
P
E(X)= 1× +2× +3× +4× +5× +6× =3.5.
求证:E(Y)=E(aX+b)=aE(X)+b.
X x1 x2 … xi … xn
Y ax1+b ax2+b … axi+b … axn+b
P p1 p2 … pi … pn
问题3:试证明出期望的线性性质
证明:
例1:篮球运动员在比赛中每次罚球命中得1分,罚不中得0分.
已知某运动员罚球命中的概率为0.7.
(1)则他罚球1次的得分X的均值是多少?
(2)他连续罚球3次,求他得到的分数X的期望.
(1)因为 P(X=1)=0.7, P(X=0)=0.3,
解:
所以 E(X)=1×P(X=1)+0×P(X=0)=1×0.7+0×0.3=0.7.
(2)X~B(3,0.7) .
X 0 1 2 3
P 0.33 0.73
特殊分布:X~B(n,p) ,则EX=np
例1:篮球运动员在比赛中每次罚球命中得1分,罚不中得0分
已知某运动员罚球命中的概率为0.7.
(2)他连续罚球3次,求他得到的分数X的期望.
解:
=np
提示:
性质2:特殊分布
1.一般地,如果随机变量X服从两点分布
2.一般地,如果随机变量X服从二项分布,即X~B(n,p)
EX=1×p+0×(1-p)=p
EX=np
练习:一次单元测验由20个选择题构成,每个选择题有4个选项,其中
有且只有一个选项是正确答案,每题选对得5分,不选择或选错
不得分,满分100分.学生甲选对任意一题的概率为0.9,学生乙则
在测验中对每题都从各选项中随机选择一个.求学生甲和乙在这次
测验中的成绩的均值.
解:设学生甲和学生乙在这次单元测验中选对的题数分别是X1和X2,
则X1~B(20,0.9), X2~B(20,0.25).
所以,E(X1) =20×0.9=18,E(X2) =20×0.25=5.
由于每题选对得5分,所以学生甲和学生乙在这次测验中的成绩分别是5X1和5X2,这样,他们在测验中的成绩的期望分别是
E(5X1)=5E(X1)=18×5=90, E(5X2)=5E(X2)=5×5=25.
问题:学生甲在这次测试中的成绩一定会是90分吗?
他的均值为90分的含义是什么?
小结:
随机变量的均值是常数,我们可用它对未发生的事件进行预测.
例2.根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率
为0.01.该地区某工地上有一台大型设备,遇到大洪水时要损失60000元,
遇到小洪水时要损失10000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3800元;
方案2:建保护围墙,建设费为2000元.但围墙只能防小洪水;
方案3:不采取措施,希望不发生洪水.试比较哪一种方案好?
分析:因为每种情况发生损失都不同,所以比较哪一种方案好,就要
拿损失的均值来比较.
解:设X1,X2,X3分别表示三种方案的损失,
采用第一种方案,无论有无洪水,都损失3800元,即E(X1)=3800.
采用第二种方案,遇到大洪水时,损失2000+60000=62000元,
没有大洪水时,损失2000元,即
采用第三种方案,则
E(X3) =60000×0.01+10000×0.25=3100.
结论:方案2平均损失最小,可以选择方案2.
X2 62000 2000
P 0.01 0.99
E(X2) =62000×0.01+2000×0.99=2600.
X3 0 10000 60000
P 0.74 0.25 0.01
既利用数据分析,又考虑实际情况.
1.随机变量x 的分布列是:
(1)则E x = .
2.4
(2)若h =2x +1,则Eh = .
5.8
x 1 3 5
P 0.5 0.3 0.2
练习:
解:
(期望的线性性质)
2.随机变量x 的分布列是:
Ex =7.5,则a= ,b= .
0.4
0.1
x 4 7 9 10
P 0.3 a b 0.2
解:
解方程组,得:
总结:一个定义、两个性质、一个步骤.
1.离散型随机变量均值(期望)的定义:
2.离散型随机变量均值的性质:
3.归纳求离散型随机变量均值的步骤:
E(aX+b)=aE(X)+b.
①确定X所有可能取值;②写出分布列,并检查;③求出均值.
课后作业:
课本P64练习(2-5),P68习题2.3(2,3,4).
谢谢,再见
