2020年高二数学人教A版选修2-3:离散型随机变量及其分布列 课件(共23张PPT)
文档属性
| 名称 | 2020年高二数学人教A版选修2-3:离散型随机变量及其分布列 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 669.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 09:20:17 | ||
图片预览







文档简介
(共23张PPT)
离散型随机变量及其分布列
高二年级 数学
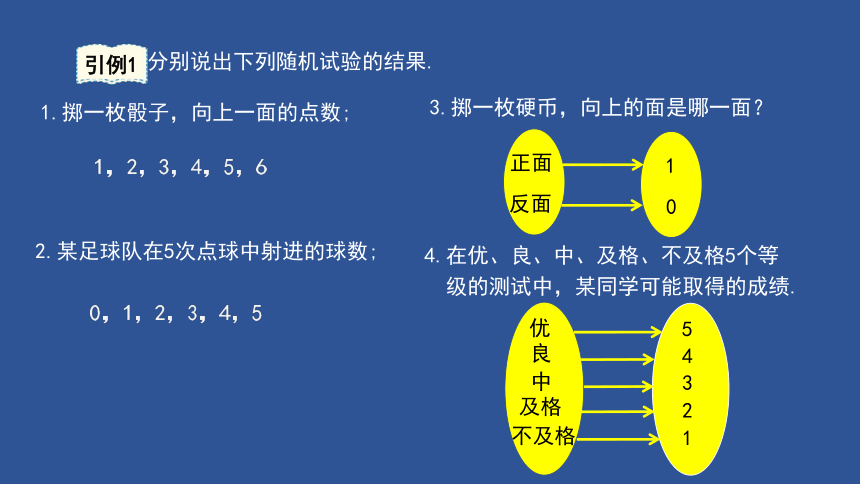
1.掷一枚骰子,向上一面的点数;
2.某足球队在5次点球中射进的球数;
3.掷一枚硬币,向上的面是哪一面?
分别说出下列随机试验的结果.
4.在优、良、中、及格、不及格5个等
级的测试中,某同学可能取得的成绩.
1,2,3,4,5,6
0,1,2,3,4,5
正面
反面
1
0
优
良
中
及格
不及格
5
4
3
2
1
引例1
随着试验结果的变化而变化的变量称为随机变量.
随机变量常用字母 表示.
随机变量
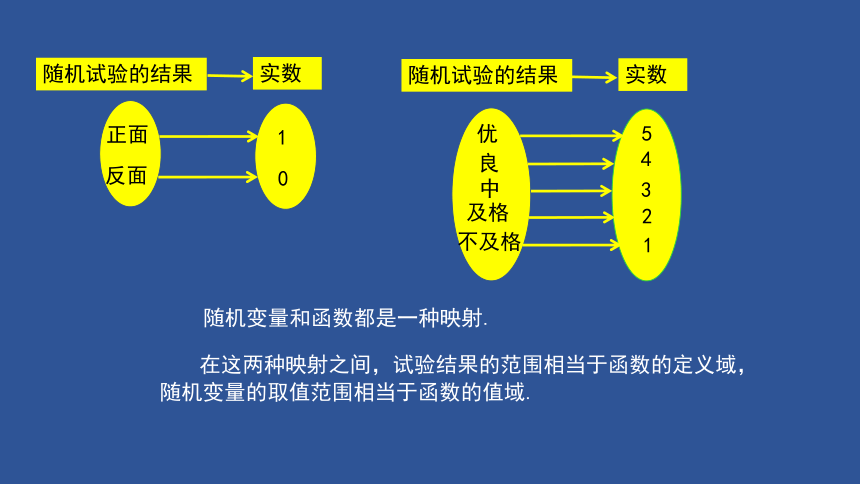
随机试验的结果
实数
随机变量和函数都是一种映射.
在这两种映射之间,试验结果的范围相当于函数的定义域,
随机变量的取值范围相当于函数的值域.
随机试验的结果
实数
正面
反面
1
0
优
良
中
及格
不及格
5
4
3
2
1
袋中有3个白球、5个黑球,从中任取2个,可以作为随机
变量的是( )
A.至少取到1个白球 B.至多取到1个白球
C.取到白球的个数 D.取到的球的个数
例题引申:在上题中,设取到白球的个数为X ,你能说出
表示什么事件吗?取出的白球个数不超过1又该如何用X 表示?
表示取出1个白球;
C
例
请说出下列随机试验中随机变量可能的取值.
1.某人射击一次可能命中的环数.
2.在含有10件次品的100件产品中,任意抽取4件,可能含有的次品件数.
3.某网页在24小时内被浏览的次数.
0,1,2,3,4,5,6,7,8,9,10
0,1,2,3,4
0,1,2,3,……
所有取值可以一一列出的随机变量,称为离散型随机变量.
引例2
问题1:电灯泡的寿命X 是随机变量吗?
问题2:电灯泡的寿命X 是离散型随机变量吗?
问题3:定义如下随机变量:
Y 是离散型随机变量吗?
答案:是
答案:不是
答案:是
请回答下面的问题.
练习
下列随机试验的结果能否用离散型随机变量表示?
若能,请写出各随机变量可能的取值.
1.抛掷两枚骰子,所得点数之和.
能用离散型随机变量表示;
可能的取值有:2,3,4,5,6,7,8,9,10,11,12.
2.一个袋子中装有5个白球和5个黑球,从中任取3个,所含白球的个数.
能用离散型随机变量表示;可能的取值有:0,1,2,3.
3.某一自动装置无故障运转的时间.
不能用离散型随机变量来表示.
练习
下列变量中,不是离散型随机变量的是 ( )
练习
A.从5张已编号的卡片(从1号到5号)中任取一张,
被取出的号数;
B.连续不断射击,首次命中目标所需要的射击次数;
C.某工厂加工的某种钢管内径与规定的内径尺寸之差;
D.电话号码“110”每分钟被呼叫的次数.
C
掷一枚质地均匀的骰子,用X 表示骰子向上一面的点数.
2
1
X
3
4
5
6
P
引例3
一般地,若离散型随机变量X 可能取的不同值为
X 取每一个值
的概率
,以表格的形式表示
如下:
将这个表称为离散型随机变量X 的概率分布列,简称为X 的分
布列.有时为了方便起见,也用等式
表示X 的分布列.
离散型随机变量的分布列
1.分布列中,随机变量的各个可能值表示的事件是彼此互斥的;
注意:
2.求离散型随机变量分布列的“三步曲”:
第一步:写出离散型随机变量的所有可能取值;
第二步:求出离散型随机变量相应的概率值;
第三步:写出离散型随机变量的分布列.
和函数一样,离散型随机变量的分布列除了用表格,或解析式
表示,还可以用图象表示.
在掷骰子试验中,掷出的点数X 的分布列在直角坐标系中的图象
如图所示.
X
P
0.1
0.2
1
3
4
5
6
2
O
离散型随机变量的分布列具有如下性质:
注意:
在写出随机变量的分布列后,要及时检查所有的
概率之和是否等于1.若求出的分布列不满足这条性质,
则说明计算过程中存在错误.
袋中装有 2个白球和 4个黑球,现有甲、乙两人从袋中轮流
摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人
中有一人取到黑球时终止, 每个球在每一次被取出的机会是等可能
的,用X 表示取球终止时所需要的取球次数,求随机变量X 的分布列.
解:由题意得,X 的可能取值为 1,2,3.
X 1 2 3
P
因此,随机变量X 的分布列为
例
判断下列结论的正误.
(1)离散型随机变量的分布列中,随机变量各个取值对应
的概率之和可以小于1. ( )
(2)离散型随机变量的各个可能值表示的事件是彼此互斥
的. ( )
√
练习
设随机变量X 的分布列如下:
X 1 2 3 4 5
P
则实数 p 的取值为 ( )
A. B. C. D.
C
分析:由概率分布列的性质可知,
练习
若离散型随机变量X 的概率分布列为:
X -1 0 2
P
则实数 .
分析:由概率分布列的性质可知,
解得 ,或
(舍).
练习
设随机变量X 的分布列如下表.若随机变量
练习
则 .
X 0 1 2 3 4
P 0.2 0.1 0.1 0.3 m
A. 0.2 B. 0.3 C. 0.4 D. 0.5
分析:由概率分布列的性质,可得
.由
因此
所以
,得 或
D
已知随机变量X 的分布列为:
则(1) ( );
(2) ( ).
(2)分析:
练习
抛掷一枚质地均匀的硬币2次,写出正面向上次数X 的
分布列.
解:由题意得,X 的可能取值为 0,1,2.
X 0 1 2
P
因此,随机变量X 的分布列为
练习
课堂小结:
离散型随机变量的分布列及性质
离散型随机变量
随机变量
教材第49页第1、2、3、4、5题
课后作业:
离散型随机变量及其分布列
高二年级 数学
1.掷一枚骰子,向上一面的点数;
2.某足球队在5次点球中射进的球数;
3.掷一枚硬币,向上的面是哪一面?
分别说出下列随机试验的结果.
4.在优、良、中、及格、不及格5个等
级的测试中,某同学可能取得的成绩.
1,2,3,4,5,6
0,1,2,3,4,5
正面
反面
1
0
优
良
中
及格
不及格
5
4
3
2
1
引例1
随着试验结果的变化而变化的变量称为随机变量.
随机变量常用字母 表示.
随机变量
随机试验的结果
实数
随机变量和函数都是一种映射.
在这两种映射之间,试验结果的范围相当于函数的定义域,
随机变量的取值范围相当于函数的值域.
随机试验的结果
实数
正面
反面
1
0
优
良
中
及格
不及格
5
4
3
2
1
袋中有3个白球、5个黑球,从中任取2个,可以作为随机
变量的是( )
A.至少取到1个白球 B.至多取到1个白球
C.取到白球的个数 D.取到的球的个数
例题引申:在上题中,设取到白球的个数为X ,你能说出
表示什么事件吗?取出的白球个数不超过1又该如何用X 表示?
表示取出1个白球;
C
例
请说出下列随机试验中随机变量可能的取值.
1.某人射击一次可能命中的环数.
2.在含有10件次品的100件产品中,任意抽取4件,可能含有的次品件数.
3.某网页在24小时内被浏览的次数.
0,1,2,3,4,5,6,7,8,9,10
0,1,2,3,4
0,1,2,3,……
所有取值可以一一列出的随机变量,称为离散型随机变量.
引例2
问题1:电灯泡的寿命X 是随机变量吗?
问题2:电灯泡的寿命X 是离散型随机变量吗?
问题3:定义如下随机变量:
Y 是离散型随机变量吗?
答案:是
答案:不是
答案:是
请回答下面的问题.
练习
下列随机试验的结果能否用离散型随机变量表示?
若能,请写出各随机变量可能的取值.
1.抛掷两枚骰子,所得点数之和.
能用离散型随机变量表示;
可能的取值有:2,3,4,5,6,7,8,9,10,11,12.
2.一个袋子中装有5个白球和5个黑球,从中任取3个,所含白球的个数.
能用离散型随机变量表示;可能的取值有:0,1,2,3.
3.某一自动装置无故障运转的时间.
不能用离散型随机变量来表示.
练习
下列变量中,不是离散型随机变量的是 ( )
练习
A.从5张已编号的卡片(从1号到5号)中任取一张,
被取出的号数;
B.连续不断射击,首次命中目标所需要的射击次数;
C.某工厂加工的某种钢管内径与规定的内径尺寸之差;
D.电话号码“110”每分钟被呼叫的次数.
C
掷一枚质地均匀的骰子,用X 表示骰子向上一面的点数.
2
1
X
3
4
5
6
P
引例3
一般地,若离散型随机变量X 可能取的不同值为
X 取每一个值
的概率
,以表格的形式表示
如下:
将这个表称为离散型随机变量X 的概率分布列,简称为X 的分
布列.有时为了方便起见,也用等式
表示X 的分布列.
离散型随机变量的分布列
1.分布列中,随机变量的各个可能值表示的事件是彼此互斥的;
注意:
2.求离散型随机变量分布列的“三步曲”:
第一步:写出离散型随机变量的所有可能取值;
第二步:求出离散型随机变量相应的概率值;
第三步:写出离散型随机变量的分布列.
和函数一样,离散型随机变量的分布列除了用表格,或解析式
表示,还可以用图象表示.
在掷骰子试验中,掷出的点数X 的分布列在直角坐标系中的图象
如图所示.
X
P
0.1
0.2
1
3
4
5
6
2
O
离散型随机变量的分布列具有如下性质:
注意:
在写出随机变量的分布列后,要及时检查所有的
概率之和是否等于1.若求出的分布列不满足这条性质,
则说明计算过程中存在错误.
袋中装有 2个白球和 4个黑球,现有甲、乙两人从袋中轮流
摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人
中有一人取到黑球时终止, 每个球在每一次被取出的机会是等可能
的,用X 表示取球终止时所需要的取球次数,求随机变量X 的分布列.
解:由题意得,X 的可能取值为 1,2,3.
X 1 2 3
P
因此,随机变量X 的分布列为
例
判断下列结论的正误.
(1)离散型随机变量的分布列中,随机变量各个取值对应
的概率之和可以小于1. ( )
(2)离散型随机变量的各个可能值表示的事件是彼此互斥
的. ( )
√
练习
设随机变量X 的分布列如下:
X 1 2 3 4 5
P
则实数 p 的取值为 ( )
A. B. C. D.
C
分析:由概率分布列的性质可知,
练习
若离散型随机变量X 的概率分布列为:
X -1 0 2
P
则实数 .
分析:由概率分布列的性质可知,
解得 ,或
(舍).
练习
设随机变量X 的分布列如下表.若随机变量
练习
则 .
X 0 1 2 3 4
P 0.2 0.1 0.1 0.3 m
A. 0.2 B. 0.3 C. 0.4 D. 0.5
分析:由概率分布列的性质,可得
.由
因此
所以
,得 或
D
已知随机变量X 的分布列为:
则(1) ( );
(2) ( ).
(2)分析:
练习
抛掷一枚质地均匀的硬币2次,写出正面向上次数X 的
分布列.
解:由题意得,X 的可能取值为 0,1,2.
X 0 1 2
P
因此,随机变量X 的分布列为
练习
课堂小结:
离散型随机变量的分布列及性质
离散型随机变量
随机变量
教材第49页第1、2、3、4、5题
课后作业:
