2020年高二数学人教A版选修2-3:探究与发现-组合数的两个性质 课件(共21张PPT)
文档属性
| 名称 | 2020年高二数学人教A版选修2-3:探究与发现-组合数的两个性质 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 871.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览






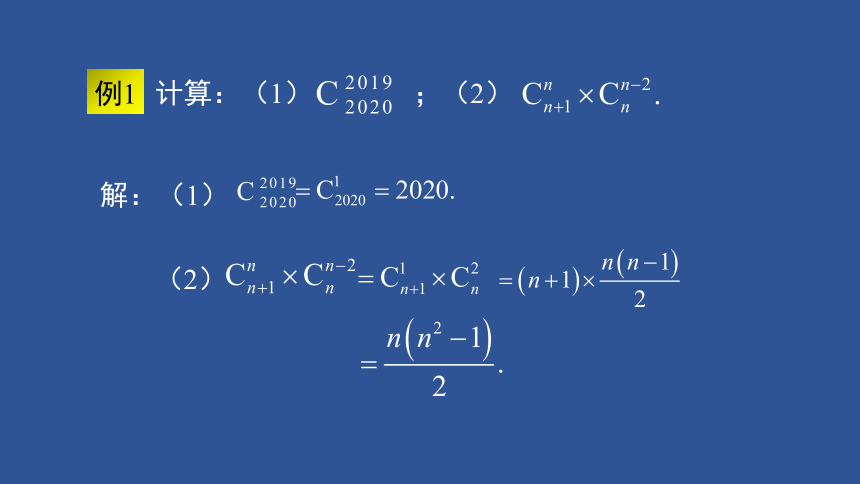


文档简介
(共21张PPT)
高二年级 数学
探究与发现:组合数的两个性质
一、复习与回顾
2.组合数公式:
=
1.组合数 定义:
=
=
你发现了什么?你能解释你的发现吗?
=
如何解释上述结果呢?
10名学生中选出3人参加某项活动的选法种数,
10名学生中留下7人不参加活动的选法种数.
从n个不同元素中
取出m个元素
剩下n-m个元素
一一对应
二、组合数的两个性质
②还原为实际问题的解释.
③用公式证明:
性质1
.
① =1, 时也成立.
二、组合数的两个性质
特点:
等式的两边组合数下标相同,
上标的和等于下标.
应用:
简化运算.
性质1
.
解:(1)
例1
计算:(1) ;(2)
(2)
仿照性质1进行证明
还原成实际问题:从7名学生中选4名参加某项活动,
①甲同学未被选中的不同选法种数,
②甲同学被选中的不同选法种数.
用组合数公式证明.
性质2
发现
不含“ ”
含“ ”
计算 , ,
性质2
特点:
等式右边的两个组合数,下标相同,上标差1.
相加后的组合数,下标加1,上标取较大的.
应用:恒等变形,化简计算.
例2
化简
难点:
突破:
解:原式
1.已知 ,那么n
三、随堂练习
6
2.计算
∵ = = = 21,
或
(舍).
3.你能构造一个实际背景,对等式
的意义做出解释吗?
你能构造一个实际背景,对等式
的意义作出解释吗?
按照 分步乘法 计数原理
理解
n名同学
选k名同学进入网络会议打开视频
选m-k名同学进入网络会议
选m名同学进入网络会议
选其中k名同学打开视频
四、巩固提升
1.解关于 的方程
解:
且满足
或
或
下标相等的两个组合数相等的充要条件
是什么?
2.计算
大数化小,由繁化简.
解:
3.求证:
由复杂的一侧入手,转化为化简问题.不妨试一试!
证明:右边
=左边.
得证.
2
2
2
2
2
2
2
2
…
1 2 3 4 5 … n-2 n-1 n
√ √
4.你能构造一个实际背景,
对等式 的意义做出解释吗?
分类加法计数原理
分步乘法
计数原理
小明考试有n道判断题,小明答题所有可能情况有多少?
1 2 3 4 5 … n-2 n-1 n
√×
5.证明下列等式成立:
难点:两侧都比较复杂.
突破1:右侧有 ,左侧没有.
解:左边=
类似
等差数列
前n项和
(1)
(2)
由(1)+(2)得
5.证明下列等式成立:
突破2: .
难点:左侧通项 .
解: 左边 .
实际背景
=右边.
五、课后思考
证明下列等式成立:
类比地学,联系地学,
在具体例子中想到它蕴含的一般概念,
在一般概念中感受到事物的“灵魂”.
祝同学们学习愉快!
高二年级 数学
探究与发现:组合数的两个性质
一、复习与回顾
2.组合数公式:
=
1.组合数 定义:
=
=
你发现了什么?你能解释你的发现吗?
=
如何解释上述结果呢?
10名学生中选出3人参加某项活动的选法种数,
10名学生中留下7人不参加活动的选法种数.
从n个不同元素中
取出m个元素
剩下n-m个元素
一一对应
二、组合数的两个性质
②还原为实际问题的解释.
③用公式证明:
性质1
.
① =1, 时也成立.
二、组合数的两个性质
特点:
等式的两边组合数下标相同,
上标的和等于下标.
应用:
简化运算.
性质1
.
解:(1)
例1
计算:(1) ;(2)
(2)
仿照性质1进行证明
还原成实际问题:从7名学生中选4名参加某项活动,
①甲同学未被选中的不同选法种数,
②甲同学被选中的不同选法种数.
用组合数公式证明.
性质2
发现
不含“ ”
含“ ”
计算 , ,
性质2
特点:
等式右边的两个组合数,下标相同,上标差1.
相加后的组合数,下标加1,上标取较大的.
应用:恒等变形,化简计算.
例2
化简
难点:
突破:
解:原式
1.已知 ,那么n
三、随堂练习
6
2.计算
∵ = = = 21,
或
(舍).
3.你能构造一个实际背景,对等式
的意义做出解释吗?
你能构造一个实际背景,对等式
的意义作出解释吗?
按照 分步乘法 计数原理
理解
n名同学
选k名同学进入网络会议打开视频
选m-k名同学进入网络会议
选m名同学进入网络会议
选其中k名同学打开视频
四、巩固提升
1.解关于 的方程
解:
且满足
或
或
下标相等的两个组合数相等的充要条件
是什么?
2.计算
大数化小,由繁化简.
解:
3.求证:
由复杂的一侧入手,转化为化简问题.不妨试一试!
证明:右边
=左边.
得证.
2
2
2
2
2
2
2
2
…
1 2 3 4 5 … n-2 n-1 n
√ √
4.你能构造一个实际背景,
对等式 的意义做出解释吗?
分类加法计数原理
分步乘法
计数原理
小明考试有n道判断题,小明答题所有可能情况有多少?
1 2 3 4 5 … n-2 n-1 n
√×
5.证明下列等式成立:
难点:两侧都比较复杂.
突破1:右侧有 ,左侧没有.
解:左边=
类似
等差数列
前n项和
(1)
(2)
由(1)+(2)得
5.证明下列等式成立:
突破2: .
难点:左侧通项 .
解: 左边 .
实际背景
=右边.
五、课后思考
证明下列等式成立:
类比地学,联系地学,
在具体例子中想到它蕴含的一般概念,
在一般概念中感受到事物的“灵魂”.
祝同学们学习愉快!
