2020年高二数学人教A版选修2-3:正态分布 课件(共32张PPT)
文档属性
| 名称 | 2020年高二数学人教A版选修2-3:正态分布 课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览






文档简介
(共32张PPT)
2.4 正 态 分 布
高二年级 数学
复习导入
一 前两节学习的内容:
平均水平
2. 离散型随机变量 的方差和标准差都反映了随机变量取值偏离于均值的平均程度,方差或标准差越小,则随机变量偏离于均值的平均程度越小.
1. 离散型随机变量 的均值或数学期望,它反映了离散型
随机变量取值的 .
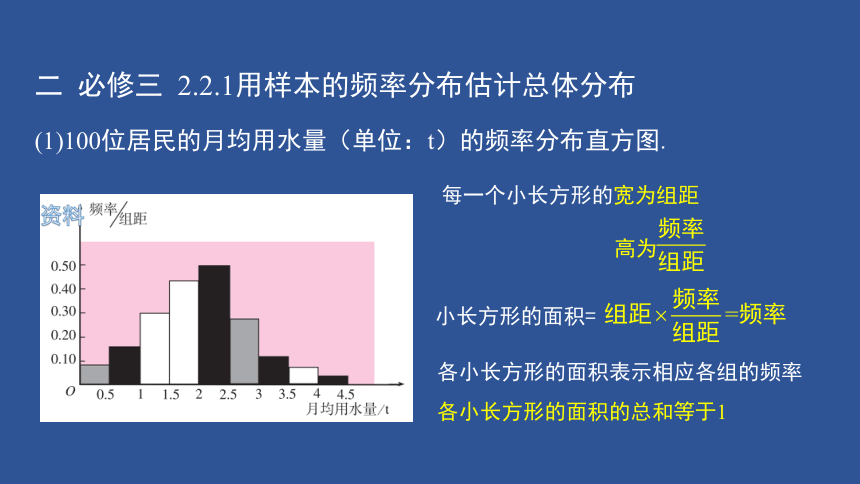
每一个小长方形的宽为组距
各小长方形的面积表示相应各组的频率
各小长方形的面积的总和等于1
二 必修三 2.2.1用样本的频率分布估计总体分布
(1)100位居民的月均用水量(单位:t)的频率分布直方图.
资料
高为
小长方形的面积=
(2) 频率分布折线图
连接频率分布直方图中各小长方形上端的中点,就得到频率分布折线图.
当样本容量增加时
组数增加
组距减小
资料
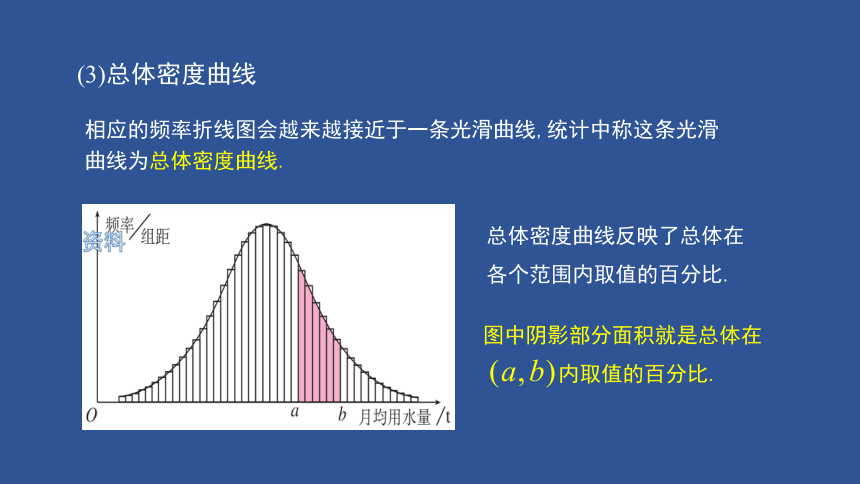
(3)总体密度曲线
相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.
总体密度曲线反映了总体在
各个范围内取值的百分比.
图中阴影部分面积就是总体在
内取值的百分比.
资料
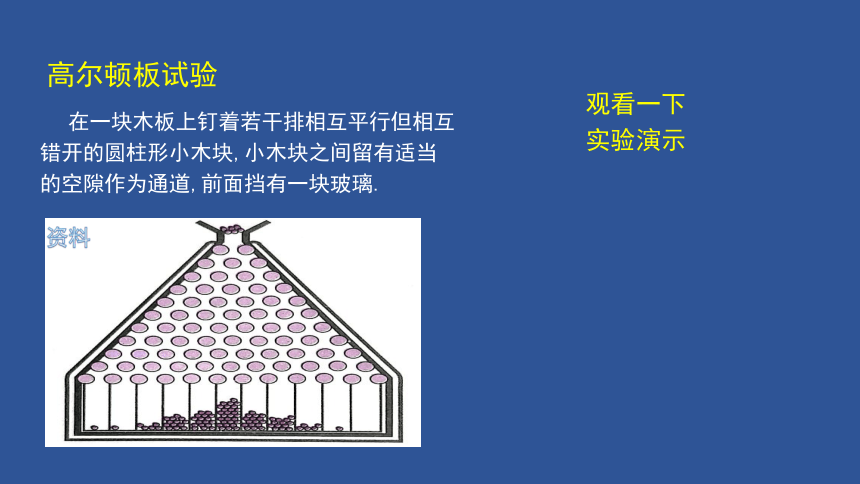
高尔顿板试验
在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.
观看一下
实验演示
资料
天津市春季学期中小学精品课程资源
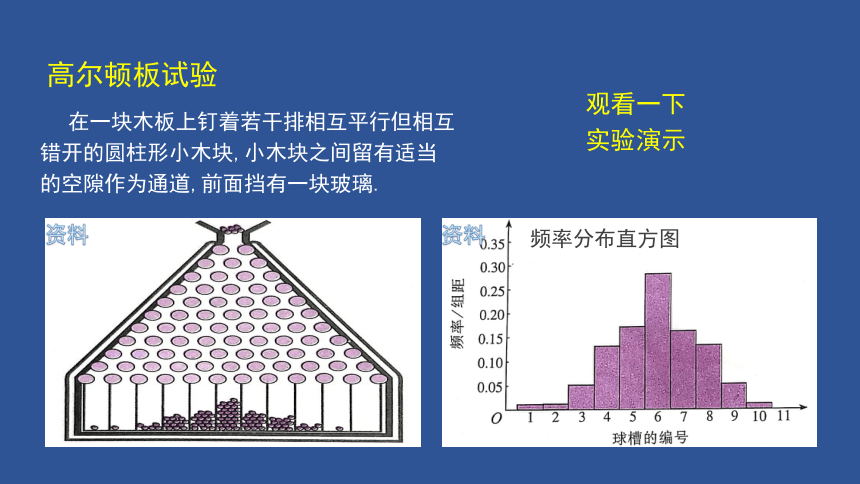
高尔顿板试验
在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.
观看一下
实验演示
资料
频率分布直方图
资料
像一条钟形曲线
总体密度曲线
随着重复次数的增加
该曲线两头无限延伸,且与 轴无限接近但不相交
资料
中间高,两边低,左右对称
简称正态曲线
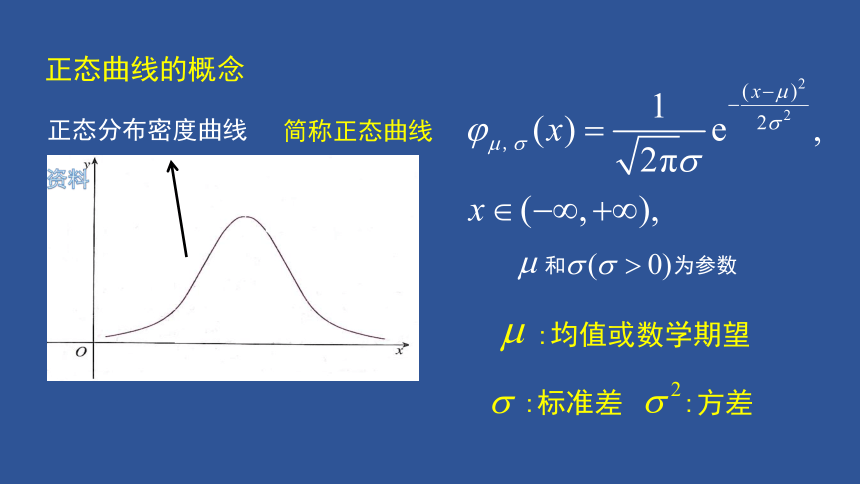
正态曲线的概念
:标准差
:方差
:均值或数学期望
和 为参数
资料
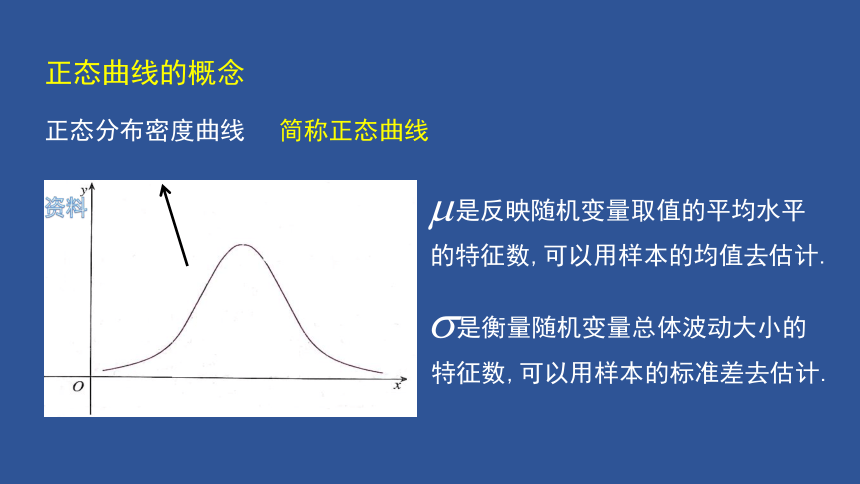
正态分布密度曲线
简称正态曲线
正态分布密度曲线
是反映随机变量取值的平均水平
的特征数,可以用样本的均值去估计.
是衡量随机变量总体波动大小的
特征数,可以用样本的标准差去估计.
正态曲线的概念
资料
如何求 落在区间 的概率?
面积等于频率
就是 落在区间
概率的近似值
资料
则随机变量 服从正态分布.
如果 服从正态分布
,则记为
一般地,如果对于任何实数 和 随机
变量 满足 ,
正态分布完全由参数 和 确定.
经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.
因此小球第1次与高尔顿板底
部接触时的坐标 是众多随机碰
撞的结果,
所以它近似服从正态分布.
如高尔顿板试验中
资料
资料
早在1733年,法国数学家棣莫弗(A.de Moivre,1667-1754)
就用n!的近似公式得到了正态分布.
资料
棣莫弗
之后,德国数学家高斯(C.F.Gause,1777-1855)在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布.
高斯
资料
2.一定条件下生长的小麦
株高
穗长
单位面积产量
零件的尺寸
3.正常生产条件下
各种产品的质量指标
纤维的纤度
电容器的电容量
电子管的使用寿命等
4.某地每年七月份
平均气温
平均湿度
降雨量等
在现实生活中
遗传基因、饮食习惯、
每天锻炼身体的时间等
随机变量
服从或近似服从
正态分布
体重
1.长度测量的误差
某一地区同年龄人群
身高
肺活量
例如
正态曲线的特点
资料
上方
面积为1
观察一下动态
的函数图象
和 为参数
具有以下特点:
(4)曲线与 轴之间的 .
(2)曲线是单峰的,它关于直线 对称;
(3)曲线在 处达到峰值 ;
(1)曲线位于 轴 ,与 轴不相交;
资料
(5)当 一定时,曲线的位置由 确定 ,
曲线随着 的变化而沿着 轴平移;
(6)当 一定时,曲线的形状由 确定,
越小,曲线越“瘦高”,表示总体的分布越集中;
越大,曲线越“矮胖”,表示总体的分布越分散.
资料
3 原则
图中阴影部分的面积
资料
观看一下动态演示
对于固定的 和 而言,
该面积会有什么样的变化呢?
3 原则
图中阴影部分的面积
该面积随着 的减少而变大
这说明 越小,
落在区间 的概率
越大,即 集中在 周围概率越大.
资料
观看一下动态演示
对于固定的 和 而言,
特别有
三个特殊区间的概率
68.27%
95.45%
99.73%
资料
68.27%
95.45%
99.73%
资料
可以看到,正态总体几乎总取值于区间 之内,而在此区间以外取值的概率只有0.0027,通常认为这种情况在一次试验中几乎不可能发生.
一般概率不超过5%
通常称为小概率事件
在实践应用中,通常认为服从于正态分布 的随
机变量 只取 之间的值,并简称之为3 原则.
68.27%
95.45%
99.73%
资料
2.4正态分布
1.正态分布密度曲线
简称正态曲线
是下列函数图象
为均值或数学期望
为标准差
为方差
平均水平
总体波动大小
服从正态分布,则记为
和 为参数
资料
2.正态曲线的特点
2.4正态分布
(3) 曲线在 处达到峰值 ;
(4) 曲线与 轴之间的面积为1.
(2) 曲线是单峰的,它关于直线 对称;
(1) 曲线在 轴上方,与 轴不相交;
(5) 当 一定时,曲线的位置由 确定,曲线随着 的变化
而沿着 轴平移;
(6) 当 一定时,曲线的形状由 确定,
越小,曲线越“瘦高”,表示总体的分布越集中;
越大,曲线越“矮胖”,表示总体的分布越分散.
三个特殊区间的概率
3.3 原则
2.4正态分布
在实践应用中,通常认为服从于正态分布 的随
机变量 只取 之间的值,并简称之为3 原则.
3. 3 原则
(1) 轴上方 不相交
(6) 一定, 越小 “瘦高” 集中
越大 “矮胖” 分散
2.正态曲线的特点
(3) 处 峰值
(4) 轴之间的面积为1
(5) 一定,沿着 轴平移
2.4正态分布
1.正态分布密度曲线
简称正态曲线
是下列函数图象
记为
为均值或数学期望
为标准差
为方差
平均水平
总体波动大小
服从正态分布,则
(2) 单峰的 对称
和 为参数
解:如图,在 处达到峰值 i
(3)曲线在 处达到峰值 ;
由正态曲线特点
可知,
资料
某地区数学考试的成绩 服从正态分布,其密度曲线如图
所示,成绩 位于区间(52,68]的概率是多少?
练习:
课后作业
1. 熟读本节知识导图.
2. 教科书第74页练习3,
第77页B组第2题和第4题.
谢谢大家的聆听!
祝大家身体健康,学习进步!
2.4 正 态 分 布
高二年级 数学
复习导入
一 前两节学习的内容:
平均水平
2. 离散型随机变量 的方差和标准差都反映了随机变量取值偏离于均值的平均程度,方差或标准差越小,则随机变量偏离于均值的平均程度越小.
1. 离散型随机变量 的均值或数学期望,它反映了离散型
随机变量取值的 .
每一个小长方形的宽为组距
各小长方形的面积表示相应各组的频率
各小长方形的面积的总和等于1
二 必修三 2.2.1用样本的频率分布估计总体分布
(1)100位居民的月均用水量(单位:t)的频率分布直方图.
资料
高为
小长方形的面积=
(2) 频率分布折线图
连接频率分布直方图中各小长方形上端的中点,就得到频率分布折线图.
当样本容量增加时
组数增加
组距减小
资料
(3)总体密度曲线
相应的频率折线图会越来越接近于一条光滑曲线,统计中称这条光滑曲线为总体密度曲线.
总体密度曲线反映了总体在
各个范围内取值的百分比.
图中阴影部分面积就是总体在
内取值的百分比.
资料
高尔顿板试验
在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.
观看一下
实验演示
资料
天津市春季学期中小学精品课程资源
高尔顿板试验
在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.
观看一下
实验演示
资料
频率分布直方图
资料
像一条钟形曲线
总体密度曲线
随着重复次数的增加
该曲线两头无限延伸,且与 轴无限接近但不相交
资料
中间高,两边低,左右对称
简称正态曲线
正态曲线的概念
:标准差
:方差
:均值或数学期望
和 为参数
资料
正态分布密度曲线
简称正态曲线
正态分布密度曲线
是反映随机变量取值的平均水平
的特征数,可以用样本的均值去估计.
是衡量随机变量总体波动大小的
特征数,可以用样本的标准差去估计.
正态曲线的概念
资料
如何求 落在区间 的概率?
面积等于频率
就是 落在区间
概率的近似值
资料
则随机变量 服从正态分布.
如果 服从正态分布
,则记为
一般地,如果对于任何实数 和 随机
变量 满足 ,
正态分布完全由参数 和 确定.
经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.
因此小球第1次与高尔顿板底
部接触时的坐标 是众多随机碰
撞的结果,
所以它近似服从正态分布.
如高尔顿板试验中
资料
资料
早在1733年,法国数学家棣莫弗(A.de Moivre,1667-1754)
就用n!的近似公式得到了正态分布.
资料
棣莫弗
之后,德国数学家高斯(C.F.Gause,1777-1855)在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布.
高斯
资料
2.一定条件下生长的小麦
株高
穗长
单位面积产量
零件的尺寸
3.正常生产条件下
各种产品的质量指标
纤维的纤度
电容器的电容量
电子管的使用寿命等
4.某地每年七月份
平均气温
平均湿度
降雨量等
在现实生活中
遗传基因、饮食习惯、
每天锻炼身体的时间等
随机变量
服从或近似服从
正态分布
体重
1.长度测量的误差
某一地区同年龄人群
身高
肺活量
例如
正态曲线的特点
资料
上方
面积为1
观察一下动态
的函数图象
和 为参数
具有以下特点:
(4)曲线与 轴之间的 .
(2)曲线是单峰的,它关于直线 对称;
(3)曲线在 处达到峰值 ;
(1)曲线位于 轴 ,与 轴不相交;
资料
(5)当 一定时,曲线的位置由 确定 ,
曲线随着 的变化而沿着 轴平移;
(6)当 一定时,曲线的形状由 确定,
越小,曲线越“瘦高”,表示总体的分布越集中;
越大,曲线越“矮胖”,表示总体的分布越分散.
资料
3 原则
图中阴影部分的面积
资料
观看一下动态演示
对于固定的 和 而言,
该面积会有什么样的变化呢?
3 原则
图中阴影部分的面积
该面积随着 的减少而变大
这说明 越小,
落在区间 的概率
越大,即 集中在 周围概率越大.
资料
观看一下动态演示
对于固定的 和 而言,
特别有
三个特殊区间的概率
68.27%
95.45%
99.73%
资料
68.27%
95.45%
99.73%
资料
可以看到,正态总体几乎总取值于区间 之内,而在此区间以外取值的概率只有0.0027,通常认为这种情况在一次试验中几乎不可能发生.
一般概率不超过5%
通常称为小概率事件
在实践应用中,通常认为服从于正态分布 的随
机变量 只取 之间的值,并简称之为3 原则.
68.27%
95.45%
99.73%
资料
2.4正态分布
1.正态分布密度曲线
简称正态曲线
是下列函数图象
为均值或数学期望
为标准差
为方差
平均水平
总体波动大小
服从正态分布,则记为
和 为参数
资料
2.正态曲线的特点
2.4正态分布
(3) 曲线在 处达到峰值 ;
(4) 曲线与 轴之间的面积为1.
(2) 曲线是单峰的,它关于直线 对称;
(1) 曲线在 轴上方,与 轴不相交;
(5) 当 一定时,曲线的位置由 确定,曲线随着 的变化
而沿着 轴平移;
(6) 当 一定时,曲线的形状由 确定,
越小,曲线越“瘦高”,表示总体的分布越集中;
越大,曲线越“矮胖”,表示总体的分布越分散.
三个特殊区间的概率
3.3 原则
2.4正态分布
在实践应用中,通常认为服从于正态分布 的随
机变量 只取 之间的值,并简称之为3 原则.
3. 3 原则
(1) 轴上方 不相交
(6) 一定, 越小 “瘦高” 集中
越大 “矮胖” 分散
2.正态曲线的特点
(3) 处 峰值
(4) 轴之间的面积为1
(5) 一定,沿着 轴平移
2.4正态分布
1.正态分布密度曲线
简称正态曲线
是下列函数图象
记为
为均值或数学期望
为标准差
为方差
平均水平
总体波动大小
服从正态分布,则
(2) 单峰的 对称
和 为参数
解:如图,在 处达到峰值 i
(3)曲线在 处达到峰值 ;
由正态曲线特点
可知,
资料
某地区数学考试的成绩 服从正态分布,其密度曲线如图
所示,成绩 位于区间(52,68]的概率是多少?
练习:
课后作业
1. 熟读本节知识导图.
2. 教科书第74页练习3,
第77页B组第2题和第4题.
谢谢大家的聆听!
祝大家身体健康,学习进步!
