人教版七年级数学下册6.3实数第1课时课件(共22张PPT)
文档属性
| 名称 | 人教版七年级数学下册6.3实数第1课时课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 353.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-21 20:40:41 | ||
图片预览








文档简介
(共22张PPT)
人教版初中数学七年级下册第六章 实数
6.3 实数
第1课时 实数及其分类
1.理解无理数和实数的概念,会将实数按一定的标准进行分类.
2.知道实数与数轴上的点一一对应.
学习目标
重点:正确理解实数的概念.
难点:对“实数与数轴上的点一一对应关系”的理解.
重点 难点
1、无限不循环的小数叫做无理数.
2、 有理数和无理数统称实数
3、实数的分类
按定义分类:
有理数
无理数
正有理数
负有理数
0
正有理数
负有理数
有限小数或无限循环小数
无限不循环小数
实数
按性质分类:
正实数
负实数
0
正有理数
负有理数
负有理数
负无理数
实数
4、实数与数轴上点的关系
实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点表示;反过来,数轴上的每一个点都表示一个实数.
1、 对有理数和无理数进行区分时,应先对某些数进行计
算或化简,然后根据最后结果进行分类,不能仅看到
用根号表示的数就认为是无理数.
2、 π是无理数,化简后含π的数也是无理数.
1. 定义:无限不循环小数叫做无理数.
判断标准:小数位数无限,小数形式为不循环.
2. 三种常见形式:
(1)开方开不尽的数,如 ,3 ,…;
(2)含有π的一类数: 9 π, π,π+1,…;
(3)类似0.101 001 000 1…(每相邻两个1之间依次多1个0)
这样的无限不循环小数.
知识点一 无理数
例1:下列说法正确的是( )
A.无理数包括正无理数、0和负无理数
B.无理数是用根号形式表示的数
C.无理数是开方开不尽的数
D.无理数是无限不循环小数
D
无理数
正有理数
负有理数
无限不循环小数
1、下列各数中为无理数的是( )
A.-1 B.3.14
C.π D.0
2、下列说法正确的是( )
A.无限小数是无理数
B.任何分数都是有理数
C. 一定表示无理数
D.π-3.14是有理数
C
B
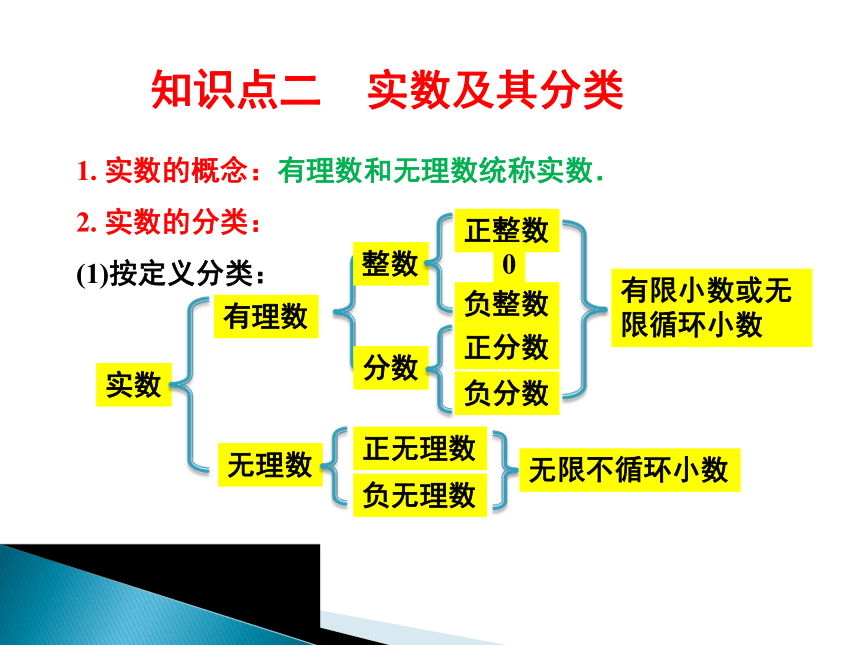
知识点二 实数及其分类
1. 实数的概念:有理数和无理数统称实数.
2. 实数的分类:
(1)按定义分类:
实数
有理数
无理数
整数
分数
正整数
负整数
0
负分数
正分数
正无理数
负无理数
无限不循环小数
有限小数或无限循环小数
1.下列实数中,为有理数的是( )
B.π
C. D.1
2.下列说法正确的是( )
A.正实数和负实数统称实数
B.正数、零和负数统称有理数
C.带根号的数和分数统称实数
D.无理数和有理数统称实数
D
D
3.下列说法中正确的有( )
①无理数都是实数;②实数都是无理数;③无限小数都是有理数;④带根号的数都是无理数;⑤除了π之外不带根号的数都是有理数.
A.1个 B.2个 C.3个 D.4个
由实数定义可知①是正确的;②错误,因为实数不都是无理数,还有有理数;③错误,无限不循环小数是无理数;④错误,如 就是有理数;⑤错误,如0.1010010001…(每两个1之间依次多一个0)就是无理数,所以正确的有1个.
A
4、把下列各数分别填在相应的集合内:
整数集合{ …}; 分数集合{ …};
正数集合{ …}; 负数集合{ …};
有理数集合{ …}; 无理数集合{ …}.
整数集合{ …};
分数集合{ …};
正数集合{ …};
负数集合{ …};
有理数集合{ …};
无理数集合{ …}.
知识点三 实数与数轴上点的关系
实数与数轴间的关系:实数和数轴上的点是一一对应的.
两层含义
(1)每一个实数都可以用数轴上的一个点来表示;
(2)数轴上的每一个点都表示一个实数.
平面直角坐标系中的点与有序实数对 是一一对应的.
数轴上两点间的距离的求法:
数轴上两点间的距离等于表示这两点的数之
差的绝对值.
1、和数轴上的点一一对应的数是( )
A.整数 B.有理数
C.无理数 D.实数
D
3、下列说法正确的是( )
A. 是分数 B. 是分数
C. 分数 D. 0是分数
A
3、如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将该圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
A.π-1 B.-π-1
C.-π+1 D.π-1或-π-1
D
议一议
你能在坐标轴上找到 对应的点吗?与同伴进 行交流.
4、点A在数轴上表示的数为 ,点B在数轴上表示的数为-5,则A,B两点之间的距离为 ________.
根据数轴上两点间的距离等于右边的点表示的数减去左边的点表示的数,列式计算即可得解.
拓展训练
1.a,b是两个连续整数,若
<b,
则a+b的值是( )
A.7 B.9 C.21 D.25
A
∴a=3,b=4,
∴a+b=7
2.实数a,b在数轴上对应的点的位置如图所示,那么
化简的结果( )
A.2a+b B.b C.2a﹣b D.3b
0
b
a
C
a﹣b+a+b﹣b=2a﹣b,
阅读下面的文字,解答问题
大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用 来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:
即
的整数部分为2,小数部分为
(1) 的整数部分是 ,小数部分是
7
(2)如果 的小数部分为a, 的整数部分为b,求|a﹣b|+ 的值.
人教版初中数学七年级下册第六章 实数
6.3 实数
第1课时 实数及其分类
1.理解无理数和实数的概念,会将实数按一定的标准进行分类.
2.知道实数与数轴上的点一一对应.
学习目标
重点:正确理解实数的概念.
难点:对“实数与数轴上的点一一对应关系”的理解.
重点 难点
1、无限不循环的小数叫做无理数.
2、 有理数和无理数统称实数
3、实数的分类
按定义分类:
有理数
无理数
正有理数
负有理数
0
正有理数
负有理数
有限小数或无限循环小数
无限不循环小数
实数
按性质分类:
正实数
负实数
0
正有理数
负有理数
负有理数
负无理数
实数
4、实数与数轴上点的关系
实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点表示;反过来,数轴上的每一个点都表示一个实数.
1、 对有理数和无理数进行区分时,应先对某些数进行计
算或化简,然后根据最后结果进行分类,不能仅看到
用根号表示的数就认为是无理数.
2、 π是无理数,化简后含π的数也是无理数.
1. 定义:无限不循环小数叫做无理数.
判断标准:小数位数无限,小数形式为不循环.
2. 三种常见形式:
(1)开方开不尽的数,如 ,3 ,…;
(2)含有π的一类数: 9 π, π,π+1,…;
(3)类似0.101 001 000 1…(每相邻两个1之间依次多1个0)
这样的无限不循环小数.
知识点一 无理数
例1:下列说法正确的是( )
A.无理数包括正无理数、0和负无理数
B.无理数是用根号形式表示的数
C.无理数是开方开不尽的数
D.无理数是无限不循环小数
D
无理数
正有理数
负有理数
无限不循环小数
1、下列各数中为无理数的是( )
A.-1 B.3.14
C.π D.0
2、下列说法正确的是( )
A.无限小数是无理数
B.任何分数都是有理数
C. 一定表示无理数
D.π-3.14是有理数
C
B
知识点二 实数及其分类
1. 实数的概念:有理数和无理数统称实数.
2. 实数的分类:
(1)按定义分类:
实数
有理数
无理数
整数
分数
正整数
负整数
0
负分数
正分数
正无理数
负无理数
无限不循环小数
有限小数或无限循环小数
1.下列实数中,为有理数的是( )
B.π
C. D.1
2.下列说法正确的是( )
A.正实数和负实数统称实数
B.正数、零和负数统称有理数
C.带根号的数和分数统称实数
D.无理数和有理数统称实数
D
D
3.下列说法中正确的有( )
①无理数都是实数;②实数都是无理数;③无限小数都是有理数;④带根号的数都是无理数;⑤除了π之外不带根号的数都是有理数.
A.1个 B.2个 C.3个 D.4个
由实数定义可知①是正确的;②错误,因为实数不都是无理数,还有有理数;③错误,无限不循环小数是无理数;④错误,如 就是有理数;⑤错误,如0.1010010001…(每两个1之间依次多一个0)就是无理数,所以正确的有1个.
A
4、把下列各数分别填在相应的集合内:
整数集合{ …}; 分数集合{ …};
正数集合{ …}; 负数集合{ …};
有理数集合{ …}; 无理数集合{ …}.
整数集合{ …};
分数集合{ …};
正数集合{ …};
负数集合{ …};
有理数集合{ …};
无理数集合{ …}.
知识点三 实数与数轴上点的关系
实数与数轴间的关系:实数和数轴上的点是一一对应的.
两层含义
(1)每一个实数都可以用数轴上的一个点来表示;
(2)数轴上的每一个点都表示一个实数.
平面直角坐标系中的点与有序实数对 是一一对应的.
数轴上两点间的距离的求法:
数轴上两点间的距离等于表示这两点的数之
差的绝对值.
1、和数轴上的点一一对应的数是( )
A.整数 B.有理数
C.无理数 D.实数
D
3、下列说法正确的是( )
A. 是分数 B. 是分数
C. 分数 D. 0是分数
A
3、如图,圆的直径为1个单位长度,该圆上的点A与数轴上表示-1的点重合,将该圆沿数轴滚动1周,点A到达点A′的位置,则点A′表示的数是( )
A.π-1 B.-π-1
C.-π+1 D.π-1或-π-1
D
议一议
你能在坐标轴上找到 对应的点吗?与同伴进 行交流.
4、点A在数轴上表示的数为 ,点B在数轴上表示的数为-5,则A,B两点之间的距离为 ________.
根据数轴上两点间的距离等于右边的点表示的数减去左边的点表示的数,列式计算即可得解.
拓展训练
1.a,b是两个连续整数,若
<b,
则a+b的值是( )
A.7 B.9 C.21 D.25
A
∴a=3,b=4,
∴a+b=7
2.实数a,b在数轴上对应的点的位置如图所示,那么
化简的结果( )
A.2a+b B.b C.2a﹣b D.3b
0
b
a
C
a﹣b+a+b﹣b=2a﹣b,
阅读下面的文字,解答问题
大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用 来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:
即
的整数部分为2,小数部分为
(1) 的整数部分是 ,小数部分是
7
(2)如果 的小数部分为a, 的整数部分为b,求|a﹣b|+ 的值.
