高中物理人教新版导学案 必修 第一册 第4章 动力学中三种典型物理模型 Word版含解析
文档属性
| 名称 | 高中物理人教新版导学案 必修 第一册 第4章 动力学中三种典型物理模型 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 243.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-20 18:30:23 | ||
图片预览


文档简介
动力学中三种典型物理模型
专题解读 1.本专题是动力学方法在三类典型模型问题中的应用,其中等时圆模型常在选择题中考查,而滑块—木板模型和传送带模型常以计算题压轴题的形式命题.
2.通过本专题的学习,可以培养同学们的审题能力、建模能力、分析推理能力和规范表达等物理学科素养,针对性的专题强化,通过题型特点和解题方法的分析,能帮助同学们迅速提高解题能力.
3.用到的相关知识有:匀变速直线运动规律、牛顿运动定律、相对运动的有关知识.
1.两种模型(如图1)
图1
2.等时性的证明
设某一条光滑弦与水平方向的夹角为α,圆的直径为d,如图1所示.根据物体沿光滑弦做初速度为零的匀加速直线运动,加速度为a=gsin α,位移为x=dsin α,所以运动时间为t0===.
即沿同一起点或终点的各条光滑弦运动具有等时性,运动时间与弦的倾角、长短无关.
例1 (2019·安徽芜湖市期末)如图2所示,PQ为圆的竖直直径,AQ、BQ、CQ为三个光滑斜面轨道,分别与圆相交于A、B、C三点.现让三个小球(可以看作质点)分别沿着AQ、BQ、CQ轨道自端点由静止滑到Q点,运动的平均速度分别为v1、v2和v3.则有:( )
图2
A.v2>v1>v3
B.v1>v2>v3
C.v3>v1>v2
D.v1>v3>v2
答案 A
解析 设任一斜面的倾角为θ,圆槽直径为d.根据牛顿第二定律得到:a=gsin θ,斜面的长度为x=dsin θ,则由x=at2得t===,可见,物体下滑时间与斜面的倾角无关,则有t1=t2=t3,根据=,因x2>x1>x3 ,可知v2>v1>v3,故选A.
变式1 如图3所示,竖直半圆环中有多条起始于A点的光滑轨道,其中AB通过环心O并保持竖直.一质点分别自A点沿各条轨道下滑,初速度均为零.那么,质点沿各轨道下滑的时间相比较( )
图3
A.无论沿图中哪条轨道下滑,所用的时间均相同
B.质点沿着与AB夹角越大的轨道下滑,时间越短
C.质点沿着轨道AB下滑,时间最短
D.轨道与AB夹角越小(AB除外),质点沿其下滑的时间越短
答案 A
1.水平传送带模型
项目 图示 滑块可能的运动情况
情景1 ①可能一直加速 ②可能先加速后匀速
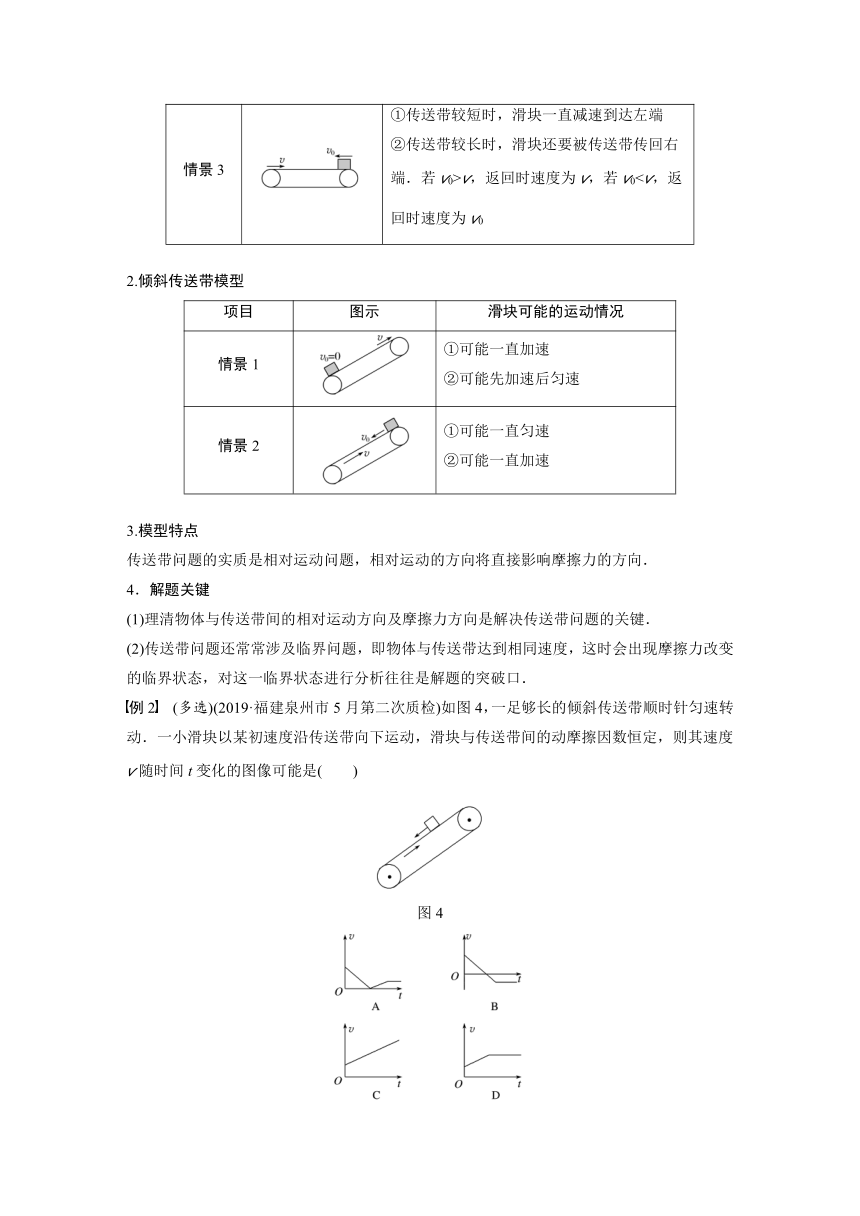
情景2 ①v0>v,可能一直减速,也可能先减速再匀速 ②v0=v,一直匀速 ③v0情景3 ①传送带较短时,滑块一直减速到达左端 ②传送带较长时,滑块还要被传送带传回右端.若v0>v,返回时速度为v,若v02.倾斜传送带模型
项目 图示 滑块可能的运动情况
情景1 ①可能一直加速 ②可能先加速后匀速
情景2 ①可能一直匀速 ②可能一直加速
3.模型特点
传送带问题的实质是相对运动问题,相对运动的方向将直接影响摩擦力的方向.
4.解题关键
(1)理清物体与传送带间的相对运动方向及摩擦力方向是解决传送带问题的关键.
(2)传送带问题还常常涉及临界问题,即物体与传送带达到相同速度,这时会出现摩擦力改变的临界状态,对这一临界状态进行分析往往是解题的突破口.
例2 (多选)(2019·福建泉州市5月第二次质检)如图4,一足够长的倾斜传送带顺时针匀速转动.一小滑块以某初速度沿传送带向下运动,滑块与传送带间的动摩擦因数恒定,则其速度v随时间t变化的图像可能是( )
图4
答案 BC
解析 设传送带倾角为θ,动摩擦因数为μ,若mgsin θ>μmgcos θ,合力沿传送带向下,小滑块向下做匀加速运动;若mgsin θ=μmgcos θ,沿传送带方向合力为零,小滑块匀速下滑;若mgsin θ<μmgcos θ,小滑块所受合力沿传送带向上,小滑块做匀减速运动,当速度减为零时,开始反向加速,当加速到与传送带速度相同时,因为最大静摩擦力大于小滑块重力沿传送带向下的分力,故小滑块随传送带做匀速运动,A、D错误,B、C正确.
变式2 (多选)(2019·陕西榆林市第三次测试)如图5所示,绷紧的水平传送带足够长,且始终以v1=2 m/s的恒定速率顺时针运行.初速度大小为v2=3 m/s的小墨块从与传送带等高的光滑水平地面上的A处滑上传送带.若从小墨块滑上传送带开始计时,小墨块在传送带上运动5 s后与传送带的速度相同,则( )
图5
A.小墨块未与传送带速度相同时,受到的摩擦力方向水平向右
B.小墨块的加速度大小为0.2 m/s2
C.小墨块在传送带上的痕迹长度为4.5 m
D.小墨块在传送带上的痕迹长度为12.5 m
答案 AD
解析 小墨块未与传送带速度相同时,相对传送带向左运动,受到传送带的摩擦力方向水平向右,故A正确.小墨块在摩擦力的作用下做匀变速运动,小墨块在传送带上运动5 s后与传送带的速度相同,故a===1 m/s2,方向向右,故B错误.小墨块向左做匀减速运动时,对小墨块有:0=v2-at1,x1=t1,联立解得:x1=4.5 m,小墨块向左减速的过程中,传送带的位移为:x2=v1t1=6 m;小墨块向右做匀加速运动时,对小墨块有:v1=at2,x1′=t2,联立解得x1′=2 m,对传送带有:x2′=v1t2=4 m,因而小墨块在传送带上的痕迹长度为:x=(x1+x2)+(x2′-x1′)=12.5 m,故C错误,D正确.
1.模型特点
“滑块—木板”模型类问题中,滑动摩擦力的分析方法与“传送带”模型类似,但这类问题比传送带类问题更复杂,因为木板受到摩擦力的影响,往往做匀变速直线运动,解决此类问题要注意从速度、位移、时间等角度,寻找各运动过程之间的联系.
2.解题关键
(1)临界条件:使滑块不从木板的末端掉下来的临界条件是滑块到达木板末端时的速度与木板的速度恰好相同.
(2)问题实质:“板—块”模型和“传送带”模型一样,本质上都是相对运动问题,要分别求出各物体相对地面的位移,再求相对位移.
例3 (2019·贵州毕节市适应性监测(三))一长木板置于粗糙水平地面上,木板右端放置一小物块,如图6所示.木板与地面间的动摩擦因数μ1=0.1,物块与木板间的动摩擦因数μ2=0.4.t=0时刻开始,小物块与木板一起以共同速度向墙壁运动,当t=1 s时,木板以速度v1=4 m/s与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反.运动过程中小物块第一次减速为零时恰好从木板上掉下.已知木板的质量是小物块质量的15倍,重力加速度大小g取10 m/s2.求:
图6
(1)t=0时刻木板的速度大小;
(2)木板的长度.
答案 (1)5 m/s (2) m
解析 (1)对木板和物块:μ1(M+m)g=(M+m)a1
设初始时刻木板速度为v0
由运动学公式:v1=v0-a1t0
代入数据解得:v0=5 m/s
(2)碰撞后,对物块:μ2mg=ma2
对物块,当速度为0时,经历时间t,发生位移x1,则有v1=a2t,x1=t
对木板,由牛顿第二定律:μ2mg+μ1(M+m)g=Ma3
对木板,经历时间t,发生位移x2
x2=v1t-a3t2
木板长度l=x1+x2
联立并代入数据解得l= m.
变式3 (2019·江苏卷·15)如图7所示,质量相等的物块A和B叠放在水平地面上,左边缘对齐.A与B、B与地面间的动摩擦因数均为μ.先敲击A,A立即获得水平向右的初速度,在B上滑动距离L后停下.接着敲击B,B立即获得水平向右的初速度,A、B都向右运动,左边缘再次对齐时恰好相对静止,此后两者一起运动至停下.最大静摩擦力等于滑动摩擦力,重力加速度为g.求:
图7
(1)A被敲击后获得的初速度大小vA;
(2)在左边缘再次对齐的前、后,B运动加速度的大小aB、aB′;
(3)B被敲击后获得的初速度大小vB.
答案 (1) (2)3μg μg (3)2
解析 (1)由牛顿第二定律知,A加速度的大小aA=μg
由匀变速直线运动规律得2aAL=v
解得vA=;
(2)设A、B的质量均为m
对齐前,B所受合外力大小F=3μmg
由牛顿第二定律F=maB,得aB=3μg
对齐后,A、B所受合外力大小F′=2μmg
由牛顿第二定律F′=2maB′,得aB′=μg;
(3)设经过时间t,A、B达到共同速度v,位移分别为xA、xB,A加速度的大小为aA
则v=aAt,v=vB-aBt
xA=aAt2,xB=vBt-aBt2
且xB-xA=L
解得vB=2 .
x2=(24+2-8) m=18 m.
专题解读 1.本专题是动力学方法在三类典型模型问题中的应用,其中等时圆模型常在选择题中考查,而滑块—木板模型和传送带模型常以计算题压轴题的形式命题.
2.通过本专题的学习,可以培养同学们的审题能力、建模能力、分析推理能力和规范表达等物理学科素养,针对性的专题强化,通过题型特点和解题方法的分析,能帮助同学们迅速提高解题能力.
3.用到的相关知识有:匀变速直线运动规律、牛顿运动定律、相对运动的有关知识.
1.两种模型(如图1)
图1
2.等时性的证明
设某一条光滑弦与水平方向的夹角为α,圆的直径为d,如图1所示.根据物体沿光滑弦做初速度为零的匀加速直线运动,加速度为a=gsin α,位移为x=dsin α,所以运动时间为t0===.
即沿同一起点或终点的各条光滑弦运动具有等时性,运动时间与弦的倾角、长短无关.
例1 (2019·安徽芜湖市期末)如图2所示,PQ为圆的竖直直径,AQ、BQ、CQ为三个光滑斜面轨道,分别与圆相交于A、B、C三点.现让三个小球(可以看作质点)分别沿着AQ、BQ、CQ轨道自端点由静止滑到Q点,运动的平均速度分别为v1、v2和v3.则有:( )
图2
A.v2>v1>v3
B.v1>v2>v3
C.v3>v1>v2
D.v1>v3>v2
答案 A
解析 设任一斜面的倾角为θ,圆槽直径为d.根据牛顿第二定律得到:a=gsin θ,斜面的长度为x=dsin θ,则由x=at2得t===,可见,物体下滑时间与斜面的倾角无关,则有t1=t2=t3,根据=,因x2>x1>x3 ,可知v2>v1>v3,故选A.
变式1 如图3所示,竖直半圆环中有多条起始于A点的光滑轨道,其中AB通过环心O并保持竖直.一质点分别自A点沿各条轨道下滑,初速度均为零.那么,质点沿各轨道下滑的时间相比较( )
图3
A.无论沿图中哪条轨道下滑,所用的时间均相同
B.质点沿着与AB夹角越大的轨道下滑,时间越短
C.质点沿着轨道AB下滑,时间最短
D.轨道与AB夹角越小(AB除外),质点沿其下滑的时间越短
答案 A
1.水平传送带模型
项目 图示 滑块可能的运动情况
情景1 ①可能一直加速 ②可能先加速后匀速
情景2 ①v0>v,可能一直减速,也可能先减速再匀速 ②v0=v,一直匀速 ③v0
项目 图示 滑块可能的运动情况
情景1 ①可能一直加速 ②可能先加速后匀速
情景2 ①可能一直匀速 ②可能一直加速
3.模型特点
传送带问题的实质是相对运动问题,相对运动的方向将直接影响摩擦力的方向.
4.解题关键
(1)理清物体与传送带间的相对运动方向及摩擦力方向是解决传送带问题的关键.
(2)传送带问题还常常涉及临界问题,即物体与传送带达到相同速度,这时会出现摩擦力改变的临界状态,对这一临界状态进行分析往往是解题的突破口.
例2 (多选)(2019·福建泉州市5月第二次质检)如图4,一足够长的倾斜传送带顺时针匀速转动.一小滑块以某初速度沿传送带向下运动,滑块与传送带间的动摩擦因数恒定,则其速度v随时间t变化的图像可能是( )
图4
答案 BC
解析 设传送带倾角为θ,动摩擦因数为μ,若mgsin θ>μmgcos θ,合力沿传送带向下,小滑块向下做匀加速运动;若mgsin θ=μmgcos θ,沿传送带方向合力为零,小滑块匀速下滑;若mgsin θ<μmgcos θ,小滑块所受合力沿传送带向上,小滑块做匀减速运动,当速度减为零时,开始反向加速,当加速到与传送带速度相同时,因为最大静摩擦力大于小滑块重力沿传送带向下的分力,故小滑块随传送带做匀速运动,A、D错误,B、C正确.
变式2 (多选)(2019·陕西榆林市第三次测试)如图5所示,绷紧的水平传送带足够长,且始终以v1=2 m/s的恒定速率顺时针运行.初速度大小为v2=3 m/s的小墨块从与传送带等高的光滑水平地面上的A处滑上传送带.若从小墨块滑上传送带开始计时,小墨块在传送带上运动5 s后与传送带的速度相同,则( )
图5
A.小墨块未与传送带速度相同时,受到的摩擦力方向水平向右
B.小墨块的加速度大小为0.2 m/s2
C.小墨块在传送带上的痕迹长度为4.5 m
D.小墨块在传送带上的痕迹长度为12.5 m
答案 AD
解析 小墨块未与传送带速度相同时,相对传送带向左运动,受到传送带的摩擦力方向水平向右,故A正确.小墨块在摩擦力的作用下做匀变速运动,小墨块在传送带上运动5 s后与传送带的速度相同,故a===1 m/s2,方向向右,故B错误.小墨块向左做匀减速运动时,对小墨块有:0=v2-at1,x1=t1,联立解得:x1=4.5 m,小墨块向左减速的过程中,传送带的位移为:x2=v1t1=6 m;小墨块向右做匀加速运动时,对小墨块有:v1=at2,x1′=t2,联立解得x1′=2 m,对传送带有:x2′=v1t2=4 m,因而小墨块在传送带上的痕迹长度为:x=(x1+x2)+(x2′-x1′)=12.5 m,故C错误,D正确.
1.模型特点
“滑块—木板”模型类问题中,滑动摩擦力的分析方法与“传送带”模型类似,但这类问题比传送带类问题更复杂,因为木板受到摩擦力的影响,往往做匀变速直线运动,解决此类问题要注意从速度、位移、时间等角度,寻找各运动过程之间的联系.
2.解题关键
(1)临界条件:使滑块不从木板的末端掉下来的临界条件是滑块到达木板末端时的速度与木板的速度恰好相同.
(2)问题实质:“板—块”模型和“传送带”模型一样,本质上都是相对运动问题,要分别求出各物体相对地面的位移,再求相对位移.
例3 (2019·贵州毕节市适应性监测(三))一长木板置于粗糙水平地面上,木板右端放置一小物块,如图6所示.木板与地面间的动摩擦因数μ1=0.1,物块与木板间的动摩擦因数μ2=0.4.t=0时刻开始,小物块与木板一起以共同速度向墙壁运动,当t=1 s时,木板以速度v1=4 m/s与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反.运动过程中小物块第一次减速为零时恰好从木板上掉下.已知木板的质量是小物块质量的15倍,重力加速度大小g取10 m/s2.求:
图6
(1)t=0时刻木板的速度大小;
(2)木板的长度.
答案 (1)5 m/s (2) m
解析 (1)对木板和物块:μ1(M+m)g=(M+m)a1
设初始时刻木板速度为v0
由运动学公式:v1=v0-a1t0
代入数据解得:v0=5 m/s
(2)碰撞后,对物块:μ2mg=ma2
对物块,当速度为0时,经历时间t,发生位移x1,则有v1=a2t,x1=t
对木板,由牛顿第二定律:μ2mg+μ1(M+m)g=Ma3
对木板,经历时间t,发生位移x2
x2=v1t-a3t2
木板长度l=x1+x2
联立并代入数据解得l= m.
变式3 (2019·江苏卷·15)如图7所示,质量相等的物块A和B叠放在水平地面上,左边缘对齐.A与B、B与地面间的动摩擦因数均为μ.先敲击A,A立即获得水平向右的初速度,在B上滑动距离L后停下.接着敲击B,B立即获得水平向右的初速度,A、B都向右运动,左边缘再次对齐时恰好相对静止,此后两者一起运动至停下.最大静摩擦力等于滑动摩擦力,重力加速度为g.求:
图7
(1)A被敲击后获得的初速度大小vA;
(2)在左边缘再次对齐的前、后,B运动加速度的大小aB、aB′;
(3)B被敲击后获得的初速度大小vB.
答案 (1) (2)3μg μg (3)2
解析 (1)由牛顿第二定律知,A加速度的大小aA=μg
由匀变速直线运动规律得2aAL=v
解得vA=;
(2)设A、B的质量均为m
对齐前,B所受合外力大小F=3μmg
由牛顿第二定律F=maB,得aB=3μg
对齐后,A、B所受合外力大小F′=2μmg
由牛顿第二定律F′=2maB′,得aB′=μg;
(3)设经过时间t,A、B达到共同速度v,位移分别为xA、xB,A加速度的大小为aA
则v=aAt,v=vB-aBt
xA=aAt2,xB=vBt-aBt2
且xB-xA=L
解得vB=2 .
x2=(24+2-8) m=18 m.
