人教版数学七年级下册10.2 利用频数分布直方图描述数据课件(共29张PPT)
文档属性
| 名称 | 人教版数学七年级下册10.2 利用频数分布直方图描述数据课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-20 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
10.2直方图(1)
情景导入
上节课我们学会了调查全班同学对不同学科的喜爱情况的方法,学习了运用条形图、扇形图、折线图等描述数据的方法,现在如果要调查全校学生的情况,该如何进行呢?这节课我们就来学习另一种描述数据的统计图——直方图。
学习目标
1. 体会数据在现实生活中的作用,理解直方图的特点.
2. 通过观察、思考等数学活动,提高合理思维、推理能力;通过比较、概括,提高归纳总结能力.
3. 培养接触社会环境中数的信息能力,增强对数学学习的兴趣.
复习回顾
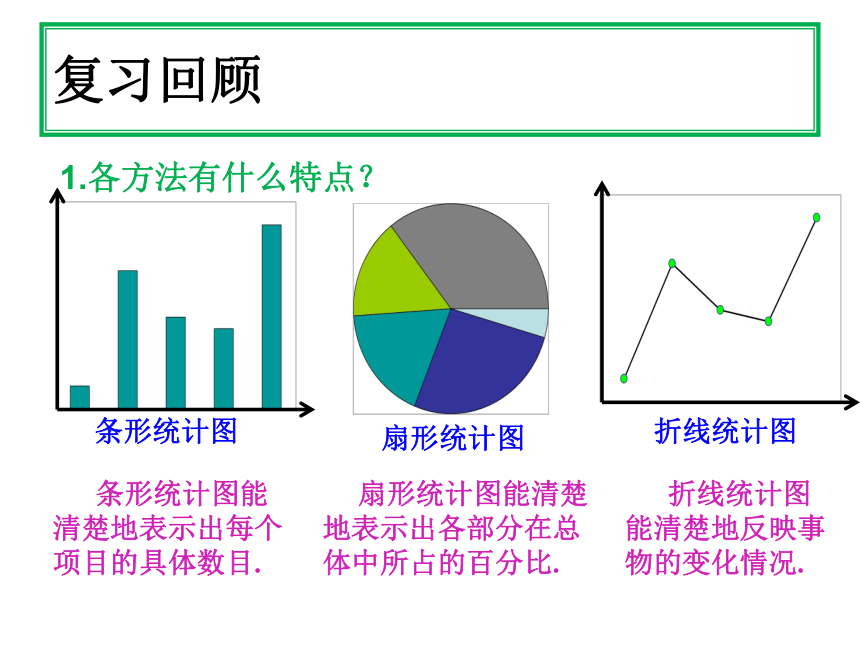
1.各方法有什么特点?
复习回顾
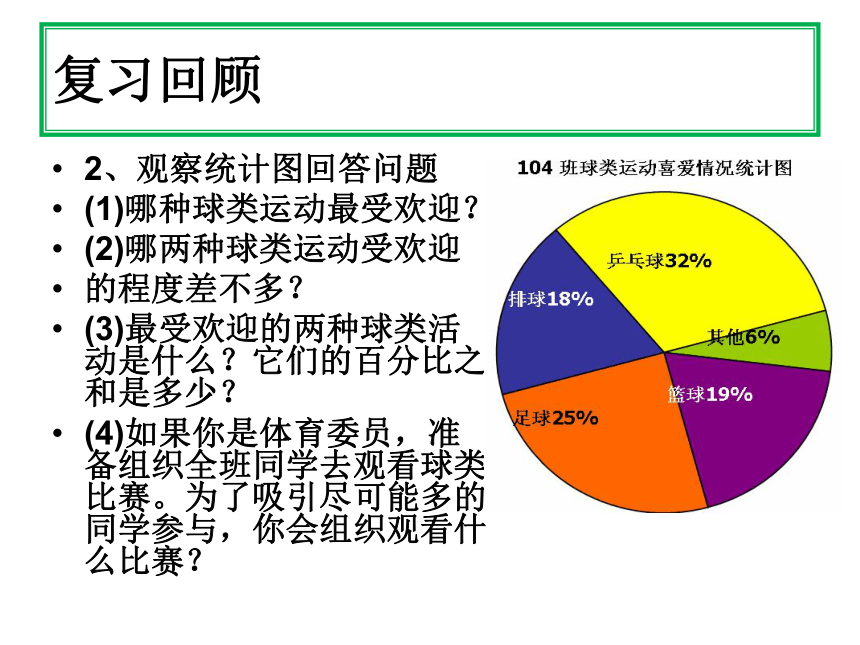
2、观察统计图回答问题
(1)哪种球类运动最受欢迎?
(2)哪两种球类运动受欢迎
的程度差不多?
(3)最受欢迎的两种球类活动是什么?它们的百分比之和是多少?
(4)如果你是体育委员,准备组织全班同学去观看球类比赛。为了吸引尽可能多的同学参与,你会组织观看什么比赛?
复习回顾
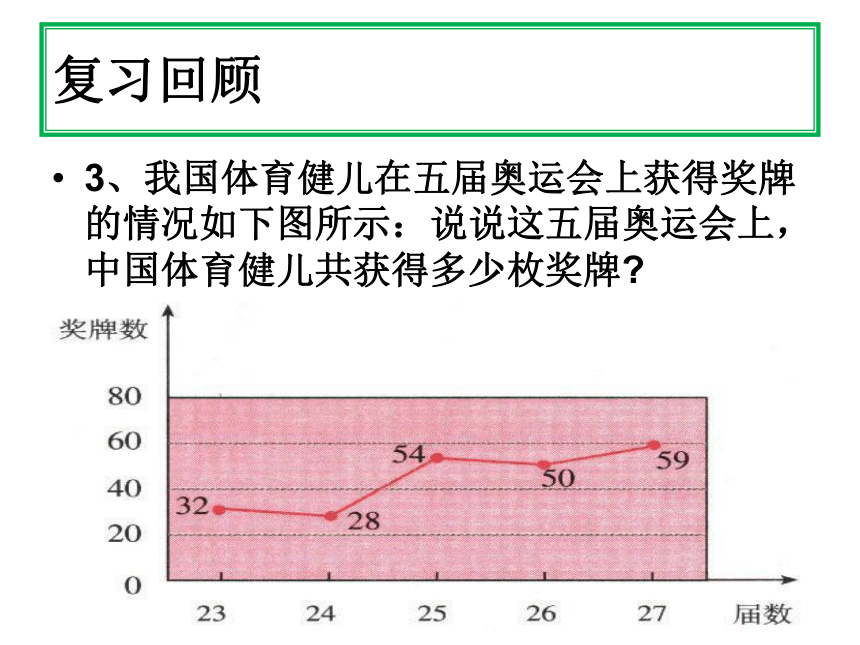
3、我国体育健儿在五届奥运会上获得奖牌的情况如下图所示:说说这五届奥运会上,中国体育健儿共获得多少枚奖牌?
导入新课
为了参加全校各个年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
问题引入
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
选择身高在哪个范围内的学生参加呢?
为了使选取的参赛选手身高比较整齐,需要知道数据的分布情况,即在哪些身高范围的学生比较多,哪些身高范围内的学生人数比较少.为此可以通过对这些数据适当分组来进行整理.
探究新知
1.计算最大值和最小值的差 (极差)
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23 cm.
探究新知
2.决定组距和组数
把所有数据分成若干组,每个小组的两
个端点之间的距离称为组距.
(最大值-最小值)÷组距
所以要将数据分成8组:149≤x<152,152≤x<155,… 170≤x<173.这里组数和组距分别是8和3.
探究新知
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表.
探究新知
2
6
12
19
10
8
4
2
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155~164 cm(不含164 cm)的学生中选队员.
探究新知
身高(x) 划记 频数(学生人数)
149≤x<152
152≤x<155
155≤x<158
158≤x<161
161≤x<164
164≤x<167
167≤x<170
170≤x<173
4、画频数分布直方图
横轴表示各组身高,纵轴表示频数与组距的比值,画出一个个小长方形。
当等距分组时,每个长方形的高表示对应组的频数。
探究新知
身高/cm
频数分布直方图
探究新知
问题1解答
频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小.小长方形的高是频数与组距的比值.
等距分组时,各个小长方形的面积(频数)与高的比是常数(组距),因此画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
探究新知
频数
(学生人数)
身高/㎝
20
15
10
5
0
149 152 155 158 161 164 167 170 173
图10.2-3
等距分组的频数分布直方图
每个长方形的高表示对应组的频数。
2
6
12
19
10
8
4
2
等距分组时,各个小长方形的面积(频数)与高的比值是常数(组距),因此画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
o
身高/cm
频数(学生人数)
5
10
15
20
我们也可以用频数折线图来描述频数分布的情况。频数折线图可以在频数分布直方图的基础上画出来。
直方图的特点:
1、直方图能够显示各组频数分布情况
2、易于显示各组之间频数之间的差别
3、直方图的各长方形通常是连续排列,中间没有空隙。
(1) 计算最大值与最小值的差(极差).
(2) 决定组距与组数.
(4)列频数分布表. 数出每一组频数
(5)绘制频数分布直方图.
横轴表示各组数据,纵轴表示频数, 该组内的频数为高,画出一个个长方形。
(3) 决定分点.
画频数分布直方图的一般步骤:
探究新知
1.通过对直方图的学习,你能说说条形图与直方图有什么相同与不同吗?
探究新知
1:条形图各矩形间有空隙,直方图各矩形间无空隙。
条形图与直方图的区别:
2.直方图可以显示各组频数分布情况,而条形图不能反映这一点。
探究新知
1.大宝同学统计了他家10月份的长途电话清单,并按通话时间画出直方图:
课堂练习
(1)他家这个月一共打了多少次电话?
(2)通话时间不足10分钟的有多少次?
(3)哪个时间范围的通话最多?哪个时间范围的通话少?
25
18
8
10
16
77
43
1到5分钟内
10到15分钟内
课堂练习
2、在对七年级某班的一次数学测验成绩进行统计分析中,各分数段的人数如图所示(分数取正整数, 满分100分),请观察图形,并回答下列问题。
(1)该班有 名学生;
(2)70.5~80.5这一组的频数是 ,频率是 ;
44
14
0.32
课堂练习
3.根据直方图回答问题:
(1)脉搏在 范围的学生最多,有 个人。 (2)脉搏在135---140有 人,160---165有 人,
(3) 全班有 人。
155~160
14
2
11
49
巩固练习
4. 某中学九年级部分同学参加全国初中数学竞赛,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数分布直方图,如图所示,请根据直方图回答下列问题:
(每组含最低分,不含最高分)
巩固练习
(每组含最低分,不含最高分)
4. 某中学九年级部分同学参加全国初中数学竞赛,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数分布直方图,如图所示,请根据直方图回答下列问题:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?(3)图中还提供了其他信息,例如该中学没有获得满分的同学等等。请再写出两条信息。
解:(1)4+6+8+7+5+2=32,所以参加本次数学竞赛
的有32名同学;
(2)(7+5+2)÷32=43.75%,所以该中学的参赛
同学获奖率是43.75 %;
(3)该中学参赛同学的成绩均不低于60分;成绩在
80~90分数段的人数最多。
通过本节学习,我们了解了频数分布的意义及获得一组数据的频数分布的一般步骤:
(1)计算极差;
(2) 决定组距和组数;
(3) 决定分点;
(4) 列出频数分布表;
(5)画出频数分布直方图。
课堂小结
教科书习题10.2第1、2题.
作业
10.2直方图(1)
情景导入
上节课我们学会了调查全班同学对不同学科的喜爱情况的方法,学习了运用条形图、扇形图、折线图等描述数据的方法,现在如果要调查全校学生的情况,该如何进行呢?这节课我们就来学习另一种描述数据的统计图——直方图。
学习目标
1. 体会数据在现实生活中的作用,理解直方图的特点.
2. 通过观察、思考等数学活动,提高合理思维、推理能力;通过比较、概括,提高归纳总结能力.
3. 培养接触社会环境中数的信息能力,增强对数学学习的兴趣.
复习回顾
1.各方法有什么特点?
复习回顾
2、观察统计图回答问题
(1)哪种球类运动最受欢迎?
(2)哪两种球类运动受欢迎
的程度差不多?
(3)最受欢迎的两种球类活动是什么?它们的百分比之和是多少?
(4)如果你是体育委员,准备组织全班同学去观看球类比赛。为了吸引尽可能多的同学参与,你会组织观看什么比赛?
复习回顾
3、我国体育健儿在五届奥运会上获得奖牌的情况如下图所示:说说这五届奥运会上,中国体育健儿共获得多少枚奖牌?
导入新课
为了参加全校各个年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下:
问题引入
158 158 160 168 159 159 151 158 159
168 158 154 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
选择身高在哪个范围内的学生参加呢?
为了使选取的参赛选手身高比较整齐,需要知道数据的分布情况,即在哪些身高范围的学生比较多,哪些身高范围内的学生人数比较少.为此可以通过对这些数据适当分组来进行整理.
探究新知
1.计算最大值和最小值的差 (极差)
在上面的数据中,最小值是149,最大值是172,它们的差是23,说明身高的变化范围是23 cm.
探究新知
2.决定组距和组数
把所有数据分成若干组,每个小组的两
个端点之间的距离称为组距.
(最大值-最小值)÷组距
所以要将数据分成8组:149≤x<152,152≤x<155,… 170≤x<173.这里组数和组距分别是8和3.
探究新知
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表.
探究新知
2
6
12
19
10
8
4
2
从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155~164 cm(不含164 cm)的学生中选队员.
探究新知
身高(x) 划记 频数(学生人数)
149≤x<152
152≤x<155
155≤x<158
158≤x<161
161≤x<164
164≤x<167
167≤x<170
170≤x<173
4、画频数分布直方图
横轴表示各组身高,纵轴表示频数与组距的比值,画出一个个小长方形。
当等距分组时,每个长方形的高表示对应组的频数。
探究新知
身高/cm
频数分布直方图
探究新知
问题1解答
频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小.小长方形的高是频数与组距的比值.
等距分组时,各个小长方形的面积(频数)与高的比是常数(组距),因此画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
探究新知
频数
(学生人数)
身高/㎝
20
15
10
5
0
149 152 155 158 161 164 167 170 173
图10.2-3
等距分组的频数分布直方图
每个长方形的高表示对应组的频数。
2
6
12
19
10
8
4
2
等距分组时,各个小长方形的面积(频数)与高的比值是常数(组距),因此画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
o
身高/cm
频数(学生人数)
5
10
15
20
我们也可以用频数折线图来描述频数分布的情况。频数折线图可以在频数分布直方图的基础上画出来。
直方图的特点:
1、直方图能够显示各组频数分布情况
2、易于显示各组之间频数之间的差别
3、直方图的各长方形通常是连续排列,中间没有空隙。
(1) 计算最大值与最小值的差(极差).
(2) 决定组距与组数.
(4)列频数分布表. 数出每一组频数
(5)绘制频数分布直方图.
横轴表示各组数据,纵轴表示频数, 该组内的频数为高,画出一个个长方形。
(3) 决定分点.
画频数分布直方图的一般步骤:
探究新知
1.通过对直方图的学习,你能说说条形图与直方图有什么相同与不同吗?
探究新知
1:条形图各矩形间有空隙,直方图各矩形间无空隙。
条形图与直方图的区别:
2.直方图可以显示各组频数分布情况,而条形图不能反映这一点。
探究新知
1.大宝同学统计了他家10月份的长途电话清单,并按通话时间画出直方图:
课堂练习
(1)他家这个月一共打了多少次电话?
(2)通话时间不足10分钟的有多少次?
(3)哪个时间范围的通话最多?哪个时间范围的通话少?
25
18
8
10
16
77
43
1到5分钟内
10到15分钟内
课堂练习
2、在对七年级某班的一次数学测验成绩进行统计分析中,各分数段的人数如图所示(分数取正整数, 满分100分),请观察图形,并回答下列问题。
(1)该班有 名学生;
(2)70.5~80.5这一组的频数是 ,频率是 ;
44
14
0.32
课堂练习
3.根据直方图回答问题:
(1)脉搏在 范围的学生最多,有 个人。 (2)脉搏在135---140有 人,160---165有 人,
(3) 全班有 人。
155~160
14
2
11
49
巩固练习
4. 某中学九年级部分同学参加全国初中数学竞赛,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数分布直方图,如图所示,请根据直方图回答下列问题:
(每组含最低分,不含最高分)
巩固练习
(每组含最低分,不含最高分)
4. 某中学九年级部分同学参加全国初中数学竞赛,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数分布直方图,如图所示,请根据直方图回答下列问题:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?(3)图中还提供了其他信息,例如该中学没有获得满分的同学等等。请再写出两条信息。
解:(1)4+6+8+7+5+2=32,所以参加本次数学竞赛
的有32名同学;
(2)(7+5+2)÷32=43.75%,所以该中学的参赛
同学获奖率是43.75 %;
(3)该中学参赛同学的成绩均不低于60分;成绩在
80~90分数段的人数最多。
通过本节学习,我们了解了频数分布的意义及获得一组数据的频数分布的一般步骤:
(1)计算极差;
(2) 决定组距和组数;
(3) 决定分点;
(4) 列出频数分布表;
(5)画出频数分布直方图。
课堂小结
教科书习题10.2第1、2题.
作业
