1.1《探究动量变化与冲量的关系》第1课时—沪教版(上海科教版)高中物理选修3-5课件 (共16张PPT)
文档属性
| 名称 | 1.1《探究动量变化与冲量的关系》第1课时—沪教版(上海科教版)高中物理选修3-5课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 159.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-21 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
动量与冲量
《探究动量变化与冲量的关系》第1课时
问题一?
你敢踢对面飞来的足球吗?
你敢踢对面飞来的铅球吗?
一、动量 P
1)定义:运动物体的质量m和速度v的乘积叫做物体的动量。
2)特点说明:
(1)矢量性:方向与该时刻速度的方向相同
单位:千克·米/秒,( kg·m/s)
(2)瞬时性:动量P是状态量,与某时刻物体的m和v对应
(3)相对性:v与参考系选择有关,常以地面为参考系。
运算法则:运算遵循平行四边形定则或者三角形法则。
(4)动量的变化:是物体末动量与初动量的矢量差
一维空间时:选定正方向,转化为代数运算。
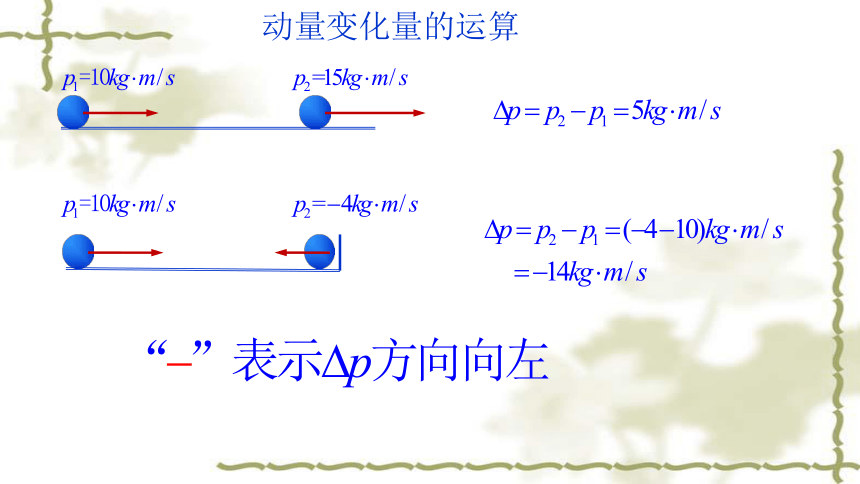
动量变化量的运算
(5)P的大小与EK的关系:
P=mv
例1、在水平面上有甲、乙两滑块,其质量分别为m1=1.0kg和m2=2.0kg,且沿同一直线运动,若以甲运动的方向为正方向,由甲的速度υ1=10.0m/s,乙的速度υ2=-5.0m/s,甲的动量大小是 ,
方向 ;乙的动量大小是 ,方向 .
10.0kg·m/s
10.0kg·m/s
与甲运动方向相同
与甲运动方向相反
例2、一个质量为0.5kg的足球,以20m/s的速度向东运动,受到足球队员的作用力后,改为以20m/s的速度向西运动,足球在受足球队员作用前瞬间的动量p是多少?作用后瞬间的动量p?又是多少?足球的动量改变量Δp是多少?
以向东为正方向,
求一维空间物体的动量先要规定正方向,确定物体的动量的变化Δp,一定要注意到动量的方向性。
例3、一物体放在光滑的水平面上,有一颗子弹以水平速度υ0射向它,可能有三种情况:⑴子弹反弹回去;⑵子弹射中物体后留在物体中,二者以相同的速度一起运动;⑶子弹射穿物体后各以大小不同但方向相同的速度运动。在这三种情况中,子弹动量的改变量最大的是 种情况。
⑴
例4、质量为m的质点以速度υ绕半径R的圆周轨道做匀速圆周运动,在半个周期内动量的改变量大小为 ( )
A.0 B.mυ C.2mυ D.无法确定
C
例4、一个质量为2kg的物体以某一速度在空中水平抛出,飞行的时间为5s,求物体从抛出到落地过程中动量的变化量。不计空气阻力(重力加速度g=10m/s2)
物体做平抛运动,水平方向速度的变化量为零,即水平方向动量的变化也为零;在竖直方向,速度的变化量即为末速度,?υ=υ=gt=50m/s,物体动量变化量只有竖直方向的动量变化Δp= m?υ =100 kgm/s,方向竖直向下。
力对物体作用的时间不一样,产生的作用效果相同吗?
看来很多情况下,力对时间的积累产生的效果不同,有必要引入一个反映力对时间积累相关的物理量
1)概念:力F与力的作用时间t的乘积叫做冲量
二、力的冲量 I
2)特点说明:
(1)是矢量:方向恒定的力冲量方向与力同向定(变力的冲量方向与力的方向变化及过程有关)
定义式: 单位:N s
(2)过程量,描述力的时间积累效应。
(3) 绝对性:与参考系无关
二、力的冲量 I
1.恒力的冲量
计算公式:I=Ft
2.F-t图像
t/s
F/N
t1
t2
I=Ft 图像与时间轴围成的面积
二、力的冲量 I
1.变力的冲量
由于F变化,所以不能使用I=Ft计算
2.F-t图像
t/s
F/N
t1
t2
可以回顾我们怎么样计算匀变速直线运动的位移
(1)将这段时间划分为许多小段时间段 ,由于每个小时间段时间很短,所以认为这小段时间内力F为恒力,所以F 为这小短时间内的冲量。
(2)将每小段时间内的冲量加起来,就是F-t图像与时间轴围成的面积。
例题1、一个质量为5Kg的物体从离地面20m的高处自由下落。不计空气阻力,试求在下落的这段时间内物体所受重力的冲量。
冲量必须是物体某个力某段时间内所受力的冲量
两个物理量使用说明
1、动量时状态量,所以一定指明什么物体?什么时刻?
2、冲量是过程量,说明时一定明确是哪个过程?哪个力的冲量?
3、动量、动量的变化量、冲量都是矢量,必须考虑着些量的方向性。
4、由于动量、动量的变化量、冲量都是矢量,所以运算时必须遵循矢量的运算法则
5、为方便矢量的运算,首先规定参考方向,一维度运算时,有了参考方向,将矢量的运算转换成代数运算
动量与冲量
《探究动量变化与冲量的关系》第1课时
问题一?
你敢踢对面飞来的足球吗?
你敢踢对面飞来的铅球吗?
一、动量 P
1)定义:运动物体的质量m和速度v的乘积叫做物体的动量。
2)特点说明:
(1)矢量性:方向与该时刻速度的方向相同
单位:千克·米/秒,( kg·m/s)
(2)瞬时性:动量P是状态量,与某时刻物体的m和v对应
(3)相对性:v与参考系选择有关,常以地面为参考系。
运算法则:运算遵循平行四边形定则或者三角形法则。
(4)动量的变化:是物体末动量与初动量的矢量差
一维空间时:选定正方向,转化为代数运算。
动量变化量的运算
(5)P的大小与EK的关系:
P=mv
例1、在水平面上有甲、乙两滑块,其质量分别为m1=1.0kg和m2=2.0kg,且沿同一直线运动,若以甲运动的方向为正方向,由甲的速度υ1=10.0m/s,乙的速度υ2=-5.0m/s,甲的动量大小是 ,
方向 ;乙的动量大小是 ,方向 .
10.0kg·m/s
10.0kg·m/s
与甲运动方向相同
与甲运动方向相反
例2、一个质量为0.5kg的足球,以20m/s的速度向东运动,受到足球队员的作用力后,改为以20m/s的速度向西运动,足球在受足球队员作用前瞬间的动量p是多少?作用后瞬间的动量p?又是多少?足球的动量改变量Δp是多少?
以向东为正方向,
求一维空间物体的动量先要规定正方向,确定物体的动量的变化Δp,一定要注意到动量的方向性。
例3、一物体放在光滑的水平面上,有一颗子弹以水平速度υ0射向它,可能有三种情况:⑴子弹反弹回去;⑵子弹射中物体后留在物体中,二者以相同的速度一起运动;⑶子弹射穿物体后各以大小不同但方向相同的速度运动。在这三种情况中,子弹动量的改变量最大的是 种情况。
⑴
例4、质量为m的质点以速度υ绕半径R的圆周轨道做匀速圆周运动,在半个周期内动量的改变量大小为 ( )
A.0 B.mυ C.2mυ D.无法确定
C
例4、一个质量为2kg的物体以某一速度在空中水平抛出,飞行的时间为5s,求物体从抛出到落地过程中动量的变化量。不计空气阻力(重力加速度g=10m/s2)
物体做平抛运动,水平方向速度的变化量为零,即水平方向动量的变化也为零;在竖直方向,速度的变化量即为末速度,?υ=υ=gt=50m/s,物体动量变化量只有竖直方向的动量变化Δp= m?υ =100 kgm/s,方向竖直向下。
力对物体作用的时间不一样,产生的作用效果相同吗?
看来很多情况下,力对时间的积累产生的效果不同,有必要引入一个反映力对时间积累相关的物理量
1)概念:力F与力的作用时间t的乘积叫做冲量
二、力的冲量 I
2)特点说明:
(1)是矢量:方向恒定的力冲量方向与力同向定(变力的冲量方向与力的方向变化及过程有关)
定义式: 单位:N s
(2)过程量,描述力的时间积累效应。
(3) 绝对性:与参考系无关
二、力的冲量 I
1.恒力的冲量
计算公式:I=Ft
2.F-t图像
t/s
F/N
t1
t2
I=Ft 图像与时间轴围成的面积
二、力的冲量 I
1.变力的冲量
由于F变化,所以不能使用I=Ft计算
2.F-t图像
t/s
F/N
t1
t2
可以回顾我们怎么样计算匀变速直线运动的位移
(1)将这段时间划分为许多小段时间段 ,由于每个小时间段时间很短,所以认为这小段时间内力F为恒力,所以F 为这小短时间内的冲量。
(2)将每小段时间内的冲量加起来,就是F-t图像与时间轴围成的面积。
例题1、一个质量为5Kg的物体从离地面20m的高处自由下落。不计空气阻力,试求在下落的这段时间内物体所受重力的冲量。
冲量必须是物体某个力某段时间内所受力的冲量
两个物理量使用说明
1、动量时状态量,所以一定指明什么物体?什么时刻?
2、冲量是过程量,说明时一定明确是哪个过程?哪个力的冲量?
3、动量、动量的变化量、冲量都是矢量,必须考虑着些量的方向性。
4、由于动量、动量的变化量、冲量都是矢量,所以运算时必须遵循矢量的运算法则
5、为方便矢量的运算,首先规定参考方向,一维度运算时,有了参考方向,将矢量的运算转换成代数运算
同课章节目录
