高中数学人教B版必修三:复习——围绕三角函数概念构建知识体系 课件(67张ppt)
文档属性
| 名称 | 高中数学人教B版必修三:复习——围绕三角函数概念构建知识体系 课件(67张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 17.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 00:00:00 | ||
图片预览







文档简介
(共67张PPT)
复习——围绕三角函数概念构建知识体系
高一年级 数学
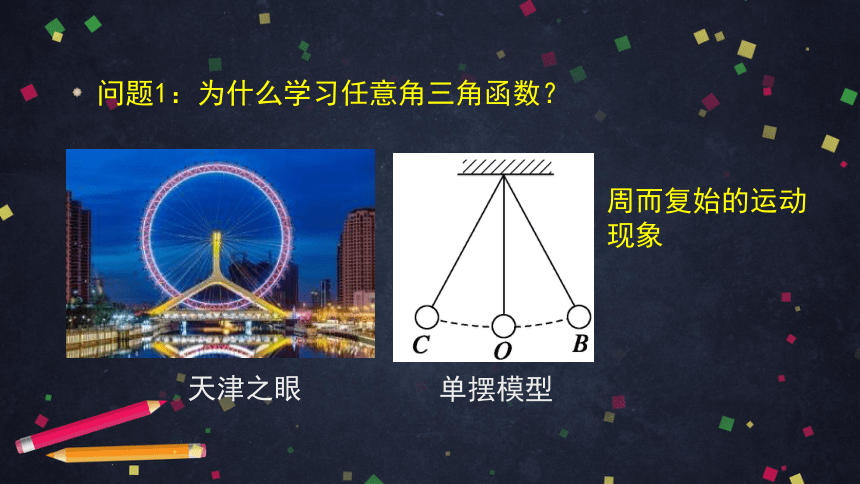
周而复始的运动现象
问题1:为什么学习任意角三角函数?
天津之眼
单摆模型
旋转运动—角度
二者之间的关系?
问题1:为什么学习任意角三角函数?
平移运动—距离
三角函数是最典型的周期函数
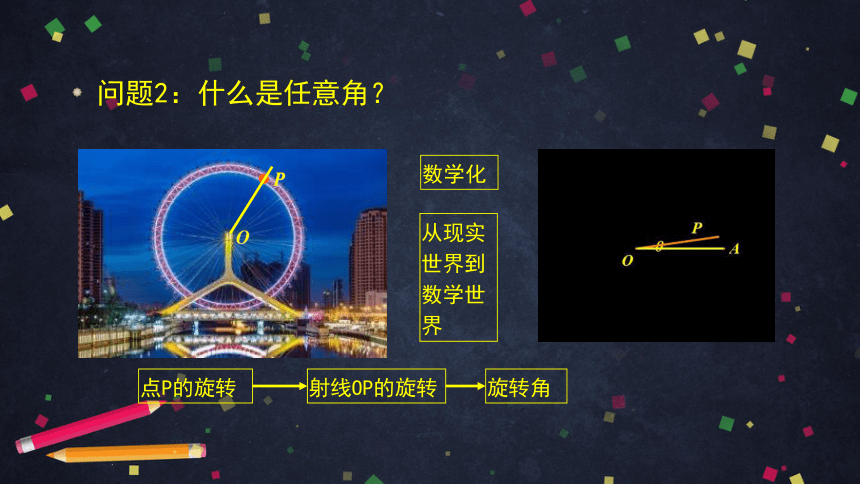
问题2:什么是任意角?
P
O
数学化
点P的旋转
射线OP的旋转
旋转角
从现实世界到数学世界
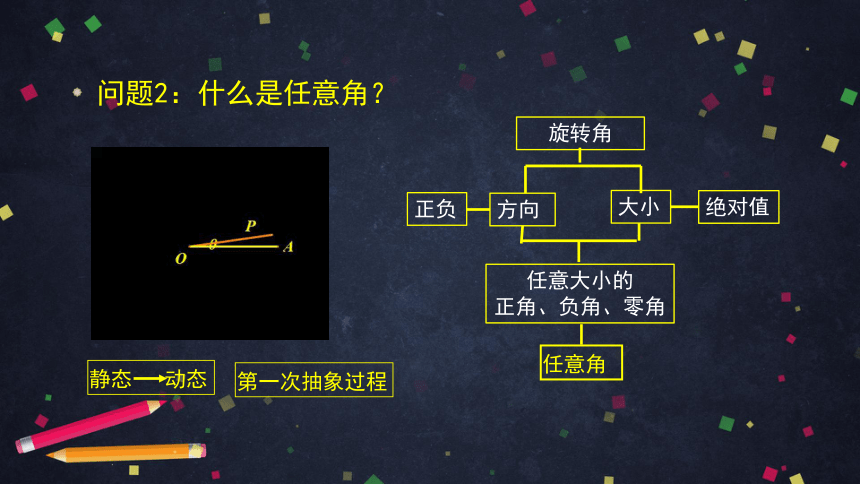
问题2:什么是任意角?
静态 动态
第一次抽象过程
旋转角
任意大小的
正角、负角、零角
方向
大小
正负
绝对值
任意角
P
O
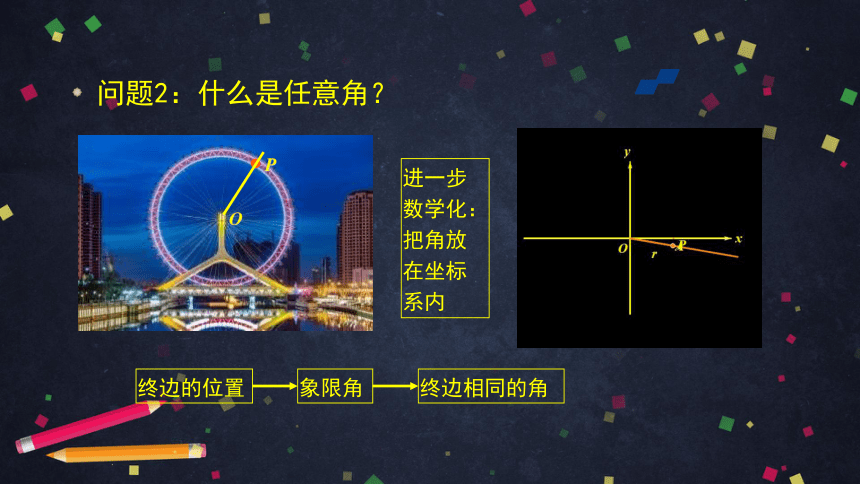
进一步数学化:把角放在坐标系内
问题2:什么是任意角?
终边的位置
象限角
终边相同的角
问题1
的旋转——角度 变化
问题3:为什么要引入弧度制?
的旋转——点 离地面的高度 米
?
用圆弧的长来度量角。
:高度,单位:米,十进制
:角度,单位:度,六十进制
问题3:为什么要引入弧度制?
?
弧度制
实数
角
实现“角度”与“距离”在度量上的统一
问题3:为什么要引入弧度制?
角的运算与实数运算的统一
问题2
C
如图所示,在圆 中,
,求弓形 的周长。
O
x
y
分析:在 内,
终边在 x 轴上的角有两个: 和
,与这两个角终边相同的角
的组成的集合依次为
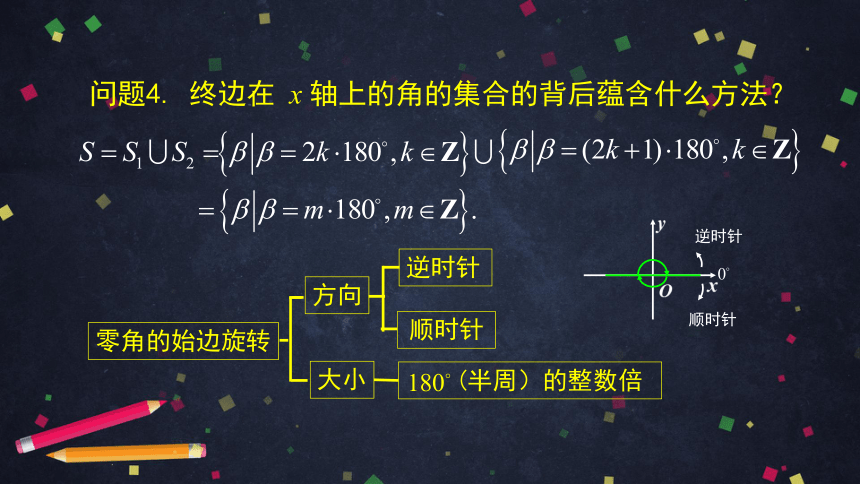
问题4. 终边在 x 轴上的角的集合的背后蕴含什么方法?
问题4. 终边在 x 轴上的角的集合的背后蕴含什么方法?
零角的始边旋转
大小
方向
顺时针
(半周)的整数倍
逆时针
O
x
y
逆时针
顺时针
变式1. 终边在 y 轴上的角的集合是_______________
角 的终边按照逆时针或者顺时针旋转,
每次旋转 (半周)的整数倍.
变式2. 终边在坐标轴上的角的集合是_______________
零角的终边按照逆时针或者顺时针旋转,
每次旋转 (四分之一周)的整数倍.
变式3. 的终边与 终边的关系是______.
角 的终边按照逆时针或者顺时针旋转,每次旋转 (六分之一周)的整数倍得到角 的终边.
揭示角的加减运算的几何意义:对应角的终边按照逆时针、顺时针进行旋转。
问题5:任意角的三角函数是如何定义的?
A
点
P
O
点 离地面的高度?
问题5:任意角的三角函数是如何定义的?
在 终边上任取一点 ,
O
x
y
P(x,y)
M
第二次抽象:建立任意角为自变量的函数
比值只与终边的位置有关,与 无关
问题5:任意角的三角函数是如何定义的?
y
o
x
M
终边与单位圆的交点的
第三次抽象:三角函数的单位圆直观模型.
令
终边重合
转化为同一个角
终边具有对称关系
诱导公式
没有对称关系
两角和与差的三角函数
终边固定
、 、 间静态的方程关系
终边变化
、 随 变化的函数关系
问题6:运用三角函数概念研究问题的路径是怎样的?
任意角的三角函数概念
与旋转角
的关系
任意角
动态
旋转角
的位置
旋转
同角三角函数的基本(固定)关系
、 、 的固定关系
平方关系
商数关系
角 终边固定
y
o
x
M
同角三角函数的基本(固定)关系
你还能推出哪些基本关系?可以参看教材第25页:拓展阅读
O
x
y
P(x,y)
M
问题7.同角三角函数基本关系的实质?知一求其它原因?
实质.揭示同一个角的六种三角函数之间固有的关系,是一种静态的方程关系。
问题7.同角三角函数基本关系的实质?知一求其它原因?
二次方程(组),2个方程,3个未知数
从运算角度分析:
已知
已知
,解方程组
从形的角度分析:
问题7.同角三角函数基本关系的实质?知一求其它原因?
y
o
x
M
在 中,已知任一直角边,或已知两 条直角边的比值,可确定三角形.
同角三角函数的基本关系的应用
求值
化简与证明
解方程组
整体代换
分析恒等式中的:角、名称、次数、结构
公式:正用、逆用、变形用
问题8.应用同角三角函数基本关系求值情境有哪些?
已知角 所在象限
角 所在象限不确定
已知角 的一种三角函数值
与 之间的关系
y
o
x
M
分析:(1)方程思想
解方程组求解
问题9. 已知 ,求 的值.
y
o
x
(2) 所在的象限
解:由题意和同角三角函数的基本关系式,有
,解得
消去 得
或
y
o
x
问题9. 已知 ,求 的值.
若
则
所以
得
由已知
则
y
o
x
M
缩小角的范围
分析:
2.三个代数式间的联系——整体代换
1.方程思想(已经解决)
结论:三个代数式,知一求二
变式.已知 ,求 ,
的值.
解:因为
所以
所以
因为
所以
变式.已知 ,求 ,
的值.
问题10.终边有对称关系的两个角的函数值间的关系如何求得?
诱导公式是特殊位置的两个角的三角函数值关系的解释!
角 的终边 与角 的终边 关于 轴对称
诱导公式的得出路径:
诱导公式
两个角的终边的对称关系
两个角的终边与单位圆的交点坐标间的关系
两个三角函数值间的关系
诱导公式揭示:三角函数的性质与圆的对称性
周期性,
奇偶性,正弦函数是奇函数
诱导公式揭示:三角函数的性质与圆的对称性
圆的旋转的对称性
诱导公式为什么能揭示三角函数的性质?
三角函数的性质
角 的终边
的对称关系
与
与
数学家项武义在其著的《基础几何学》第三章
“圆与三角学”中谈到:
正弦函数、余弦函数是一对源于圆周运动,密切配合的周期函数,它们是解析几何学和周期函数的分析学中最为基础和重要的函数;而正弦、余弦函数的基本性质乃是圆的几何性质(主要是其对称性)的直观反映(解析表述)
三角函数又称作圆函数
诱导公式其它作用:简化运算
负化正、大化小、化成锐角好求值
问题11. 三角函数的自变量是谁?
角 变化
、 随
变化情况
正弦
余弦
正切
三角函数
y
o
x
y
o
x
问题12. 如何通过三角函数概念得到三角函数性质?
函数性质:函数值 随自变量 变化而变化过程中呈现出的规律性和不变性。
问题12. 如何通过三角函数概念得到三角函数性质?
性质一般包括:定义域、对称性、特殊点(零点)、函数值正负区间、周期性、单调性、最值、值域。
研究载体:概念、解析式、图像、代数运算、直观模型
以正弦函数
为例
1.定义域
正角
零角
负角
转角
定义域为
问题12. 如何通过三角函数概念得到三角函数性质?
2.奇偶性
代数特征:
自变量互为相反数时,函数值也互为相反数
数
形
正弦函数
正弦函数是奇函数,图像关于原点中心对称
的中点始终是
图像上
数
形
3.对称性
正弦函数
代数特征:
两个自变量和为 时,对应函数值互为相反数
图像上
的中点始终是
正弦函数的图像是中心对称图形,
对称中点是
数
形
3.对称性
正弦函数
代数特征:两个自变量和为 时,对应函数值相等。
3.对称性
正弦函数图像关于直线 轴对称
图像上
,两个点的横坐标
关于 为中点坐标时,对应点的纵坐标相等
3.对称性
正弦函数
代数特征:两个自变量和为 时函数值相等
数
形
图像上
横坐标关于 为中点坐标时,对应点的纵坐标相等
正弦函数的图像是轴对称图形,
对称轴:
正弦函数 图像
周期:
最小正周期:
正弦函数
4.周期性
数
形
正弦函数
5.单调性
数
形
在区间
递增
在区间
递减
y
o
x
正弦函数
5.单调性
6.值域(最值)
当
时,
当
时,
值域:
正弦函数
正弦函数的零点是
正弦函数
7.零点
形
数
,角的终边落在 轴上
令
我们还可以根据三角函数概念和性质得到三角函数图像,通过观察图像的几何特征得到三角函数性质,但是三角函数概念是研究三角函数性质的根本,单位圆和图像是三角函数性质的两种直观表示.
一点认识:
P
O
问题13:点P距离地面的高度h与旋转时间t的关系?
到地面的高 米 ,从 开始计时,旋转角速度是 弧度/分钟,
旋转半径 米,则经过 分钟后,点 离地面的高度为多少米?
到地面的高 米 ,从 开始计时,旋转角速度是 弧度/分钟,
旋转半径 米,则经过 分钟后,点 离地面的高度为多少米?
P
问题13:点P距离地面的高度h与时间t的关系?
P
经过 分钟, ,
在 中,
所以点 距地面的高度
问题13:点P距离地面的高度h与时间t的关系?
正弦型函数
小结:
P
用数学的眼光看世界
任意角、
任意角的
三角函数概念
现实世界
数学世界
y
o
x
M
用数学的思维分析世界
任意角的三角函数概念
同角三角函数基本关系
诱导公式
三角函数性质和图像
小结:
在数学的世界里
建构正弦型函数
用数学模型解释世界
小结:
数学世界
现实世界
三角函数的概念
与旋转角
的关系
任意角
动态
旋转角
的位置
旋转
周期性运动与变化规律
知识体系:
终边相同
转化为单个角
终边具有对称关系的两个角
诱导公式
任意两个位置
两角和与差的三角函数
角 固定
同角三角函数的基本关系
角 变化
三角函数
运动与变化的观点
关键词
动态函数关系
静态方程关系
作业:
写一篇小论文:
题目:
为什么三角函数的概念是三角函数一章的核心?
感谢收看,下一讲我们看:
研究函数性质的方法再认识
复习——围绕三角函数概念构建知识体系
高一年级 数学
周而复始的运动现象
问题1:为什么学习任意角三角函数?
天津之眼
单摆模型
旋转运动—角度
二者之间的关系?
问题1:为什么学习任意角三角函数?
平移运动—距离
三角函数是最典型的周期函数
问题2:什么是任意角?
P
O
数学化
点P的旋转
射线OP的旋转
旋转角
从现实世界到数学世界
问题2:什么是任意角?
静态 动态
第一次抽象过程
旋转角
任意大小的
正角、负角、零角
方向
大小
正负
绝对值
任意角
P
O
进一步数学化:把角放在坐标系内
问题2:什么是任意角?
终边的位置
象限角
终边相同的角
问题1
的旋转——角度 变化
问题3:为什么要引入弧度制?
的旋转——点 离地面的高度 米
?
用圆弧的长来度量角。
:高度,单位:米,十进制
:角度,单位:度,六十进制
问题3:为什么要引入弧度制?
?
弧度制
实数
角
实现“角度”与“距离”在度量上的统一
问题3:为什么要引入弧度制?
角的运算与实数运算的统一
问题2
C
如图所示,在圆 中,
,求弓形 的周长。
O
x
y
分析:在 内,
终边在 x 轴上的角有两个: 和
,与这两个角终边相同的角
的组成的集合依次为
问题4. 终边在 x 轴上的角的集合的背后蕴含什么方法?
问题4. 终边在 x 轴上的角的集合的背后蕴含什么方法?
零角的始边旋转
大小
方向
顺时针
(半周)的整数倍
逆时针
O
x
y
逆时针
顺时针
变式1. 终边在 y 轴上的角的集合是_______________
角 的终边按照逆时针或者顺时针旋转,
每次旋转 (半周)的整数倍.
变式2. 终边在坐标轴上的角的集合是_______________
零角的终边按照逆时针或者顺时针旋转,
每次旋转 (四分之一周)的整数倍.
变式3. 的终边与 终边的关系是______.
角 的终边按照逆时针或者顺时针旋转,每次旋转 (六分之一周)的整数倍得到角 的终边.
揭示角的加减运算的几何意义:对应角的终边按照逆时针、顺时针进行旋转。
问题5:任意角的三角函数是如何定义的?
A
点
P
O
点 离地面的高度?
问题5:任意角的三角函数是如何定义的?
在 终边上任取一点 ,
O
x
y
P(x,y)
M
第二次抽象:建立任意角为自变量的函数
比值只与终边的位置有关,与 无关
问题5:任意角的三角函数是如何定义的?
y
o
x
M
终边与单位圆的交点的
第三次抽象:三角函数的单位圆直观模型.
令
终边重合
转化为同一个角
终边具有对称关系
诱导公式
没有对称关系
两角和与差的三角函数
终边固定
、 、 间静态的方程关系
终边变化
、 随 变化的函数关系
问题6:运用三角函数概念研究问题的路径是怎样的?
任意角的三角函数概念
与旋转角
的关系
任意角
动态
旋转角
的位置
旋转
同角三角函数的基本(固定)关系
、 、 的固定关系
平方关系
商数关系
角 终边固定
y
o
x
M
同角三角函数的基本(固定)关系
你还能推出哪些基本关系?可以参看教材第25页:拓展阅读
O
x
y
P(x,y)
M
问题7.同角三角函数基本关系的实质?知一求其它原因?
实质.揭示同一个角的六种三角函数之间固有的关系,是一种静态的方程关系。
问题7.同角三角函数基本关系的实质?知一求其它原因?
二次方程(组),2个方程,3个未知数
从运算角度分析:
已知
已知
,解方程组
从形的角度分析:
问题7.同角三角函数基本关系的实质?知一求其它原因?
y
o
x
M
在 中,已知任一直角边,或已知两 条直角边的比值,可确定三角形.
同角三角函数的基本关系的应用
求值
化简与证明
解方程组
整体代换
分析恒等式中的:角、名称、次数、结构
公式:正用、逆用、变形用
问题8.应用同角三角函数基本关系求值情境有哪些?
已知角 所在象限
角 所在象限不确定
已知角 的一种三角函数值
与 之间的关系
y
o
x
M
分析:(1)方程思想
解方程组求解
问题9. 已知 ,求 的值.
y
o
x
(2) 所在的象限
解:由题意和同角三角函数的基本关系式,有
,解得
消去 得
或
y
o
x
问题9. 已知 ,求 的值.
若
则
所以
得
由已知
则
y
o
x
M
缩小角的范围
分析:
2.三个代数式间的联系——整体代换
1.方程思想(已经解决)
结论:三个代数式,知一求二
变式.已知 ,求 ,
的值.
解:因为
所以
所以
因为
所以
变式.已知 ,求 ,
的值.
问题10.终边有对称关系的两个角的函数值间的关系如何求得?
诱导公式是特殊位置的两个角的三角函数值关系的解释!
角 的终边 与角 的终边 关于 轴对称
诱导公式的得出路径:
诱导公式
两个角的终边的对称关系
两个角的终边与单位圆的交点坐标间的关系
两个三角函数值间的关系
诱导公式揭示:三角函数的性质与圆的对称性
周期性,
奇偶性,正弦函数是奇函数
诱导公式揭示:三角函数的性质与圆的对称性
圆的旋转的对称性
诱导公式为什么能揭示三角函数的性质?
三角函数的性质
角 的终边
的对称关系
与
与
数学家项武义在其著的《基础几何学》第三章
“圆与三角学”中谈到:
正弦函数、余弦函数是一对源于圆周运动,密切配合的周期函数,它们是解析几何学和周期函数的分析学中最为基础和重要的函数;而正弦、余弦函数的基本性质乃是圆的几何性质(主要是其对称性)的直观反映(解析表述)
三角函数又称作圆函数
诱导公式其它作用:简化运算
负化正、大化小、化成锐角好求值
问题11. 三角函数的自变量是谁?
角 变化
、 随
变化情况
正弦
余弦
正切
三角函数
y
o
x
y
o
x
问题12. 如何通过三角函数概念得到三角函数性质?
函数性质:函数值 随自变量 变化而变化过程中呈现出的规律性和不变性。
问题12. 如何通过三角函数概念得到三角函数性质?
性质一般包括:定义域、对称性、特殊点(零点)、函数值正负区间、周期性、单调性、最值、值域。
研究载体:概念、解析式、图像、代数运算、直观模型
以正弦函数
为例
1.定义域
正角
零角
负角
转角
定义域为
问题12. 如何通过三角函数概念得到三角函数性质?
2.奇偶性
代数特征:
自变量互为相反数时,函数值也互为相反数
数
形
正弦函数
正弦函数是奇函数,图像关于原点中心对称
的中点始终是
图像上
数
形
3.对称性
正弦函数
代数特征:
两个自变量和为 时,对应函数值互为相反数
图像上
的中点始终是
正弦函数的图像是中心对称图形,
对称中点是
数
形
3.对称性
正弦函数
代数特征:两个自变量和为 时,对应函数值相等。
3.对称性
正弦函数图像关于直线 轴对称
图像上
,两个点的横坐标
关于 为中点坐标时,对应点的纵坐标相等
3.对称性
正弦函数
代数特征:两个自变量和为 时函数值相等
数
形
图像上
横坐标关于 为中点坐标时,对应点的纵坐标相等
正弦函数的图像是轴对称图形,
对称轴:
正弦函数 图像
周期:
最小正周期:
正弦函数
4.周期性
数
形
正弦函数
5.单调性
数
形
在区间
递增
在区间
递减
y
o
x
正弦函数
5.单调性
6.值域(最值)
当
时,
当
时,
值域:
正弦函数
正弦函数的零点是
正弦函数
7.零点
形
数
,角的终边落在 轴上
令
我们还可以根据三角函数概念和性质得到三角函数图像,通过观察图像的几何特征得到三角函数性质,但是三角函数概念是研究三角函数性质的根本,单位圆和图像是三角函数性质的两种直观表示.
一点认识:
P
O
问题13:点P距离地面的高度h与旋转时间t的关系?
到地面的高 米 ,从 开始计时,旋转角速度是 弧度/分钟,
旋转半径 米,则经过 分钟后,点 离地面的高度为多少米?
到地面的高 米 ,从 开始计时,旋转角速度是 弧度/分钟,
旋转半径 米,则经过 分钟后,点 离地面的高度为多少米?
P
问题13:点P距离地面的高度h与时间t的关系?
P
经过 分钟, ,
在 中,
所以点 距地面的高度
问题13:点P距离地面的高度h与时间t的关系?
正弦型函数
小结:
P
用数学的眼光看世界
任意角、
任意角的
三角函数概念
现实世界
数学世界
y
o
x
M
用数学的思维分析世界
任意角的三角函数概念
同角三角函数基本关系
诱导公式
三角函数性质和图像
小结:
在数学的世界里
建构正弦型函数
用数学模型解释世界
小结:
数学世界
现实世界
三角函数的概念
与旋转角
的关系
任意角
动态
旋转角
的位置
旋转
周期性运动与变化规律
知识体系:
终边相同
转化为单个角
终边具有对称关系的两个角
诱导公式
任意两个位置
两角和与差的三角函数
角 固定
同角三角函数的基本关系
角 变化
三角函数
运动与变化的观点
关键词
动态函数关系
静态方程关系
作业:
写一篇小论文:
题目:
为什么三角函数的概念是三角函数一章的核心?
感谢收看,下一讲我们看:
研究函数性质的方法再认识
