高中数学人教B版必修三:已知三角函数值求角 课件(41张ppt)
文档属性
| 名称 | 高中数学人教B版必修三:已知三角函数值求角 课件(41张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-23 00:00:00 | ||
图片预览









文档简介
(共41张PPT)
高一年级 数学
已知三角函数值求角
问题:已知三角函数值或值的范围,如何求角的值或角的范围?
角
三角函数值
?
(1)已知 ,你能求出满足条件的角 吗?
(2)已知 ,你能求出 的取值范围吗?
问题:可以直接运算求解吗?
用哪些知识和方法来解决这类问题?
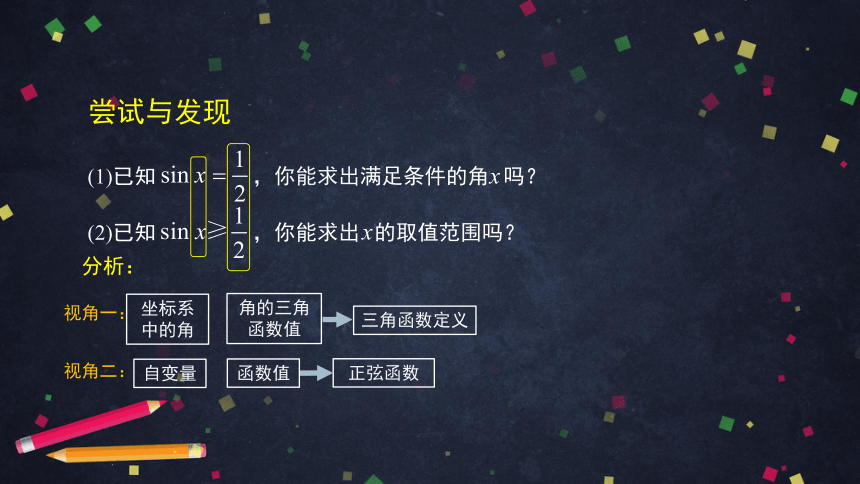
尝试与发现
(1)已知 ,你能求出满足条件的角 吗?
(2)已知 ,你能求出 的取值范围吗?
尝试与发现
三角函数定义
坐标系中的角
角的三角函数值
分析:
正弦函数
自变量
函数值
视角一:
视角二:
y
o
x
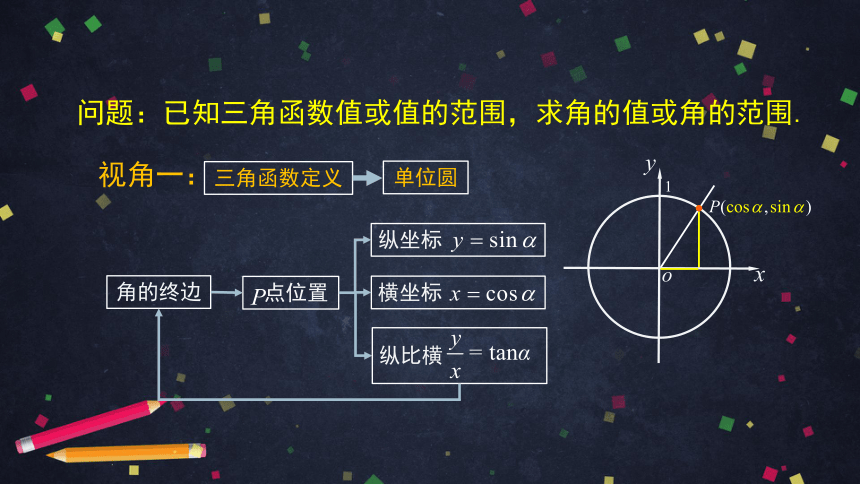
问题:已知三角函数值或值的范围,求角的值或角的范围.
角的终边
点位置
纵坐标
横坐标
纵比横
视角一:
三角函数定义
单位圆
问题:已知三角函数值或值的范围,求角的值或角的范围.
函数
方程
不等式
(不等号也可以是<、≤、>)
视角二:
三角函数的性质与图像
问题:坐标系中哪些信息对应 中的x与y?
角的终边
点P
纵坐标
角 值
正弦值
数
形
视角一:
三角函数定义
单位圆
对 应
对 应
y
o
x
已知三角函数值或值的范围,求角的值或角的范围.
问题:随着角的终边的旋转,正弦值是怎样变化的?
视角一:
三角函数定义
单位圆
在 内,
在 内,
……
x
y
o
已知三角函数值或值的范围,求角的值或角的范围.
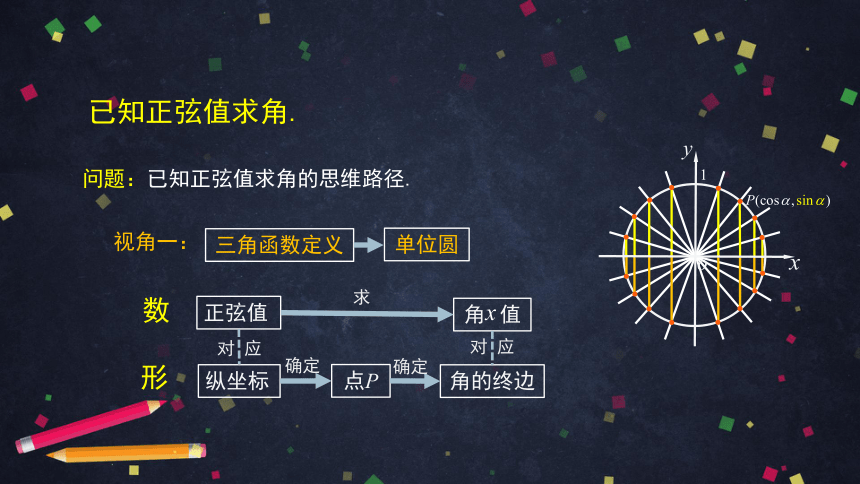
问题:已知正弦值求角的思维路径.
已知正弦值求角.
角的终边
点P
纵坐标
角 值
正弦值
数
形
视角一:
三角函数定义
单位圆
x
y
o
求
对 应
对 应
确定
确定
问题:方程有几个解?怎样表达?
逆时针旋转一圈
顺时针旋转一圈
(1)已知 ,你能求出满足条件的角 吗?
已知正弦值求角.
y
o
x
2个?
×
…
…
无数个
问题:方程有几个解?怎样表达?
解的分类:终边与 重合
终边与 重合
(1)已知 ,你能求出满足条件的角 吗?
已知正弦值求角.
y
o
x
… 、 、 、…
… 、 、 、…
终边相同的角
三角函数值相等
相差整数个 .
问题:方程有几个解?怎样表达?
解的分类:终边与 重合
终边与 重合
(1)已知 ,你能求出满足条件的角 吗?
已知正弦值求角.
y
o
x
解:(1)因为,在 内
所以, 的取值集合是
(1)已知 ,你能求出满足条件的角 吗?
已知正弦值求角.
y
o
x
(2)已知 ,你能求出 的取值范围吗?
已知正弦值的范围,求角的范围.
角的终边的区域
点P的区域
纵坐标的范围
形
视角一:
三角函数定义
单位圆
角 值的范围
正弦值的范围
数
求
对 应
对 应
确定
确定
y
o
x
(2)已知 ,你能求出 的取值范围吗?
已知正弦值的范围,求角的范围.
y
o
x
角的终边的区域
点P的区域
纵坐标的范围
视角一:
三角函数定义
单位圆
确定
确定
(包括边界)
形
(2)已知 ,你能求出 的取值范围吗?
已知正弦值的范围,求角的范围.
y
o
x
视角一:
三角函数定义
单位圆
数
形
解:(2)因为,在 内,
当 时,
所以,在 上 的取值集合是
(2)已知 ,你能求出 的取值范围吗?
已知正弦值的范围,求角的范围.
y
o
x
方程 的解
不等式 的解集
函数 图像上函数值等于a的点的横坐标
函数 与
图像交点的横坐标
函数 图像上纵坐标大于等于a的点横坐标集合
函数 位于 图像上方(含交点)的点横坐标集合
已知正弦值(范围),求角的值(范围).
视角二:
三角函数
方程
不等式
函数
(不等号也可以是<、≤、>)
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
分析:
已知正弦值(范围),求角的值(范围).
视角二:
三角函数的性质与图像
相差
相差
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
已知正弦值(范围),求角的值(范围).
解:(1)因为,在 内
所以, 的取值集合是
相差
相差
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
分析:
已知正弦值(范围),求角的值(范围).
视角二:
三角函数的性质与图像
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
已知正弦值(范围),求角的值(范围).
解:(2)因为,在 内,
当 时,
所以,在 上 的取值集合是
已知三角函数值求角
正弦函数图像
步骤
一个周期内
定义域内
依据
三角函数定义
y
o
x
已知正弦值(范围),求角的值(范围).
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
已知正弦值(范围),求角的值(范围).
(1)
(2)
对解的再认识
已知正弦值(范围),求角的值(范围).
y
o
x
视角一:
三角函数定义
单位圆
视角二:
三角函数的性质和图像
已知正弦值(范围),求角的值(范围).
y
o
x
视角二:
三角函数的性质和图像
视角一:
三角函数定义
单位圆
已知正弦值(范围),求角的值(范围).
y
o
x
视角一:
三角函数定义
单位圆
视角二:
三角函数的性质和图像
分析:
例1 已知 ,求角 .
已知余弦值(范围),求角的值(范围).
o
角的终边
点P
横坐标
余弦值
数
形
角 值
分析:
例1 已知 ,求角 .
已知余弦值(范围),求角的值(范围).
o
角的终边
点P
横坐标
余弦值
数
形
角 值
解:因为 ,
或
所以,在 上 的取值集合是
例1 已知 ,求角 .
已知余弦值(范围),求角的值(范围).
o
若 ,求角 的取值范围.
已知余弦值(范围),求角的值(范围).
o
解:
×
解:当 时,
解得
的取值集合是
若 ,求角 的取值范围.
已知余弦值(范围),求角的值(范围).
o
余弦函数图像
若已知 , 求角 .
已知余弦值(范围),求角的值(范围).
o
思路一:
思路二:
的取值集合.
取值范围.
的取值集合.
所以当 时,
解:因为 或
所以
又因为 ,
所以, 的取值集合是
若已知 , 求角 .
已知余弦值(范围),求角的值(范围).
o
分析:
已知正切值(范围),求角的值(范围).
例2 若已知 ,求角 .
y
o
x
角的终边
点P
纵比横
正切值
数
形
角 值
解:因为 ,
又由
所以 的取值集合是
还可以得到 的解集是
若已知 ,求角 .
已知正切值(范围),求角的值(范围).
正切函数图像
y
o
x
所以,
可知,
满足 的 的取值集合是
满足 的 的取值集合是
已知正切值(范围),求角的值(范围).
思 想
三角函数定义
已知三角函数值求角
三角函数图像
步骤
数形结合
小结:
y
o
x
一个周期内
定义域内
依据
整体求解
方 法
(1) ;
作业:
1.求满足下列条件时 的取值集合.
(2) ;
(3) ;
(4) .
(1) ;
作业:
2.求满足下列条件时 的取值集合.
(2) ;
(3) ;
(4) .
(1)
作业:
3.求满足下列条件时 的取值集合.
(2)
高一年级 数学
已知三角函数值求角
问题:已知三角函数值或值的范围,如何求角的值或角的范围?
角
三角函数值
?
(1)已知 ,你能求出满足条件的角 吗?
(2)已知 ,你能求出 的取值范围吗?
问题:可以直接运算求解吗?
用哪些知识和方法来解决这类问题?
尝试与发现
(1)已知 ,你能求出满足条件的角 吗?
(2)已知 ,你能求出 的取值范围吗?
尝试与发现
三角函数定义
坐标系中的角
角的三角函数值
分析:
正弦函数
自变量
函数值
视角一:
视角二:
y
o
x
问题:已知三角函数值或值的范围,求角的值或角的范围.
角的终边
点位置
纵坐标
横坐标
纵比横
视角一:
三角函数定义
单位圆
问题:已知三角函数值或值的范围,求角的值或角的范围.
函数
方程
不等式
(不等号也可以是<、≤、>)
视角二:
三角函数的性质与图像
问题:坐标系中哪些信息对应 中的x与y?
角的终边
点P
纵坐标
角 值
正弦值
数
形
视角一:
三角函数定义
单位圆
对 应
对 应
y
o
x
已知三角函数值或值的范围,求角的值或角的范围.
问题:随着角的终边的旋转,正弦值是怎样变化的?
视角一:
三角函数定义
单位圆
在 内,
在 内,
……
x
y
o
已知三角函数值或值的范围,求角的值或角的范围.
问题:已知正弦值求角的思维路径.
已知正弦值求角.
角的终边
点P
纵坐标
角 值
正弦值
数
形
视角一:
三角函数定义
单位圆
x
y
o
求
对 应
对 应
确定
确定
问题:方程有几个解?怎样表达?
逆时针旋转一圈
顺时针旋转一圈
(1)已知 ,你能求出满足条件的角 吗?
已知正弦值求角.
y
o
x
2个?
×
…
…
无数个
问题:方程有几个解?怎样表达?
解的分类:终边与 重合
终边与 重合
(1)已知 ,你能求出满足条件的角 吗?
已知正弦值求角.
y
o
x
… 、 、 、…
… 、 、 、…
终边相同的角
三角函数值相等
相差整数个 .
问题:方程有几个解?怎样表达?
解的分类:终边与 重合
终边与 重合
(1)已知 ,你能求出满足条件的角 吗?
已知正弦值求角.
y
o
x
解:(1)因为,在 内
所以, 的取值集合是
(1)已知 ,你能求出满足条件的角 吗?
已知正弦值求角.
y
o
x
(2)已知 ,你能求出 的取值范围吗?
已知正弦值的范围,求角的范围.
角的终边的区域
点P的区域
纵坐标的范围
形
视角一:
三角函数定义
单位圆
角 值的范围
正弦值的范围
数
求
对 应
对 应
确定
确定
y
o
x
(2)已知 ,你能求出 的取值范围吗?
已知正弦值的范围,求角的范围.
y
o
x
角的终边的区域
点P的区域
纵坐标的范围
视角一:
三角函数定义
单位圆
确定
确定
(包括边界)
形
(2)已知 ,你能求出 的取值范围吗?
已知正弦值的范围,求角的范围.
y
o
x
视角一:
三角函数定义
单位圆
数
形
解:(2)因为,在 内,
当 时,
所以,在 上 的取值集合是
(2)已知 ,你能求出 的取值范围吗?
已知正弦值的范围,求角的范围.
y
o
x
方程 的解
不等式 的解集
函数 图像上函数值等于a的点的横坐标
函数 与
图像交点的横坐标
函数 图像上纵坐标大于等于a的点横坐标集合
函数 位于 图像上方(含交点)的点横坐标集合
已知正弦值(范围),求角的值(范围).
视角二:
三角函数
方程
不等式
函数
(不等号也可以是<、≤、>)
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
分析:
已知正弦值(范围),求角的值(范围).
视角二:
三角函数的性质与图像
相差
相差
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
已知正弦值(范围),求角的值(范围).
解:(1)因为,在 内
所以, 的取值集合是
相差
相差
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
分析:
已知正弦值(范围),求角的值(范围).
视角二:
三角函数的性质与图像
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
已知正弦值(范围),求角的值(范围).
解:(2)因为,在 内,
当 时,
所以,在 上 的取值集合是
已知三角函数值求角
正弦函数图像
步骤
一个周期内
定义域内
依据
三角函数定义
y
o
x
已知正弦值(范围),求角的值(范围).
(1)已知 ,求满足条件的角 .
(2)已知 ,求 的取值范围.
已知正弦值(范围),求角的值(范围).
(1)
(2)
对解的再认识
已知正弦值(范围),求角的值(范围).
y
o
x
视角一:
三角函数定义
单位圆
视角二:
三角函数的性质和图像
已知正弦值(范围),求角的值(范围).
y
o
x
视角二:
三角函数的性质和图像
视角一:
三角函数定义
单位圆
已知正弦值(范围),求角的值(范围).
y
o
x
视角一:
三角函数定义
单位圆
视角二:
三角函数的性质和图像
分析:
例1 已知 ,求角 .
已知余弦值(范围),求角的值(范围).
o
角的终边
点P
横坐标
余弦值
数
形
角 值
分析:
例1 已知 ,求角 .
已知余弦值(范围),求角的值(范围).
o
角的终边
点P
横坐标
余弦值
数
形
角 值
解:因为 ,
或
所以,在 上 的取值集合是
例1 已知 ,求角 .
已知余弦值(范围),求角的值(范围).
o
若 ,求角 的取值范围.
已知余弦值(范围),求角的值(范围).
o
解:
×
解:当 时,
解得
的取值集合是
若 ,求角 的取值范围.
已知余弦值(范围),求角的值(范围).
o
余弦函数图像
若已知 , 求角 .
已知余弦值(范围),求角的值(范围).
o
思路一:
思路二:
的取值集合.
取值范围.
的取值集合.
所以当 时,
解:因为 或
所以
又因为 ,
所以, 的取值集合是
若已知 , 求角 .
已知余弦值(范围),求角的值(范围).
o
分析:
已知正切值(范围),求角的值(范围).
例2 若已知 ,求角 .
y
o
x
角的终边
点P
纵比横
正切值
数
形
角 值
解:因为 ,
又由
所以 的取值集合是
还可以得到 的解集是
若已知 ,求角 .
已知正切值(范围),求角的值(范围).
正切函数图像
y
o
x
所以,
可知,
满足 的 的取值集合是
满足 的 的取值集合是
已知正切值(范围),求角的值(范围).
思 想
三角函数定义
已知三角函数值求角
三角函数图像
步骤
数形结合
小结:
y
o
x
一个周期内
定义域内
依据
整体求解
方 法
(1) ;
作业:
1.求满足下列条件时 的取值集合.
(2) ;
(3) ;
(4) .
(1) ;
作业:
2.求满足下列条件时 的取值集合.
(2) ;
(3) ;
(4) .
(1)
作业:
3.求满足下列条件时 的取值集合.
(2)
